Презентація на тему:
Узагальнення та систематизація вивченого про іменник

Теорема Піфагора Виконала учениця 8-Б класу Шишка Софія

Геометрія володіє двома скарбами: один з них — це теорема Піфагора… Йоганн Кеплер

Піфагор Піфагор Самоський (570 – 496 рр. до н. е.) — давньогрецький філософ, математик, релігійний та політичний діяч. Піфагор є засновником в Кротоні (Південна Італія) Піфагорійської школи, яка поклала початок математичних наук. Крім математики, Піфагорійці займалися філософією, астрономією та теорією музики. До заслуг Піфагора належить відкриття та доведення теореми Піфагора.

Про теорему Піфагора Теорема Піфагора — одна із найвизначніших теорем математики, яка встановлює співвідношення між сторонами прямокутного трикутника. З неї або з її допомогою можна вивести більшість теорем. Вона застосовується в геометрії практично на кожному кроці. Відомо, що ця теорема не була відкрита Піфагором. Однак саме Піфагор першим дав її повноцінне доведення. На даний момент в науковій літературі зафіксовано кілька сотень доведень даної теореми.

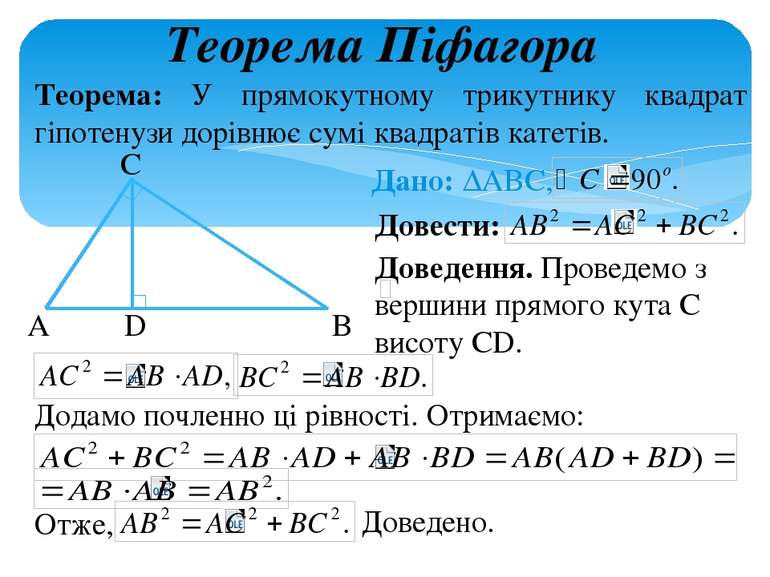
Теорема Піфагора Теорема: У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Довести: Доведення. Проведемо з вершини прямого кута С висоту СD. Додамо почленно ці рівності. Отримаємо: Отже, Доведено. Дано: ∆ABC, A C B D

Алгебраїчне доведення Розташуємо чотири однакові прямокутні трикутники так, як це зображено на малюнку. Чотирикутник зі сторонами c є квадратом, оскільки сума двох гострих кутів 90* , а розгорнутий кут —180* . Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною «a+b», а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.

можна отримати наступні формули: Якщо a, b — катети прямокутного трикутника, а с — його гіпотенуза, то з формули За цими формулами за двома будь-якими сторонами прямокутного трикутника знаходимо його третю сторону. с

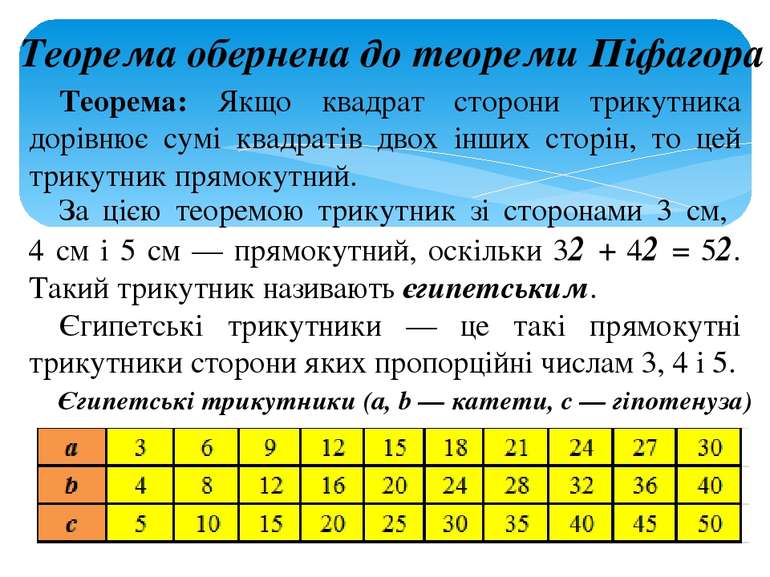
Теорема обернена до теореми Піфагора Теорема: Якщо квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін, то цей трикутник прямокутний. За цією теоремою трикутник зі сторонами 3 см, 4 см і 5 см — прямокутний, оскільки 32 + 42 = 52. Такий трикутник називають єгипетським. Єгипетські трикутники — це такі прямокутні трикутники сторони яких пропорційні числам 3, 4 і 5. Єгипетські трикутники (a, b — катети, c — гіпотенуза)

Старовинні задачі Задача індійського математика XII століття Бхаскари На березі ріки росла самотня тополя. Раптом налетіли вітри і зламали її стовбур. Бідна тополя впала, утворивши кут між стовбуром і поверхнею води річки. Запам'ятай тепер, що в цьому місці річка У чотири лише фута була шириною. Верхівка зламалася, залишивши всього три фути від усього стовбура. Прошу тебе, швидко тепер мені скажи: «Яка за велика в тополі висота?» Розв’язання (футів) 1 фут = 0,3048 м, тому AB=1,524 м.

Дякую за увагу