Презентація на тему:
Упровадження діяльнісного методу навчання у викладання математики на основі сучасних інформаційних технологій
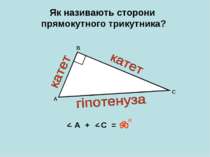
Завантажити презентацію
Упровадження діяльнісного методу навчання у викладання математики на основі сучасних інформаційних технологій
Завантажити презентаціюПрезентація по слайдам:
Семінар учителів математики шкіл Святошинського району та слухачів курсів підвищення кваліфікації при КМПУ ім. Б.Д. Грінченка «Упровадження діяльнісного методу навчання у викладання математики на основі інформаційних технологій» Спеціалізована школа №185 Святошинського району м. Києва 17 лютого 2009 року
Вступне слово до учасників семінару Гуменна Ольга Миколаївна, методист науково-методичного центру Святошинського РУО
Дидактична система діяльнісного методу навчання Кузькова Тетяна Петрівна, заступник директора школи з науково-методичної роботи
Засвоюємо: 10% того, що читаємо 20% того, що чуємо 30% того, що бачимо 50% того, що бачимо і чуємо 70% того, що говоримо 90% того, що говоримо і робимо
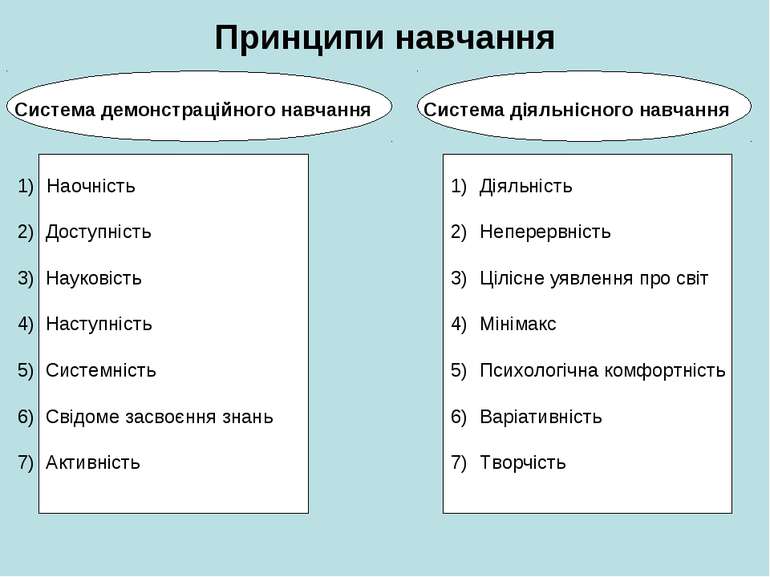
Принципи навчання Система демонстраційного навчання Система діяльнісного навчання Наочність 2) Доступність 3) Науковість 4) Наступність 5) Системність 6) Свідоме засвоєння знань 7) Активність Діяльність Неперервність Цілісне уявлення про світ Мінімакс Психологічна комфортність Варіативність Творчість
Підготовка уроку за технологією діяльнісного методу Гонтаренко Ігор Володимирович, голова методичного об’єднання вчителів математики СШ №185
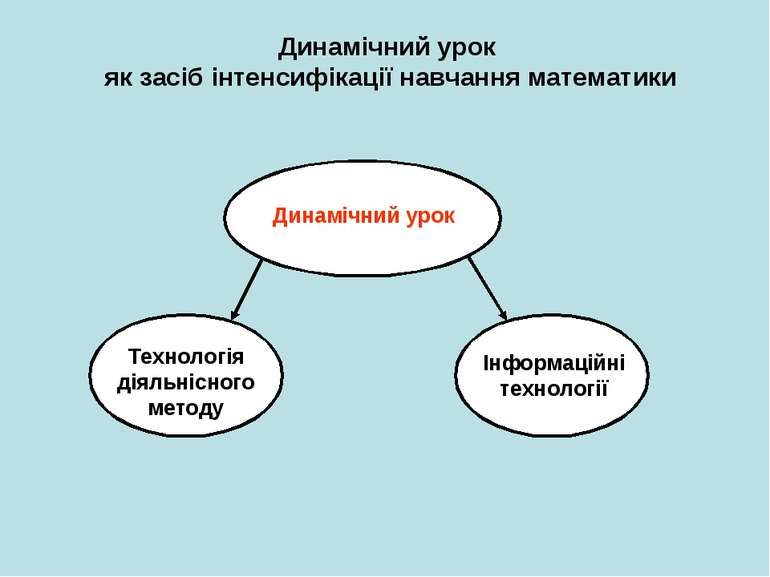
Динамічний урок як засіб інтенсифікації навчання математики Динамічний урок Технологія діяльнісного методу Інформаційні технології
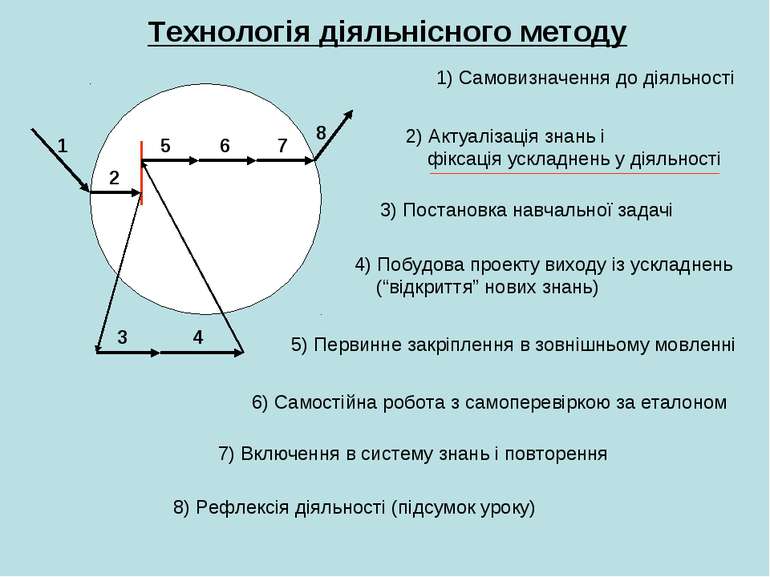
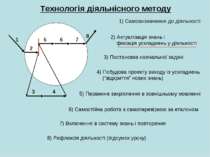
Технологія діяльнісного методу 1 2 3 4 5 6 7 8 1) Самовизначення до діяльності 2) Актуалізація знань і фіксація ускладнень у діяльності 3) Постановка навчальної задачі 4) Побудова проекту виходу із ускладнень (“відкриття” нових знань) 5) Первинне закріплення в зовнішньому мовленні 6) Самостійна робота з самоперевіркою за еталоном 7) Включення в систему знань і повторення 8) Рефлексія діяльності (підсумок уроку)
Підготовка уроку за технологією діяльнісного методу 1) Вибір теми, визначення мети (календарний план, програма) 2) Аналіз навчального матеріалу з обраної теми за наявними в дітей підручниками: - основні теоретичні та інформаційні відомості (означення, логічні висновки, твердження та інше); - практичне застосування матеріалу (проблеми, приклади, задачі) 3) Побудова діалогу з висновками про основне теоретичне посилання уроку та фіксування питань для актуалізації 4) Побудова діалогу щодо практичного використання основного теоретичного посилання та фіксування питань для актуалізації 5) Підготовка завдань для самостійної роботи та еталону для її самоперевірки 6) Підготовка завдання, де новий матеріал використовується як крок в більш загальному алгоритмі вирішення проблеми (задачі та інше) 7) Складання завдань для актуалізації знань, умінь та навичок на основі зафіксованих питань і побудова ускладнення 8) Підготовка діалогу щодо самооцінки дітьми власної діяльності на уроці 9) Складання конспекту та електронної частини уроку
1) Вибір теми, визначення мети (календарний план, навчальна програма) Метричні співвідношення в прямокутному трикутнику
Аналіз та визначення навчального матеріалу з обраної теми за наявними в дітей підручниками: - основні теоретичні та інформаційні відомості (означення, логічні висновки, твердження та ін.); - практичне застосування матеріалу (проблеми, приклади, задачі) 1) Поняття проекції катета на гіпотенузу 2) Теорема про співвідношення в прямокутному трикутнику 3) Задача на висоту, проведену до гіпотенузи 4) Задача на катети 5) Комбінована задача на висоту і катети 6) Задача з трапецією та діагоналлю, перпендикулярною до бічної сторони 7) Задача з колом, де проведено перпендикуляр до діаметра
3) Побудова діалогу з висновками про основне теоретичне посилання уроку та фіксування питань для актуалізації
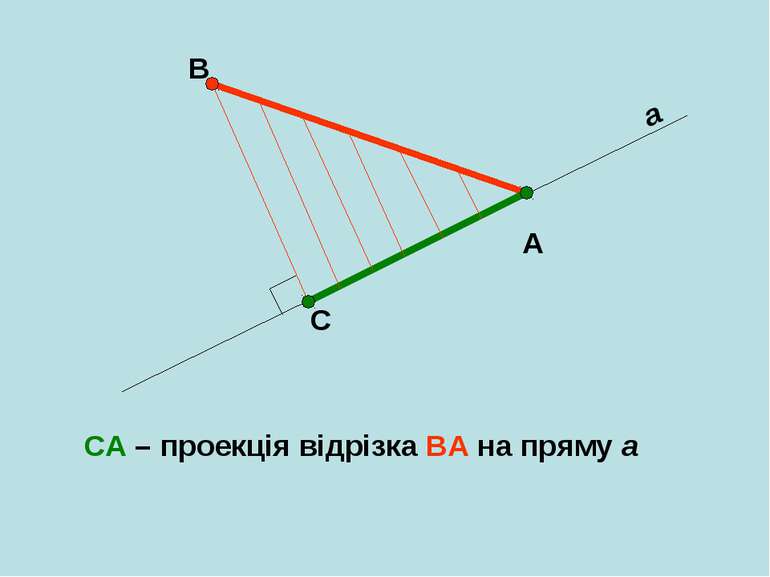
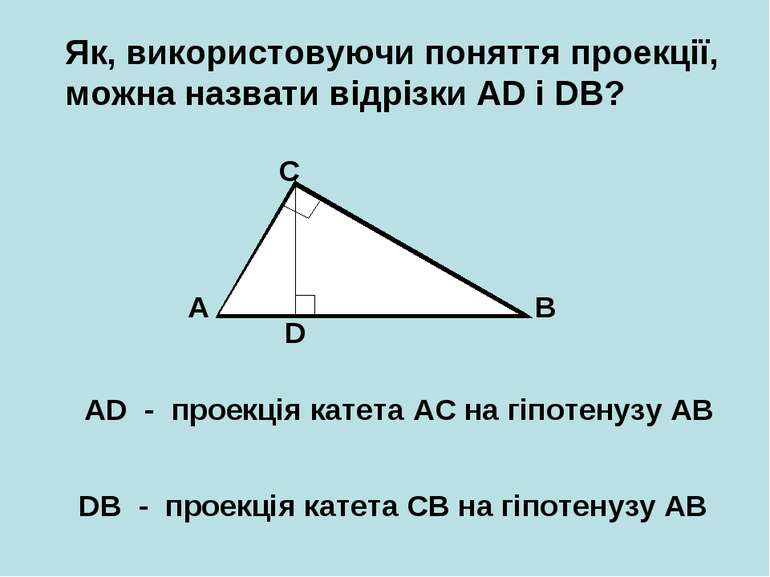
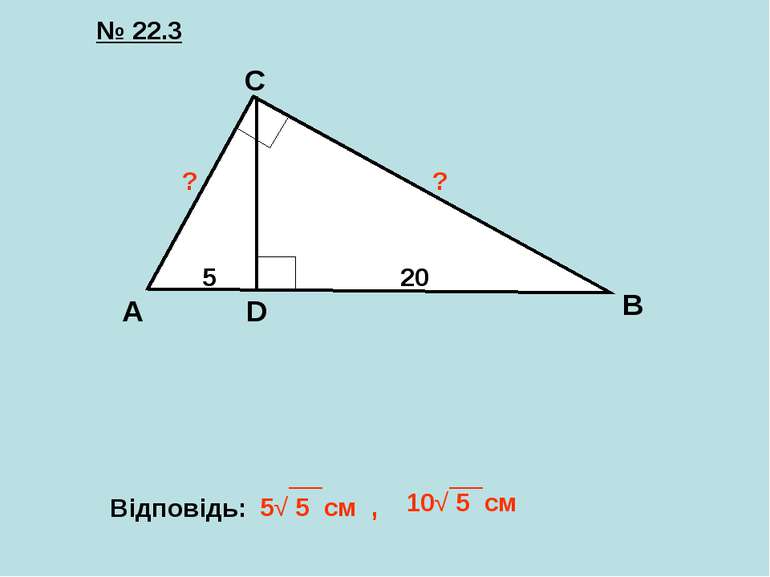
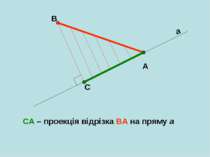
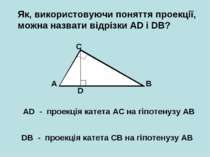
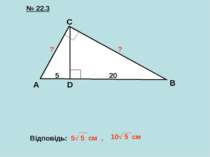
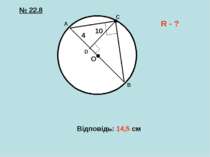
Як, використовуючи поняття проекції, можна назвати відрізки AD і DB? A B C D AD - проекція катета АС на гіпотенузу АВ DB - проекція катета СВ на гіпотенузу АВ
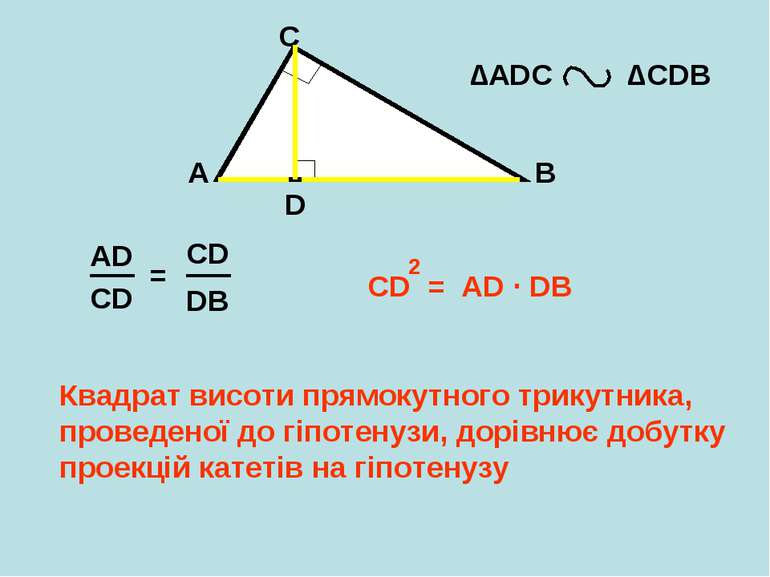
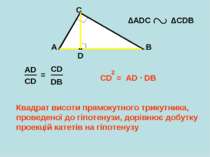
A B C D ∆АDС ∆CDB AD CD = CD = AD ∙ DB 2 Квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетів на гіпотенузу CD DB
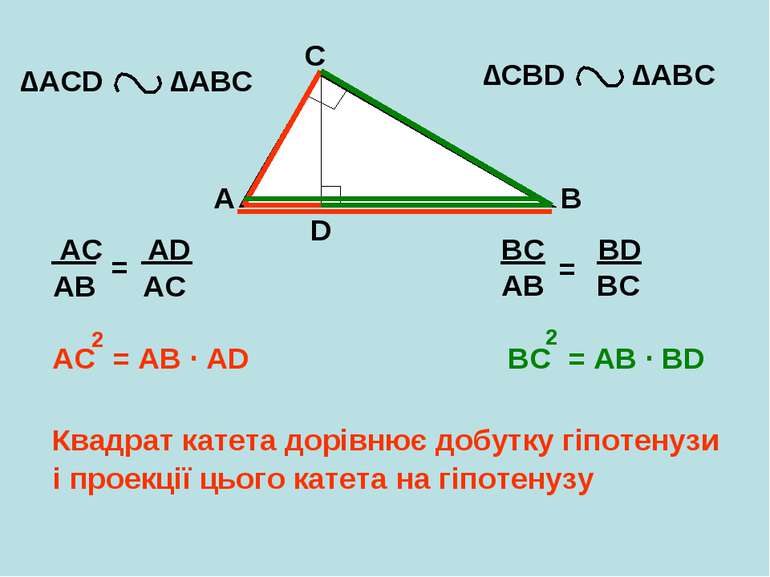
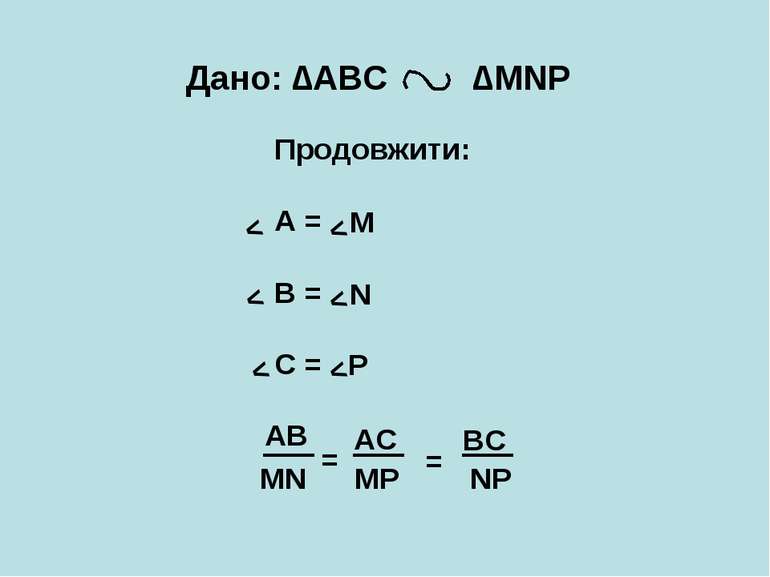
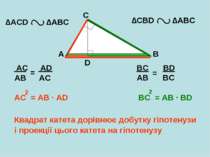
A B C D ∆АCD ∆АВС ∆CBD ∆АВС ВС = АВ BC = AB ∙ BD 2 AC = AB AC = AB ∙ AD 2 Квадрат катета дорівнює добутку гіпотенузи AD AC BD BC і проекції цього катета на гіпотенузу
4) Побудова діалогу щодо практичного використання основного теоретичного посилання та фіксування питань для актуалізації
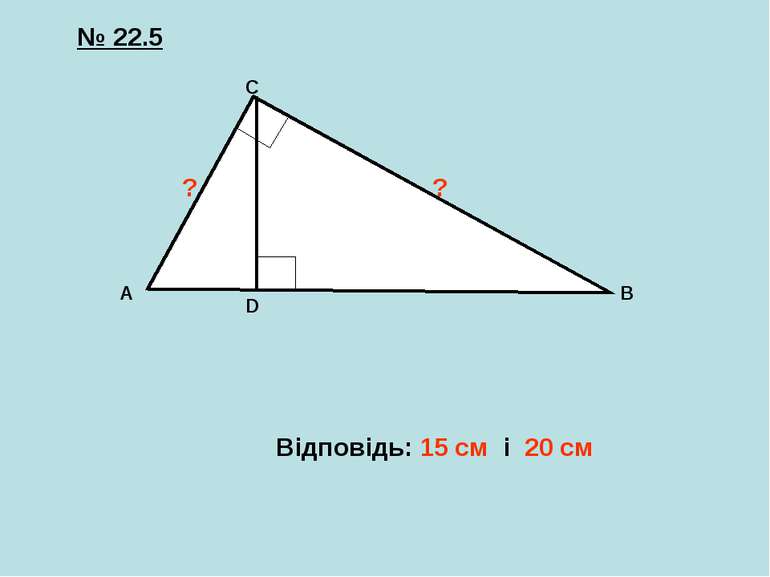
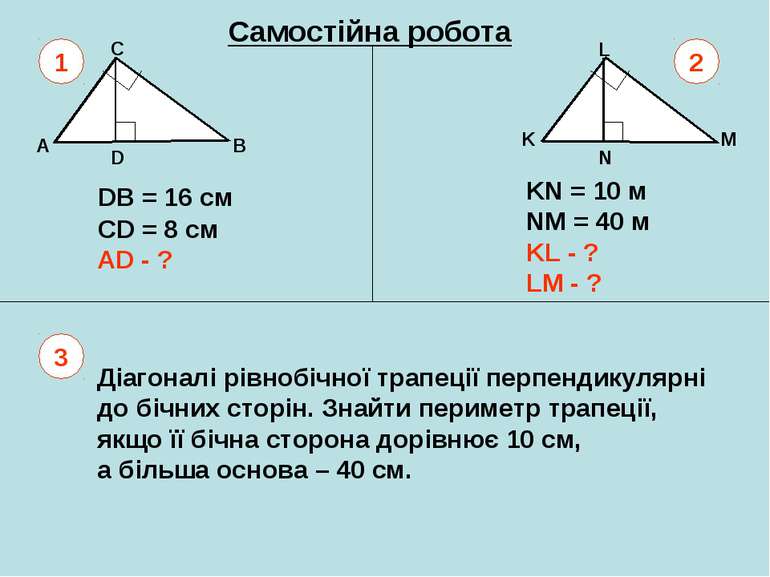
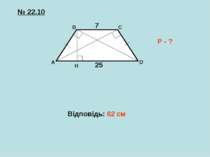
Самостійна робота A B C D K L M N DB = 16 см СD = 8 см AD - ? KN = 10 м NM = 40 м KL - ? LM - ? 1 2 3 Діагоналі рівнобічної трапеції перпендикулярні до бічних сторін. Знайти периметр трапеції, якщо її бічна сторона дорівнює 10 см, а більша основа – 40 см.
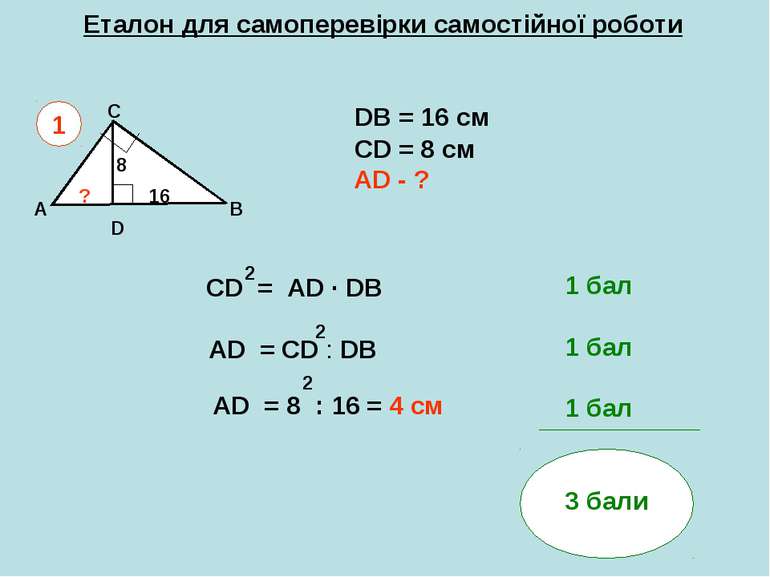
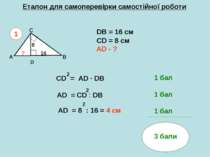
Еталон для самоперевірки самостійної роботи A B C DB = 16 см СD = 8 см AD - ? 1 D 8 16 ? CD = AD ∙ DB 2 AD = CD : DB 2 AD = 8 : 16 = 4 см 2 1 бал 1 бал 1 бал 3 бали
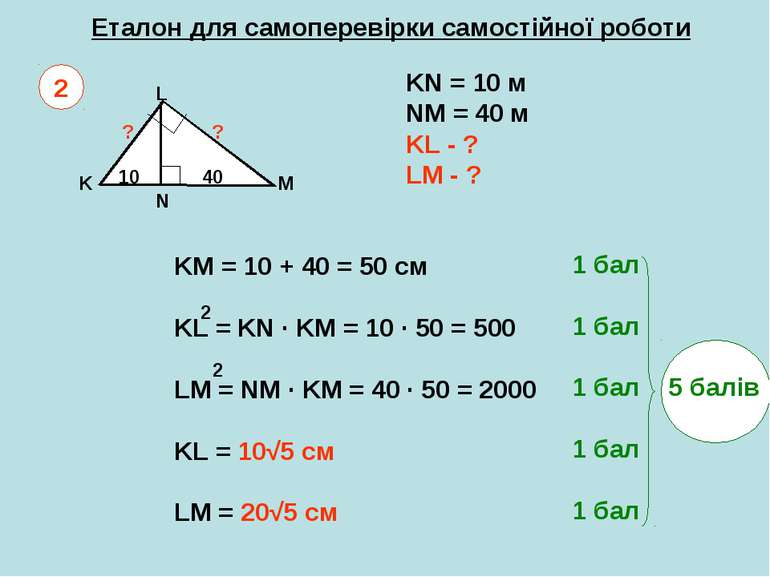
Еталон для самоперевірки самостійної роботи K L M N KN = 10 м NM = 40 м KL - ? LM - ? 2 10 40 ? ? KM = 10 + 40 = 50 см KL = KN · KM = 10 · 50 = 500 LM = NM · KM = 40 · 50 = 2000 KL = 10√5 см LM = 20√5 см 2 2 1 бал 1 бал 1 бал 5 балів 1 бал 1 бал
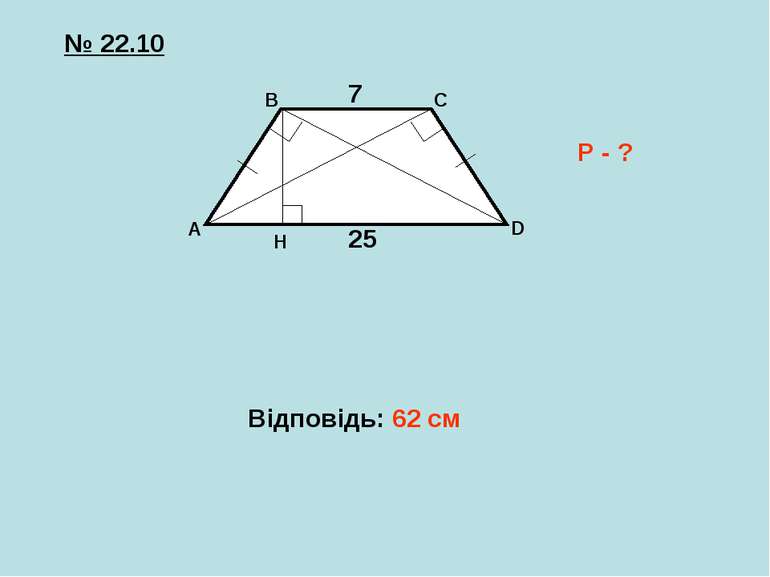
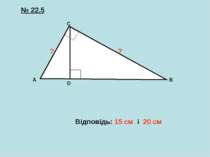
Еталон для самоперевірки самостійної роботи A B C D Н 10 3 10 40 AB = CD =10 см AD = 40 см Р - ? ABCD Проводимо ВН AD АВ = AD · AH AH = AB : AD = 100 : 40 = 2,5 см ВС = AD – 2AH = 40 – 5 = 35 см Р = 2АВ + AD + BC = 20 + 40 + 35 = 95 см ┴ ABCD 0,5 бала (малюнок) 0,5 бала 0,5 бала 0,5 бала 0,5 бала 0,5 бала 3 б. 2 2
6) Підготовка завдання, де новий матеріал використовується як крок у більш загальному алгоритмі вирішення проблеми
7) Складання завдань для актуалізації знань, умінь та навичок на основі зафіксованих питань і побудова ускладнення
Знайти значення змінної, якщо х – довжина сторони трикутника х 36 х 9 = х = 9 · 36 2 х = 18
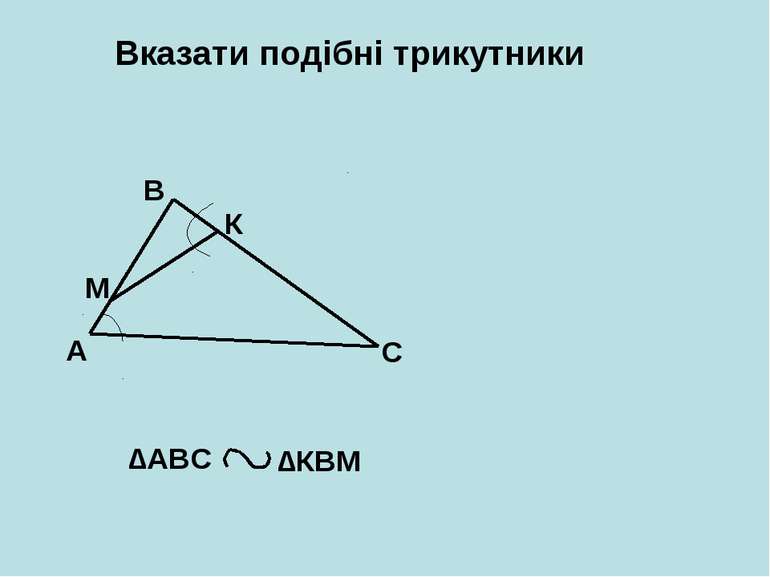
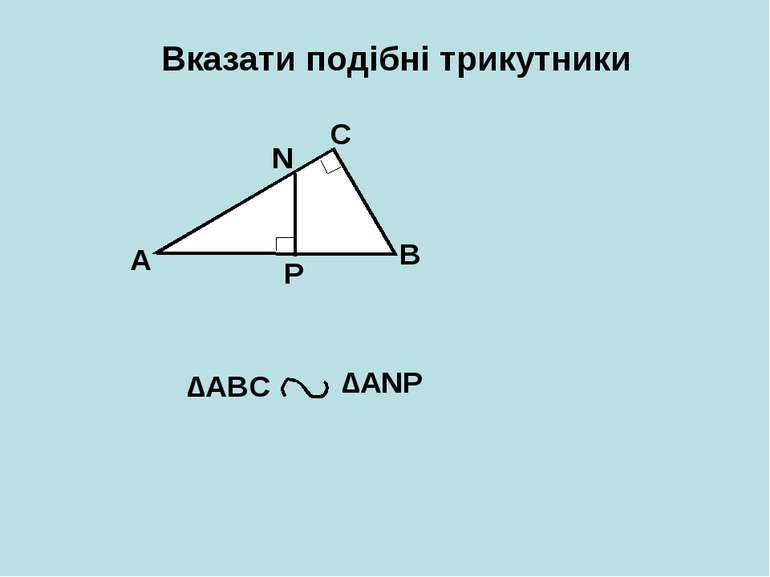
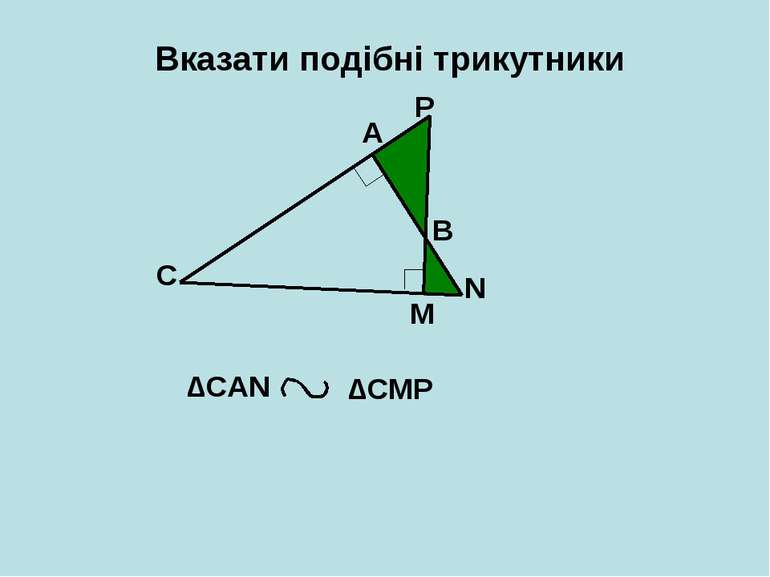
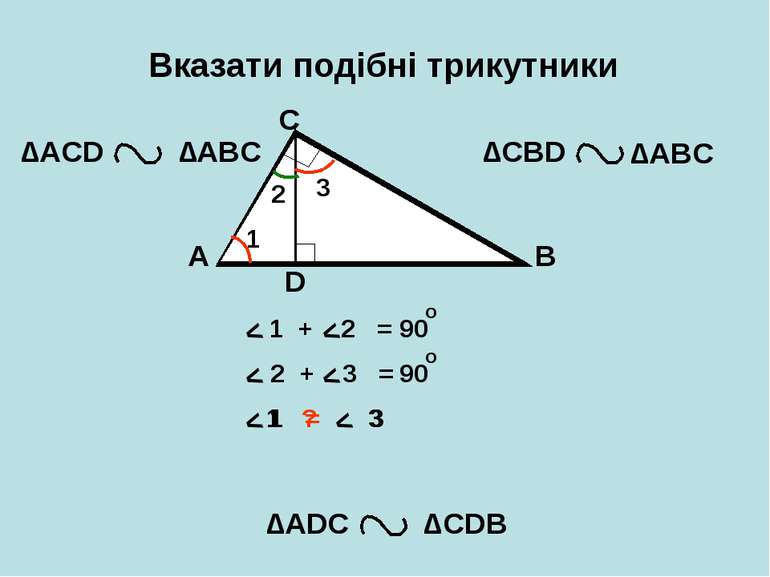
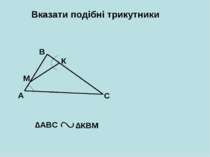
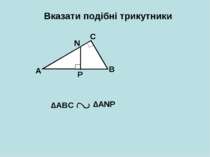
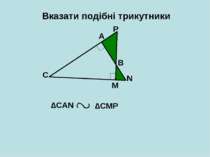
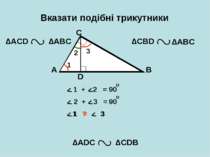
Вказати подібні трикутники A B C D ∆АCD ∆CBD ∆АDС ∆CDB ∆АВС ∆АВС 1 2 3 < < < < < < 1 + 2 = 2 + 3 = 1 ? 3 90 о 90 о 1 = 3
Схожі презентації
Категорії