Презентація на тему:
Елементи комбінаторики. Методика навчання

Елементи комбінаторики Методика навчання

Місце теми в програмі 5 – й клас В темі “Натуральні числа. Геометричні фігури і величини” передбачається розв'язування текстових, зокрема комбінаторних задач. 11 – клас Елементи комбінаторики

Мета вивчення теми (11 клас) Ввести поняття множини та її елементів, ознайомити з видами множини та операціями над ними. Навчити виконувати операції над множинами. Ввести означення впорядкованої множини, перестановки, розміщення і комбінації. Довести формули для обчислення числа кожного виду сполук. Навчити розрізняти види сполук і розв’язувати комбінаторні задачі

Зміст навчального матеріалу Множина та її елементи. /Числові множини N, Z, Q, R. Множина комплексних чисел./ Порожня множина. Способи задання множин. Підмножина даної множини. Об’єднання і переріз множин. Віднімання і доповнення множин. Упорядкована множина. Перестановки. Розміщення. Комбінації. Біном Ньютона. Розв’язування прикладних задач.

При цьому учні повинні мати уявлення про множину та її елементи; порожню множину; способи задання множин; підмножину даної множини; знати означення операцій над множинами; доповнення множини; впорядкованої множини; перестановки, розміщення і комбінації та формули для обчислення їх числа; уміти задавати множини; утворювати підмножини даної множини; знаходити результати операцій над множинами, доповнення множини; розрізняти види сполук і знаходити їх число за відповідними формулами; розв’язувати нескладні комбінаторні задачі.

Орієнтовне планування теми

Комбінаторні задачі Комбінаторика — розділ елементарної математики, в якому для скінченних множин розглядаються різні сполуки елементів, такі, як комбінації, розміщення, перестановки, а також усі ці види сполук з повтореннями та схожі поняття. Комбінаторні задачі — задачі вибору і розміщення елементів скінченної множини.

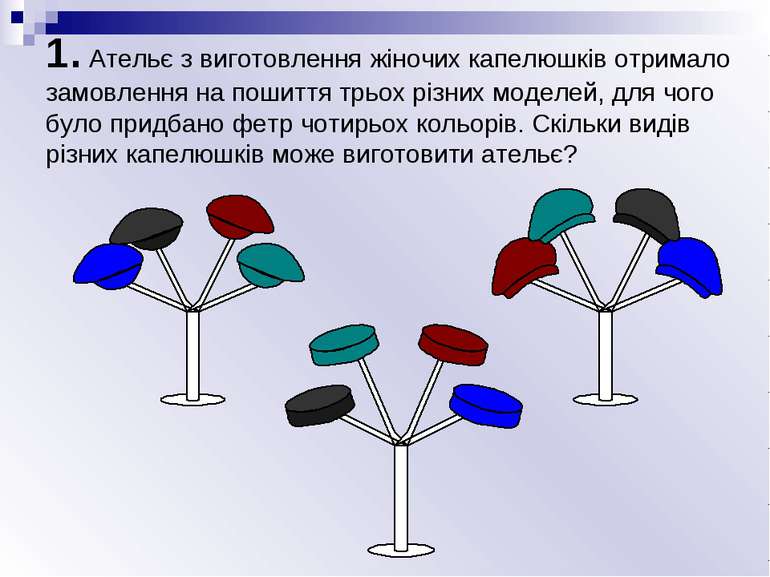
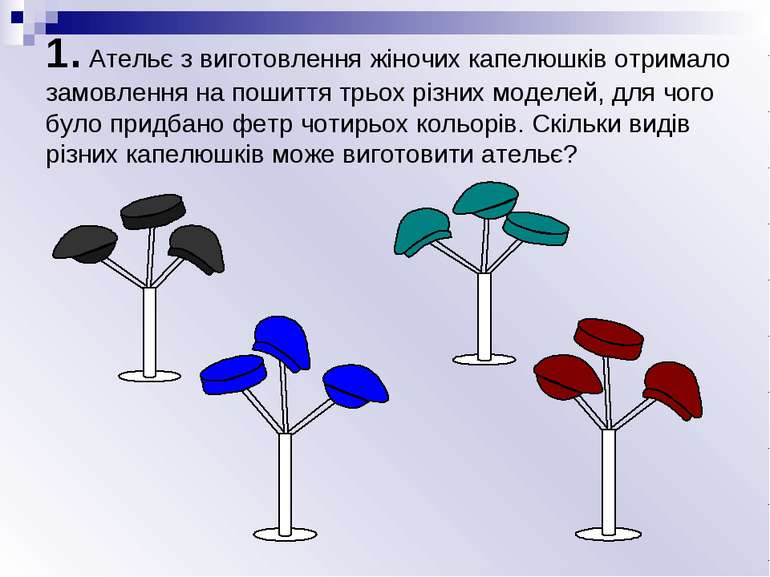
1. Ательє з виготовлення жіночих капелюшків отримало замовлення на пошиття трьох різних моделей, для чого було придбано фетр чотирьох кольорів. Скільки видів різних капелюшків може виготовити ательє?

1. Ательє з виготовлення жіночих капелюшків отримало замовлення на пошиття трьох різних моделей, для чого було придбано фетр чотирьох кольорів. Скільки видів різних капелюшків може виготовити ательє?

1. Ательє з виготовлення жіночих капелюшків отримало замовлення на пошиття трьох різних моделей, для чого було придбано фетр чотирьох кольорів. Скільки видів різних капелюшків може виготовити ательє?

1. Ательє з виготовлення жіночих капелюшків отримало замовлення на пошиття трьох різних моделей, для чого було придбано фетр чотирьох кольорів. Скільки видів різних капелюшків може виготовити ательє? Всього є 3 варіанти вибору моделі. Для кожної моделі є 4 варіанти вибору кольору. Отже, всього різних пар (модель, колір) буде 3 · 4 = 12.

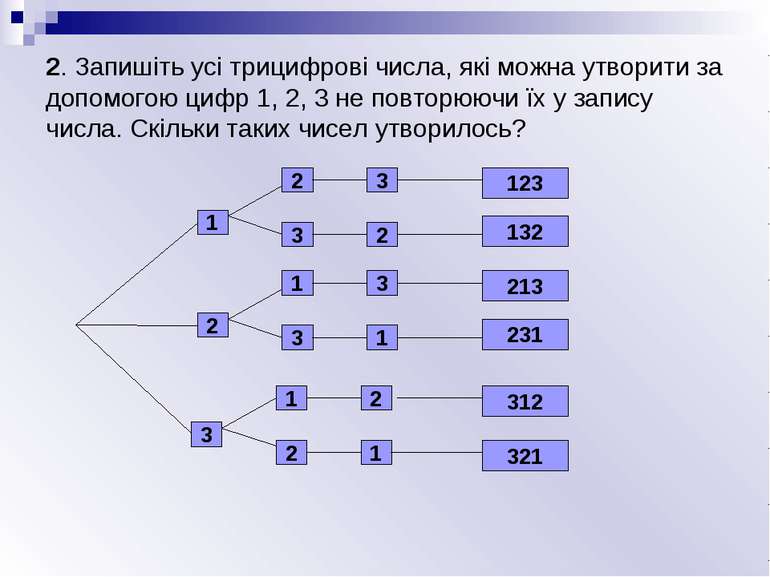
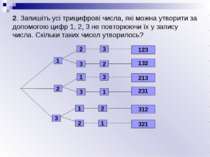
2. Запишіть усі трицифрові числа, які можна утворити за допомогою цифр 1, 2, 3 не повторюючи їх у запису числа. Скільки таких чисел утворилось? 1 2 3 2 3 1 3 1 2 3 2 3 1 2 1 123 132 213 231 312 321

2. Запишіть усі трицифрові числа, які можна утворити за допомогою цифр 1, 2, 3 не повторюючи їх у запису числа. Скільки таких чисел утворилось? На перше місце можна записати будь-яку з даних цифр, тобто є 3 різні можливості. На друге місце можна записати вже будь-яку з цифр, що лишилися, тобто є 2 можливості. Кожна перша цифра може комбінуватися з будь-якою цифрою, що стоїть на другому місці. Тому загальне число різних способів запису двох цифр є 3 2 = 6. Далі вже зрозуміло, що на третє місце можна записати вже тільки одну цифру, що залишились, тому для трьох цифр кількість способів є 3 2 1 = 6. 3. Як зміниться відповідь задачі 2, якщо цифру 3 замінити на цифру 0? Пояснити. Оскільки число не може починатися з цифри 0, то загальна кількість утворених чисел буде 2 2 1 = 4.

Комбінаторне правило множення Якщо деякий об’єкт А можна вибрати m способами і після кожного такого вибору інший об’єкт В можна вибрати (незалежно від вибору об’єкта А) n способами, то пару А і В можна вибрати m n способами.

4. Десять друзів зайшли перекусити до кав’ярні. Вони довго вирішували, яким чином розміститися за стійкою. Хазяїн кав’ярні запропонував їм угоду, за якою друзі можуть приходити щодня, але сідати кожного разу у різному порядку. Після того, як вони перепробують усі можливі варіанти, їх будуть годувати за рахунок закладу. На який день друзі отримають безкоштовний обід? Припустимо, що друзі заходять до кав’ярні по одному. Перший може вибрати собі місце 10 способами, другий — 9 способами. Тому для перших двох друзів є 10 · 9 = 90 варіантів зайняти два місця. Міркуючи аналогічно і застосовуючи правило множення, отримуємо 10 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = = 3 628 800 варіантів. У перерахунку на роки — більше 9935 років

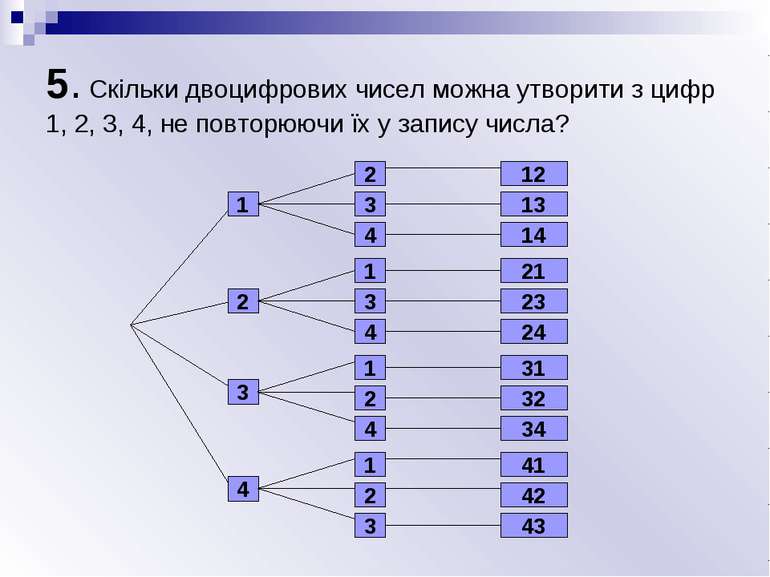
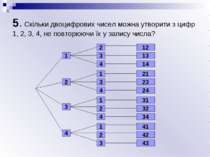
5. Скільки двоцифрових чисел можна утворити з цифр 1, 2, 3, 4, не повторюючи їх у запису числа? 1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3 12 13 14 21 23 24 31 32 34 41 42 43

5. Скільки двоцифрових чисел можна утворити з цифр 1, 2, 3, 4, не повторюючи їх у запису числа? Підрахунок кількості таких чисел можна виконати так. На перше місце можна вибрати будь-яку з 4-х цифр – всього 4 можливості. На друге місце – будь-яку з 3-х цифр, що залишилися – 3 можливості. Будь-яка цифра, що стоїть на першому місці може комбінуватися з будь-якою цифрою на другому місці. Тому загальне число різних способів за правилом множення є 4 3 = 12.

6. Скільки трицифрових чисел можна утворити з цифр 2, 3, 4, 7, не повторюючи цифри в запису числа? Як зміниться відповідь, якщо замість цифри 7 взяти цифру 0? 1) Міркуючи аналогічно задачі 4, отримаємо, що загальна кількість чисел є 4 3 2 = 24. 2) Якщо одна з цифр є 0, то на перше місце можна вибрати тільки одну з трьох цифр і тоді загальна кількість чисел є 3 3 2 = 18.

7. З 18 студентів групи необхідно вибрати старосту, його заступника і профорга. Скільки існує варіантів такого вибору? Першим можна вибрати старосту. Для цього є 18 можливостей. Для вибору його заступника залишається 17 можливостей. Для вибору профорга — 16. За правилом множення 18 17 16 = 4896

8. З тієї самої групи студентів (задача 7) необхідно вибрати трьох для участі у загально університетському заході. Скільки існує варіантів такого вибору? Можна міркувати аналогічно до розв’язання задачі 7, проте у виборі студентів для участі у заході порядок вибору несуттєвий, адже немає різниці між трійками «Петренко, Сидоренко і Іваненко» і «Сидоренко, Петренко і Іваненко» або «Іваненко, Сидоренко і Петренко». Тому шукана кількість трійок буде у стільки раз меншою від 4896 впорядкованих трійок, скільки раз можна упорядкувати одну трійку. Три елементи упорядкувати можна 3 · 2 · 1 = 6 способами. Отже, шукана кількість дорівнює 4896 : 6 = 816.

9. У продавця квітами є троянди 7 кольорів. Скільки можна утворити букетів з 5 різнокольорових троянд? Якщо враховувати порядок вибору троянд за кольором, то отримаємо 7 · 6 · 5 · 4 · 3 = 2520 варіантів. Але у букеті порядок вибору несуттєвий, тому всіх букетів буде

10. Ідучи на тренування спортсмен одягає або майку або футболку. Скільки варіантів вибору майки або футболки у нього є, якщо його мама випрала 3 майки і 4 футболки ? Припустимо, що у шафі на одній поличці лежать 3 майки, а на другій – 4 футболки. Довільно з якої-небудь полички беремо тільки одну річ. З першої полички взяти одну річ можна 3 різними способами, а з другої – 4 способами. Тоді взяти одну яку-небудь річ можна 3 + 4 = 7 різними способами.

Комбінаторне правило додавання Якщо деякий об’єкт А можна вибрати m способами, а об’єкт В можна вибрати іншими n способами, причому вибори об’єктів А і В несумісні, то вибір «або А або В» можна здійснити т + п способами.

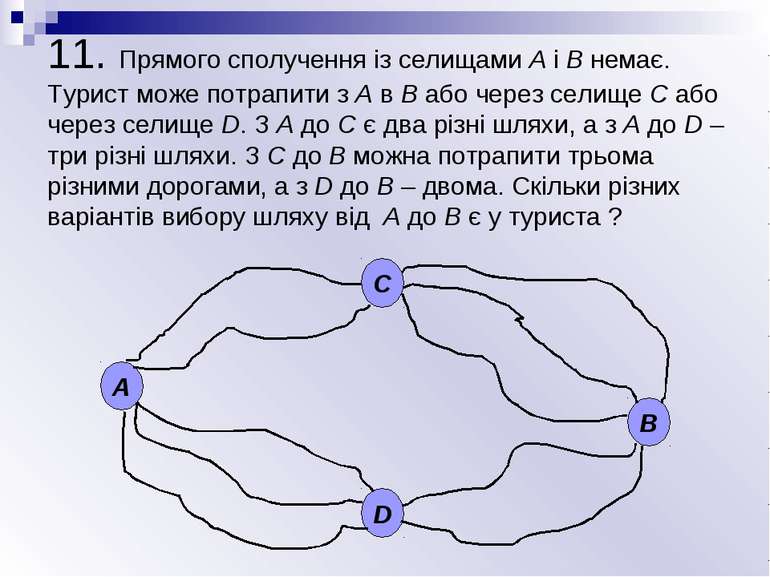
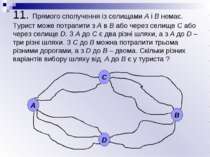
11. Прямого сполучення із селищами А і B немає. Турист може потрапити з А в В або через селище С або через селище D. З А до С є два різні шляхи, а з А до D – три різні шляхи. З С до В можна потрапити трьома різними дорогами, а з D до В – двома. Скільки різних варіантів вибору шляху від А до В є у туриста ? А С D В

11. Прямого сполучення із селищами А і B немає. Турист може потрапити з А в В або через селище С або через селище D. З А до С є два різні шляхи, а з А до D – три різні шляхи. З С до В можна потрапити трьома різними дорогами, а з D до В – двома. Скільки різних варіантів вибору шляху від А до В є у туриста ? Якщо йти з А в В через С, то за правилом множення шлях можна обрати 2 · 3 = 6 способами. Якщо йти з А в В через D , то для вибору шляху є 3 · 2 = 6 способів. Тоді різних варіантів вибору шляху за правилом додавання є 6 + 6 = 12.

Домашнє завдання Алгебра і початки аналізу: Підруч. для 11 кл.загальноосвіт. навч. закладів / М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук. – К.: Зодіак-ЕКО, 2003 Розв'язати №№ 110-113, 115-117, 120.

Дякую за увагу!