Презентація на тему:
Основні елементи комбінаторики

Тема: “ Основні елементи комбінаторики ” Підготували: Щур Х., Фощанко А., Король Л., Мацупа Н.

План Скінченні множини та операції над ними Предмет комбінаторики Перестановка Розміщення Сполучення

1. Скінчені множини та операції над ними В основі розповсюдженого теоретико-множинного методу викладання теорії ймовірностей лежить припущення, що кожному досліду поставлено у відповідність деяку множину елементів, які дають повну інформацію про можливі результати цього досліду. Всяка сукупність довільних елементів утворює множину. Множина вважається визначеною, якщо відомі всі її елементи. Якщо кількість елементів множини скінчена, то множина називається скінченою. Множини позначають великими латинськими літерами A, B,C тощо, а їх елементи відповідно малими літерами a,b,c... .

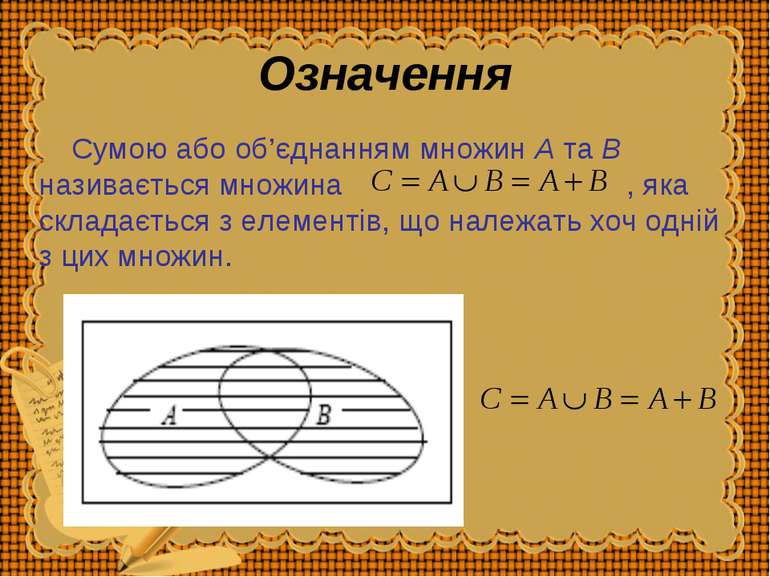
Означення Сумою або об’єднанням множин A та B називається множина , яка складається з елементів, що належать хоч одній з цих множин.

Приклад Нехай множина A складається з елементів 1,2,3, а множина B з елементів 2,3,4. Це записується: A ={1;2;3}, B ={2;3;4}. Тоді А+В= {1;2;3;4}

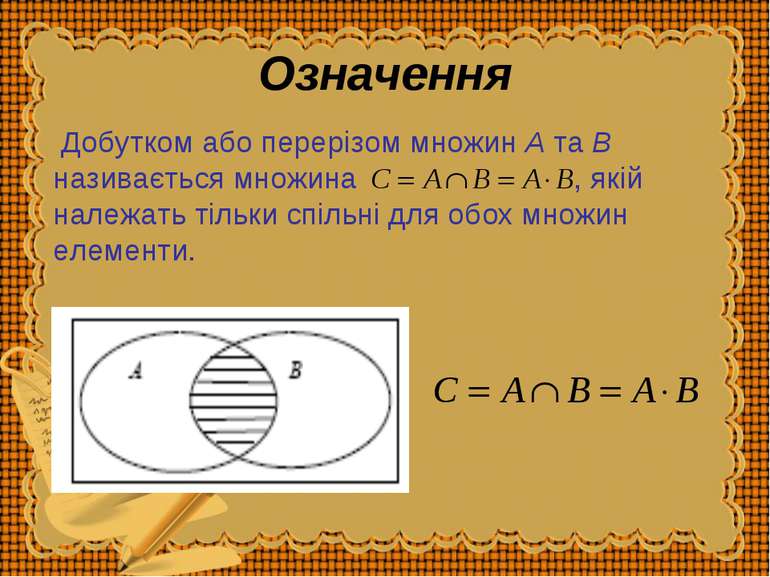
Означення Добутком або перерізом множин A та B називається множина , якій належать тільки спільні для обох множин елементи.

2. Предмет комбінаторики Комбінаторика – це розділ математики, в якому розглядаються задачі пов'язані з вибором та розташуванням елементів множини, основними елементами якої є: перестановка, сполучення (комбінація) та розміщення.

Теорема 1 Принцип суми: Якщо множина A містить n-елементів, а множина B - m елементів, і множини не перетинаються, то множина A B вміщує n + m елементів. Правило суми можна сформулювати ще й так: якщо вибір A можна здійснити n - способами, а вибір B − відповідно m - способами, то вибір A або B можна здійснити n + m способами.

Приклад Для проведення Олімпіади треба вибрати місто. У східній півкулі Землі запропоновано 5 міст, а в західній − 4. Скількома способами можна вибрати місто для проведення Олімпіади? Розв’язання: Вибір A (зі східної півкулі) можна здійснити 5-ма способами, а вибір B − 4-ма способами. Загальна кількість способів: 4 + 5 = 9 .

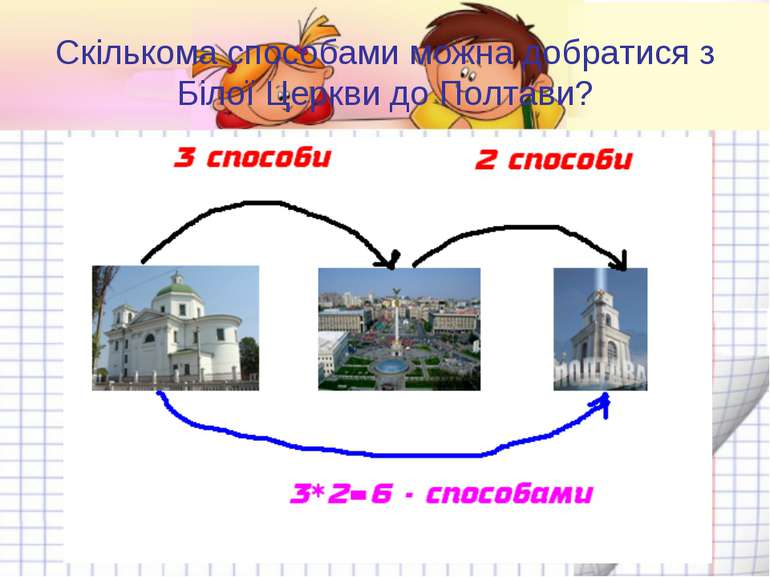
Теорема 2 Принцип добутку: Для множин та множина C всіх можливих пар з елементів обох множин містить n . m елементів і має вигляд: Сформулюємо це правило по-іншому. Якщо вибір A можна здійснити n-різними способами, і для кожного з цих способів вибір B можна здійснити m - способами, то вибір A і B можна здійснити n . m - способами.

Приклад З Білої Церкви до Києва можна добратися 3-ма видами транспорту (маршруткою, літаком або електричкою), а з Києва до Полтави 2-ма (поїздом або автобусом).

Скількома способами можна добратися з Білої Церкви до Полтави?

4.Перестановки Означення. Множини, для яких істотним є порядок розташування елементів, називаються упорядкованими. Дві упорядковані множини називаються рівними, якщо вони складаються з однакових і однаково розташованих елементів. Тому множини {a,b,c} і {b,c,a} − це різні упорядковані величини. Нехай скінчена упорядкована множина складається з n пронумерованих елементів. Будь-який спосіб розташування цих елементів складає результат дослідження.

Означення Перестановкою називається будь-яка впорядкована множина, яка складається з n елементів. Кількість таких перестановок Pn обчислюється за формулою: Pn = n!

Приклад Задана множина A ={1;2;3}. Знайти число перестановок. Розв’язання: З елементів множини чисел можемо отримати такі сполуки: 1,2,3 1,3,2 2,1,3 2,3,1 3,1,2 3,2,1, тобто число перестановок 3!= 1.2.3 =6. Таким чином, переставлення дають можливість знайти число способів порядкування множини, яка складається з n елементів. Для пустої множини (немає жодного елемента) існує єдиний спосіб упорядкування її, який вказує на існування пустої множини. Тому 0!=1.

4. Розміщення Розіб’ємо множину на упорядковані підмножини, які складаються з m елементів кожна, так щоб підмножини відрізнялись одна від другої або порядком розташування елементів, або самими елементами. Отримуємо певне розміщення елементів у підгрупах як результат досліду.

4. Розміщення Означеня: Розміщенням Anm з n елементів по m називається будь-яка впорядкована підмножина, що складається з m елементів, які вибрані з n елементів. Число можливих розміщеннь обраховується за формулою

Приклад Знайти число розміщень з 3-х елементів, заданих числами 1,2,3. Розв’язання: Розміщення з трьох елементів по два будуть: (1,2), (1,3), (2,1), (2,3), (3,1), (3,2). Розміщення (1,2) і (2,1) відрізняються лише порядком розташування елементів, тоді як розміщення (1,2) і (1,3) відрізняються самими елементами (хоч би одним):

5. Сполучення (комбінація) Означення: Розміщенням Сnm з n елементів по m називається будь-яка підмножина, що складається з m елементів, які вибрані з n елементів. Число можливих комбінацій обраховується за формулою

Приклад Скількома способами з 10 студентів можна вибрати 3-х на наукову конференцію? Розв'язання: Відомо, що всього студентів 10, тому n=10, потрібно вибрати 3-х, тому m=3, тоді: