Презентація на тему:
Планування експерименту при дисперсійному аналізі. Латинські і греко-латинські квадрати. Латинські куби

Доповідь на тему Планування експерименту при дисперсійному аналізі. Латинські і греко-латинські квадрати. Латинські куби

Планування експерименту при дисперсійному аналізі. В будь-якому експерименті середні значення досліджуваних величин змінюються у зв’язку зі зміною основних факторів (кількісних та якісних), що визначають умови досліду, а також і випадкових факторів. Дослідження впливу тих чи інших факторів на мінливість середніх є задачею дисперсійного аналізу. Дисперсійний аналіз особливо ефективний при вивченні кількох факторів. Експеримент в якому зустрічаються всі можливі комбінації факторів називається повним факторним експериментом. Експеримент в якому пропущені деякі комбінації рівнів, називається подрібнений факторний експеримент(ДФЕ). Скорочення перебору рівнів завжди призводить до втрати частини інформації. Тому при ДФЕ важливо так запланувати експеримент, щоб губилась найменш суттєва при даній постановці задачі інформація. Число дослідів можна значно скоротити, якщо скористатись ДФЕ по схемі латинського квадрату, використаного вперше Фішером.

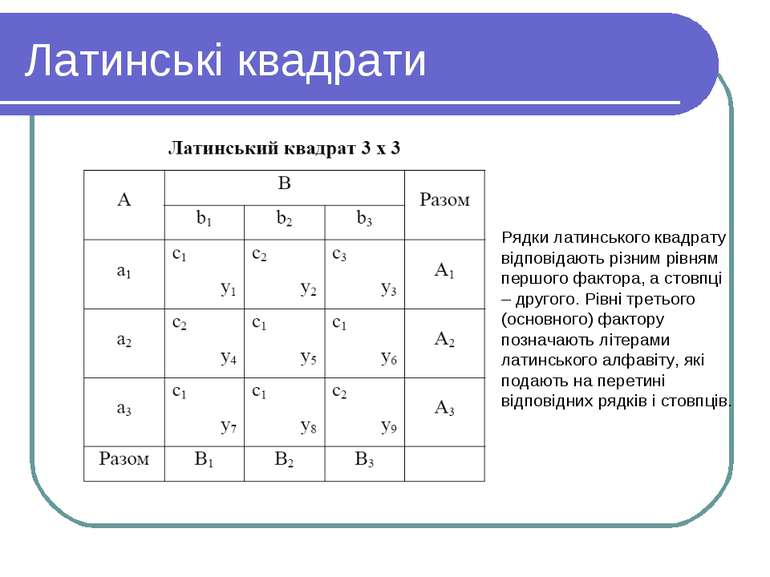
Латинські квадрати Латинський квадрат n x n – це квадратна таблиця, складена з n елементів (чисел чи букв) таким чином, що кожний елемент повторюється в кожній стрічці і кожному стовпчику тільки один раз. Рядки латинського квадрату відповідають різним рівням першого фактора, а стовпці – другого. Рівні третього (основного) фактору позначають літерами латинського алфавіту, які подають на перетині відповідних рядків і стовпців. Стандартні чи канонічні латинські квадрати - це такі квадрати, у яких перша стрічка та перший стовпець побудовані в алфавітному порядку (елементи квадрату – букви) чи в порядку натурального ряду (елементи квадрату – числа) [1]. Однокрокова циклічна перестановка в кінець стрічки – найбільш простий спосіб побудови латинського квадрату. Застосовуючи латинські квадрати, зазвичай, виходять з того, що ефекти взаємодії між факторами незначні. Тоді результати експерименту можна представити у вигляді лінійної моделі.

Латинські квадрати Рядки латинського квадрату відповідають різним рівням першого фактора, а стовпці – другого. Рівні третього (основного) фактору позначають літерами латинського алфавіту, які подають на перетині відповідних рядків і стовпців.

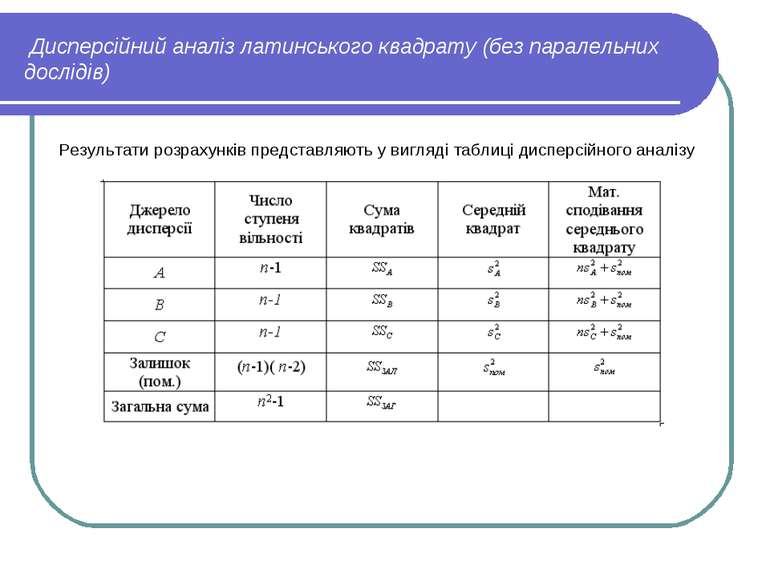
Латинські квадрати При проведенні дисперсійного аналізу латинського квадрату без повторних дослідів зручно користуватись наступним алгоритмом розрахунку. Для цього визначають: Суми по стрічках Аі, стовпцях Bj та латинських літерах Cq. Суму квадратів всіх дослідів Суму квадратів сум по стрічках, поділену на число спостережень в стрічці Суму квадратів сум по стовпцях, поділену на число спостережень в стовпці Суму квадратів сум по латинських буквах, поділену на число спостережень, що відповідає кожній букві Квадрат загальної суми, поділений на число всіх спостережень (коректуючий член) Суму квадратів для стрічки, стовпця та латинської букви Загальну суму квадратів, рівну різниці між сумою квадратів всіх спостережень та коректуючим членом Залишкову суму квадратів. Вона складається з дисперсії, обумовленої помилкою досліду, і дисперсії, обумовленої взаємодією факторів, якщо такі мають місце.

Дисперсійний аналіз латинського квадрату (без паралельних дослідів) Результати розрахунків представляють у вигляді таблиці дисперсійного аналізу

Греко – латинські квадрати Планування за латинським квадратом дозволяє ввести в дослідження три фактора. Для чотирьох факторів хороші властивості має план експерименту по схемі греко-латинського квадрату. Число рівнів для всіх факторів повинно бути однакове.

Греко – латинські квадрати В греко-латинських квадратах є n2 різких комбінацій рівнів факторів замість n4 комбінацій повного чотирифакторного експерименту. Тому греко Латинський квадрат являє собою 1/n2 репліку від ПФЕ. Дисперсійний аналіз греко-латинського квадрату проводять так само, як і аналіз звичайного латинського квадрата, з врахуванням четвертого фактора D. Основним припущенням, що лежить в основі застосування греко- латинських квадратів та квадратів вищих порядків, є припущення про відсутність взаємодії між факторами. Перевірити адекватність прийнятої лінійної моделі, як і при використанні латинських квадратів, можна тільки при наявності паралельних дослідів.

Латинські куби Повному факторному експерименту для трьох факторів n3 (n>2) відповідає кубічне розміщення з n елементів, що містить n3 позицій. Трьом ребрам кубу відповідають фактори А, В, С з рівнями 0, 1, 2, …, n-1. Коли ввести в план четвертий фактор D і рівні цього фактору (0, 1, 2, …, n-1) розмістити у відповідних до дослідів точках кубічного розміщення, то одержимо латинський куб розміру n першого порядку Планування експерименту по латинському кубу першого порядку дозволяє включити в розгляд чотири фактори (A, B, C i D). Відмінність від греко – латинського квадрату, котрий також дає можливість вивчити вплив чотирьох факторів є в тому, що в латинському кубі три фактори (A, B, C) рахуються головними і один фактор (D) складає елімінуюче групування, а в греко- латинському квадраті головними рахуються два фактори А та В, а C i D складають подвійне елімінуюче групування. Число дослідів в кубі в n раз більше, ніж в греко-латинському квадраті.