Презентація на тему:
"Діисні числа

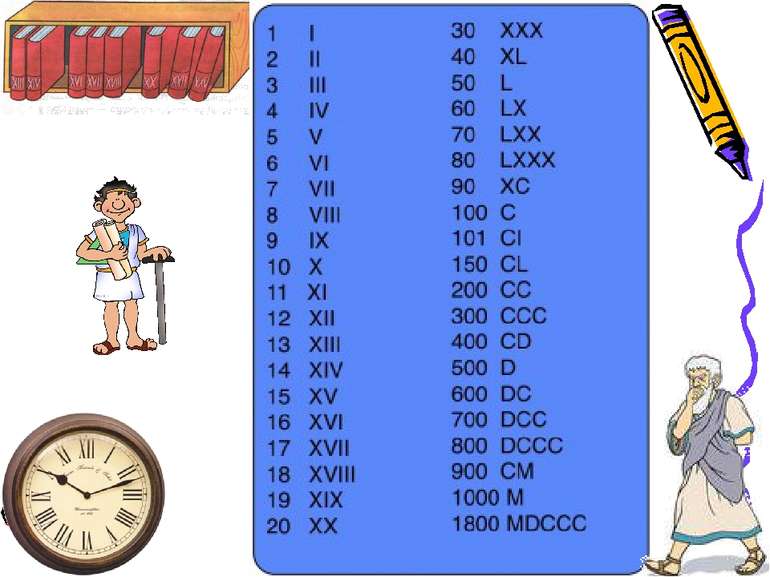
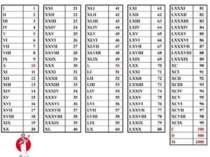
Дійсні числа Натуральні числа – це ті, які використовують при лічбі (натураль-ний ряд чисел є нескінченним: 1,2,3,4,5,…) 0 не є натуральним числом. Кожне натуральне число можна записати як суму розрядних доданків. 7 205 379 = 7 000 000 + 200 000 + 5000 + 300 +70 +9 Приклад: Приклад:

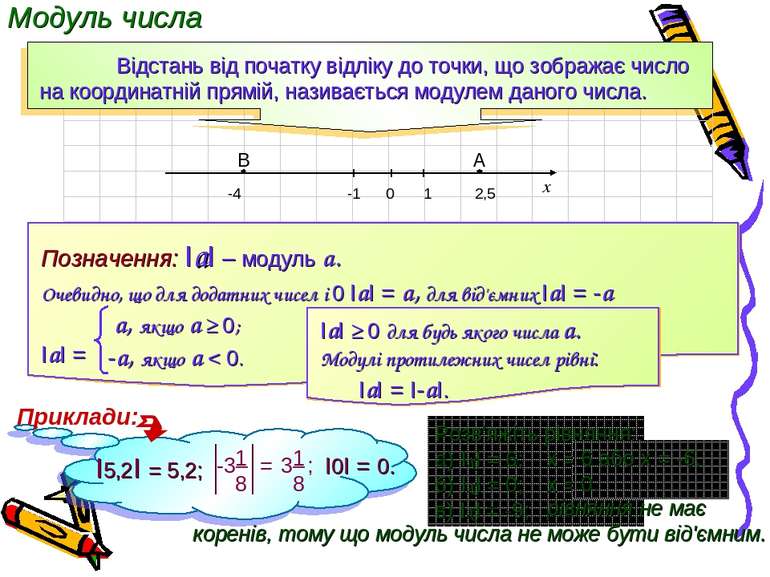
-4 А В х Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається координатною прямою. Число, що показує положення точки на координатній прямій, називається координатою точкою. Точка А розташована на прямій на відстані 2,5 одиничних відрізка праворуч від 0. Позначається: А(2,5). Точка В розташована на прямій на відстані 4 одиничних відрізка ліворуч від 0. Позначається: В(-4). Число 0 не є ні додатним, ні від'ємним. Два числа, що відрізняються одне від одного лише знаком, називаються протилежними числами. Додатні та від'ємні числа 0 1 -1 2,5

Позначення: N – множина натуральних чисел Z – множина цілих чисел Q – множина раціональних чисел R – множина дійсних чисел Дійсні числа можна додавати, віднімати, множити, підносити до степеня й ділити (ділити на числа, що відмінні від 0).

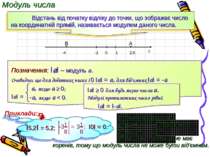
Модуль числа І5,2І = 5,2; -3– = ; 1 8 I0I = 0. Приклади: Розв'яжіть рівняння: а) IхI = 6; х = б) IхI = 0; х = в) IхI = -9; 6 або х = -6. 0. рівняння не має коренів, тому що модуль числа не може бути від'ємним.

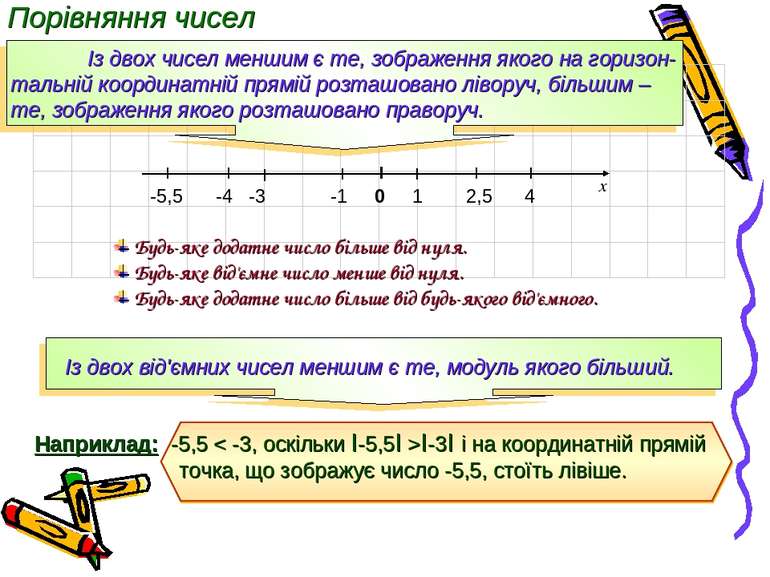
Порівняння чисел Із двох чисел меншим є те, зображення якого на горизон-тальній координатній прямій розташовано ліворуч, більшим – те, зображення якого розташовано праворуч. Будь-яке додатне число більше від нуля. Будь-яке від'ємне число менше від нуля. Будь-яке додатне число більше від будь-якого від'ємного.

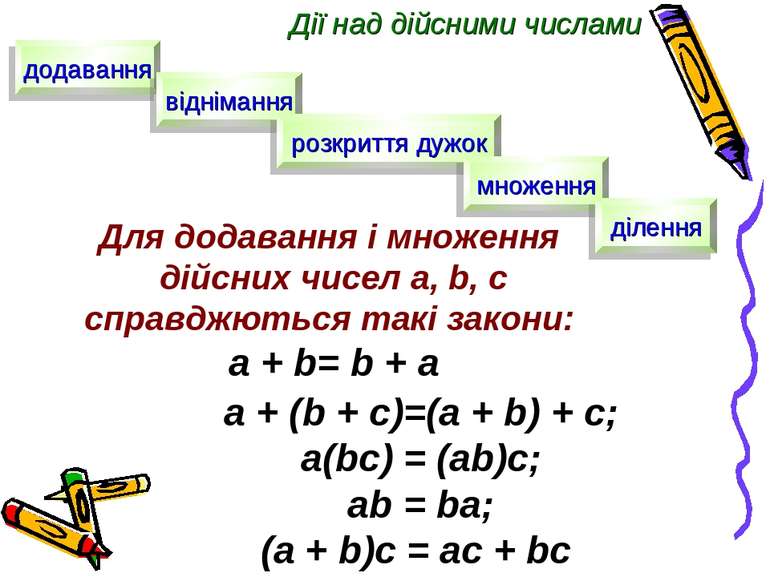
Дії над дійсними числами додавання віднімання розкриття дужок множення ділення Для додавання і множення дійсних чисел a, b, c справджються такі закони: а + b= b + a а + (b + c)=(a + b) + c; а(bc) = (ab)c; аb = ba; (a + b)c = ac + bc

Завдання 1 Розгляньте рівності. Чи правильні вони? Які закономірності ви помітили? Спробуйте продовжити записи. а) 1 + 9⋅0 = 1, б) 1 + 8⋅1 = 9, 2 + 9⋅1 = 11, 2 + 8⋅12 = 98, 3 + 9⋅12 = 111; 3 + 8⋅123 = 987.

Один сірник – одна помилка Із сірників складена неправильна рівність. Переставте у рівності по одному сірнику так, щоб отримати правильну рівність.

Відсотки Відсотком називають –– (0,01) і позначають 1%. Один відсоток від якої-небудь величини означає 0,01 цієї величини. 1 100 100% деякої величини – це сама величина.

Будь-який десятковий дріб можна записати у відсотках. Для цього його треба помножити на 100: Напр. 0,37 = 37%; 6 = 600%; 1,27 = 127%. 0,251 = 25,1%; – = 0,4 = 40% 2 5

Будь-яке число відсотків можна записати у вигляді десяткового дробу. Для цього треба число відсотків поділити на 100: Напр. 238% = 2,38; 2% = 0,02.

Щоб знайти відсотки від числа, треба це число поділити на 100 й помножити на число відсотків. Напр. 24% від 80 – це 80:100•24 = 19,2

Щоб знайти число за його відсотками, тобто якщо відомо, скільки відсотків від шуканого числа становить дане число, треба помножити дане число на 100 й поділити на число відсотків. Напр. знайдемо число, якщо 35% його становлять 14 14•100:35 = 40

Щоб знайти, скільки відсотків становить одне число від іншого, треба перше число поділити на друге, а одержаний десятковий дріб записати у вигляді відсотків (тобто помножити на 100). Напр. треба визначити, скільки відсотків становить 24 від 40. 24:40•100 = 60%

Як виникли натуральні числа? Як прочитати багатоцифрове число? Які числа називають цілими? Як позначають множину натуральних і цілих чисел? Які числа називають раціональними? Як позначають раціональні числа? Що називають модулем числа a ? Як порівнюють раціональні числа? Які дії можна виконувати у множині дійсних чисел? Запитання для закріплення матеріалу