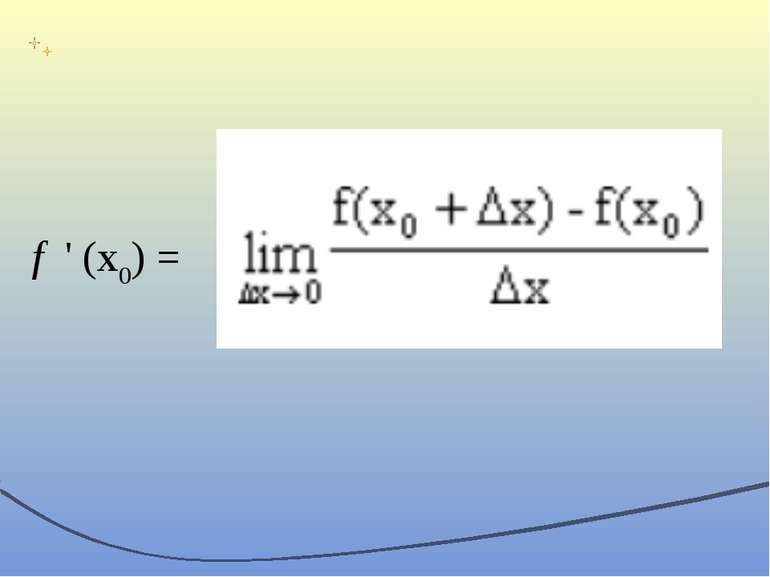
Презентація на тему:
Похідна, її використання для дослідження функцій і побудови їх графіків та розв'язування задач економічного змісту

Ткаченко Юлія Олександрівна

Мої особисті досягнення Олімпіади з географії, астрономії – III місце (2011 р.), Призер обласного конкурсу з астрономії «Людина. Космос. Духовність» - III місце (2011 р.), Міжнародного конкурсу «Колосок» з біології – II місце, Переможець конкурсу – захисту – науково-дослідницьких робіт МАН (2009 р.) з географії за темою «Демографічна ситуація в Україні» - I місце в міському етапі, IV місце в обласному.

Тема моєї роботи Похідна, її використання для дослідження функцій і побудови їх графіків та розв'язування задач економічного змісту

Актуальність роботи сучасні фахівці повинні добре володіти математичним апаратом, який має надзвичайне значення для розвитку сучасної промисловості, економіки, бізнесу, фінансової справи Фундаментом математики служить математичний аналіз. Основою математичного аналізу – взаємопов’язані за змістом розділи – диференціальне та інтегральне числення Похідна – це одне з важливих понять в математиці. І, як сказав голландський фізик Х.Гюйгенс: «Без інтегрального і диференціального числення математика, як наука, не змогла би досягнути досконалого свого розвитку».

Метою даної роботи є узагальнення та систематизація теоретичних відомостей про диференціальне числення та розгляд його застосування для розв’язання прикладних задач Розглянути застосування диференціального числення для розв’язання прикладних економічних задач Спробувати допомогти донести даний матеріал роботи до учнів і вчителів у навчальній і позакласній роботі Задачі

f ' (х0) =

З історії виникнення диференційного числення І.Ньютон Ж.Лагранж О.Коші

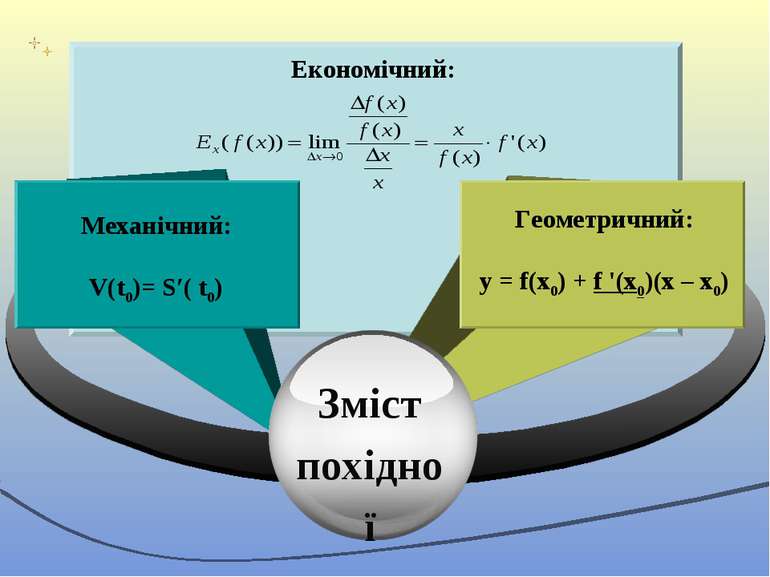
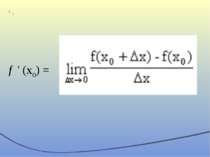
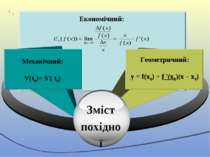
Механічний: V(t0)= S′( t0) Геометричний: y = f(х0) + f '(х0)(x – х0) Зміст похідної Економічний:

Правила диференціювання функцій Теорема 1 Теорема 3 Text in here (U V)′ = U′ V′ Теорема 2 (UV)′=U′V+UV′ (( x+5)(x-8))’= =(x+5)’(x-8)+(x-8)(x+5)’= =x-8+x+5=2x-3

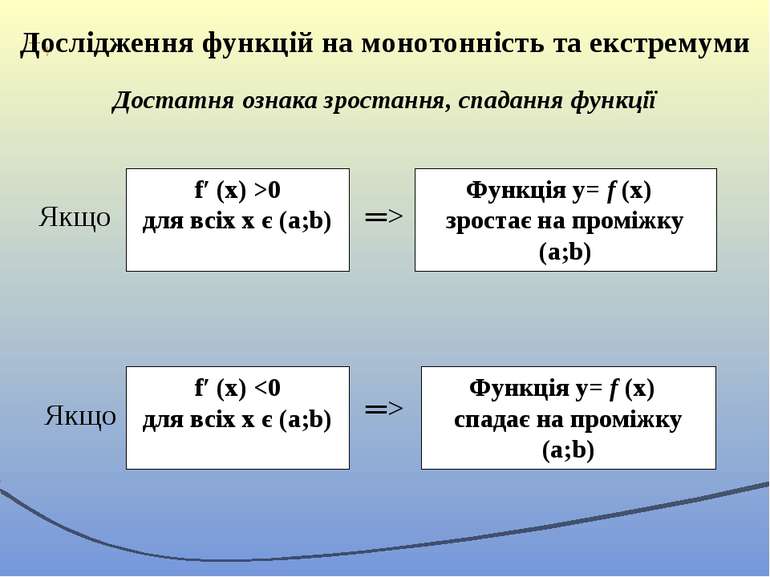
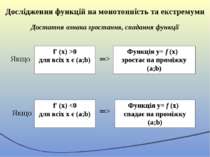
Дослідження функцій на монотонність та екстремуми Достатня ознака зростання, спадання функції Якщо f′ (x) >0 для всіх x є (a;b) ═> Функція у= f (х) зростає на проміжку (a;b) Якщо f′ (x) Функція у= f (х) спадає на проміжку (a;b)

Приклад. Знайти проміжки зростання та спадання функції Розв’язання. Функція визначена і диференційована на множені R. Знайдемо її похідну Нулями похідної є х1=1, х2= Оскільки похідна неперервна, то вона зберігає знак на інтервалах Оскільки похідна задана квадратним тричленом з додатним коефіцієнтом при х2, то вона набуває додатних значень поза коренями, тобто f’(x)>0 на інтервалах і від’ємних між коренями, тобто f’(x)

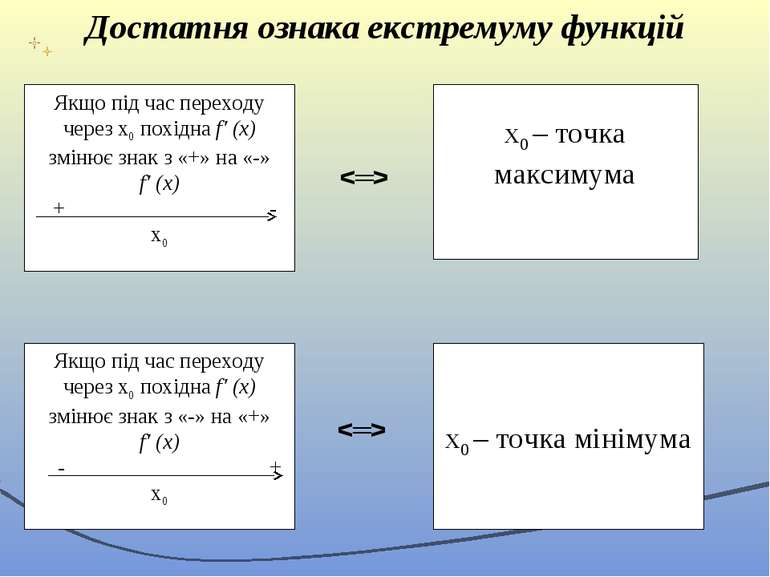
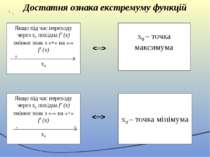
Достатня ознака екстремуму функцій Якщо під час переходу через х0 похідна f′ (x) змінює знак з «+» на «-» f′ (x) + - х0 х0 – точка максимума Якщо під час переходу через х0 похідна f′ (x) змінює знак з «-» на «+» f′ (x) - + х0 х0 – точка мінімума

Алгоритм знаходження найбільшого та найменшого значення функції 1. знаходимо похідну, 2. знаходять критичні точки в інтервалі (a;b) (точки, в яких похідна дорівнює нулю або не існує), обчислюють значення функції в цих точках; 3.знаходять значення функції на кінцях відрізка, тобто f(a),f(b) 4.серед усіх значень вибирають найбільше і найменше значення

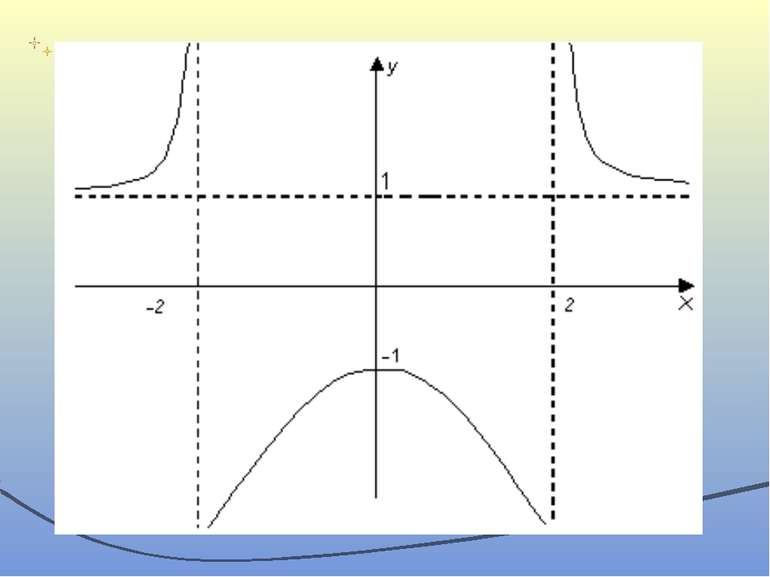
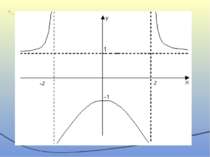
Побудувати графік функції Розв’язання X= (-∞;-2)U(-2;2)U(2;+ ∞) Функція парна. Тому її графік симетричний відносно осі ординат. Функція не є періодичною. Це випливає навіть з того, що вона невизначена лише у двох точках. Графік функції перетинає вісь ординат у точці (0;1). Нулі функції відсутні. Отже, графік функції не перетинає вісь абсцис. Дослідимо функцію на монотонність та критичні точки. Для цього знайдемо похідну х=0–критична точка.

Для хє(-∞;-2)U(-2;0) f’(x)>0 Отже, на цих проміжках функція зростає. Оскільки функція парна, то на проміжках (0;2) U(2;+∞) вона спадає. Тоді точка х=0 є точкою локального максимуму. Знайдемо його значення Дослідимо функцію на опуклість та точки перегину: На проміжках (-∞;-2)U(2;+∞) f’’(x)>0 . Отже, графік функції опуклий вниз. На проміжку (-2;2) f’’(x)

Оскільки , то пряма у=1 є горизонтальною асимптотою для графіка функції. Дослідимо поведінку функції біля точок х=2, х=-2: Отже, в точці х=2 функція має розрив другого роду, а пряма х=2 є вертикальною асимптотою. Враховуючи парність функції, робимо висновки, що пряма х=-2 також є вертикальною асимптотою.

Приклад. Знайти максимальний прибуток, якщо відома функція доходу R(Q) = 100 Q - Q2, та функція затрат C(Q) = Q3 - 37Q2 +169Q + 4000. Розв'язання. Прибуток від реалізації знайдемо за формулою П (Q) = R(Q) - C(Q) Для того, щоб прибуток від реалізації товару був максимальний, необхідно, щоб граничний дохід і граничні витрати були рівні. R′ (Q) = C′ (Q) П(Q) =100 Q- Q2-( Q3-37 Q2+169 Q+4000) П(Q) = - Q3 +36Q2 - 69Q – 4000 П'(Q) =-3Q2+72Q-69, П'(Q) =0 -3Q2+72Q-69=0 Q2 - 24Q + 23 =0 Корені цього рівняння Q1 =1, Q2=23. П(23)=-233+36·233-69·23-4000=-12167+19044-1587-4000=1290 П(1)=-13+36·12-69·1-4000=-1+36-69-4000=-4034 Перевірка показує, що максимум функції П(Q) досягається при Q2=23. Тоді Пmax=1290.

Висновки Слід погодитися з висловлюванням Ф. Енгельса: «Тільки диференціальне числення дає природознавству можливість зображувати математично не тільки стан, але і процеси: рух». Результати мого дослідження, гадаю, можуть бути використані на уроках алгебри, факультативних заняттях, позакласних заходах, які проводяться в рамках предметних тижнів. У майбутньому я планую продовжити роботу над вивченням питання про використання диференційного числення, похідної в економіці, бо мрію після закінчення 11-ого класу вступити до Харьківської інженерно-економічної академії, щоб одержати вищу освіту.