Презентація на тему:
Формування математичних компетенцій учнів

Формування математичних компетенцій учнів Олена Олексюк, методист НМЦ природничо-математичної освіти ІППО КМПУ ім. Б.Д.Грінченка

Стратегічні завдання сучасної Європейської освіти Навчити жити разом Навчити вчитися Навчити діяти Навчити жити (відповідати за власні вчинки та своє життя) (З доповіді міжнародної комісії ЮНЕСКО “Освіта. Прихований скарб”, проголошеної Ж. Делором у 1996 році)

Компетентність – ближче до “знаю, як”, ніж “знаю, що”. (З доповіді В. Хутмахера на симпозиумі, присвяченому проблемам європейської середньої освіти у 1996 р.)

Компетентність – термін, що походить від латинського слова competens (competentic), що в перекладі означає належний, здатний. Компетентність - це певна сума знань особистості, які дозволяють їй судити про що-небудь, висловлювати переконливу, авторитетну думку . (Словник іншомовних слів/За ред.І.В.Льохіна, Ф.М.Петрова, 1951 р. – 764 с.)

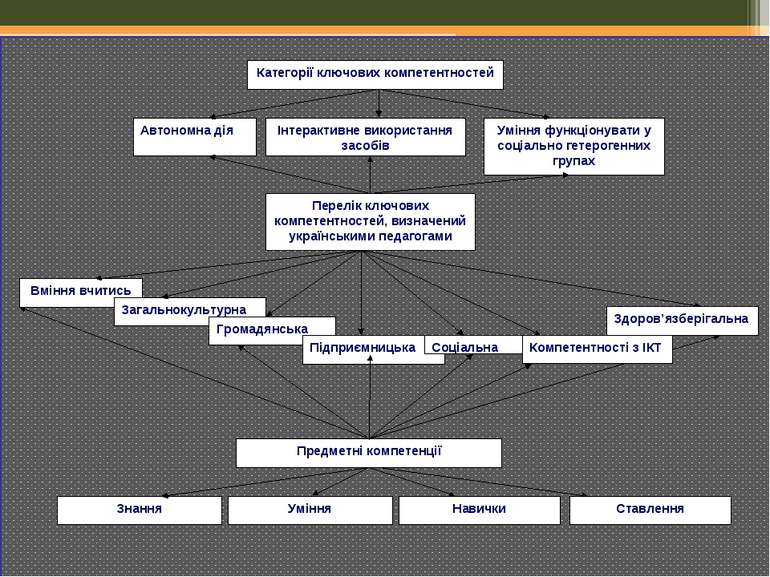
Ключові компетентності (визначені Радою Європи) Політичні та соціальні компетентності Компетентності, пов'язані з життям у мультикультурному суспільстві Компетентності, які стосуються володіння усним та письмовим спілкуванням Компетентності, пов'язані з розвитком інформаційного суспільства Щодо готовності й здатності вчитися протягом усього життя (Міжнародне дослідження “Визначення та відбір компетентностей” 1997-2003 рр.)

Аналіз експертів з Австрії, Бельгії, Данії, Німеччини, Нідерландів, Норвегії, Фінляндії, Франції, Швеції, Швейцарії, США, Нової Зеландії визначив групи компетентностей, спільні для всіх держав: компетентності щодо використання засобів ефективної взаємодії (рідної та іноземних мов, інформаційних технологій); компетентності щодо взаємодії у гетерогенних (неоднорідних) групах; компетентності щодо автономних дій у широкому соціальному контексті для реалізації особистісного потенціалу

Корисні як для кожної особистості зокрема, так і для всього суспільства в цілому; Надають можливість кожному індивідууму інтегруватись у суспільство, зберігаючи свою незалежність; Сприяють постійному вдосконаленню знань і навичок особистості відповідно до потреб часу. (З дослідження “Ключові компетентності. Концепт, що розвивається в загальній обов'язковій освіті”, організованого Європейським союзом у 2002 році)

Компетенції – еталон досвіду дій, знань, умінь, навичок, творчості, який установлює суспільство; Компетентність – рівень досягнення компетенції; Компетентісний підхід – це спрямованість освітнього процесу на формування та розвиток життєвих (ключових) і предметних компетентностей особистості, результатом якого повинна бути сформована загальна компетентність людини, що є сукупністю життєвих компетентностей, інтегрованою характеристикою особистості.

За С.Раковим, під поняттям «математична компетентність» розуміють спроможність особистості бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень.

Математичні компетентності 1. Процедурна компетентність – уміння розв’язувати типові математичні задачі. Напрями набуття: використовувати на практиці алгоритм розв’язання типових задач; уміти систематизувати типові задачі, знаходити критерії зведення задач до типових; уміти розпізнавати типову задачу або зводити її до типової; уміти використовувати різні інформаційні джерела для пошуку процедур розв’язувань типових задач (підручник, довідник, Інтернет-ресурси).

Математичні компетентності 2. Логічна компетентність – володіння дедуктивним методом доведення та спростування тверджень, необхідно: володіти і використовувати на практиці понятійний апарат дедуктивних теорій (поняття, визначення понять; висловлювання, аксіоми, теореми і їх доведення, контр приклади до теорем тощо); відтворювати дедуктивні доведення теореми та доведення правильності процедур розв’язань типових задач; здійснювати дедуктивні обґрунтування правильності розв’язання задач та шукати логічні помилки у неправильних дедуктивних міркуваннях; використовувати математичну та логічну символіку на практиці.

Математичні компетентності 3. Технологічна компетентність – володіння сучасними математичними пакетами. (пакети символьних перетворень, динамічної геометрії – Gran – 2Д(3Д), електронні таблиці (Excel); необхідно: оцінювати похибки при використанні наближених обчислень; будувати комп’ютерні моделі для предметної області задачі з метою їх евристичного, наближеного або точного розв’язання.

Математичні компетентності 4. Дослідницька компетентність – володіння методами дослідження практичних та прикладних задач математичними методами. Напрямки набуття: формулювати математичні задачі; будувати аналітичні моделі задач; висувати та перевіряти справедливість гіпотез, спираючись на відомі методи (індукція, аналогія, узагальнення), а також на власний досвід досліджень; інтерпретувати результати, отримані формальними методами; систематизувати отримані результати, досліджувати межі справедливості отриманих результатів, установлювати зв’язки з попередніми результатами, шукати аналогії в інших розділах математики.

Математичні компетентності 5. Методологічна компетентність – уміння оцінювати доцільність використання математичних методів для розв’язання практичних та прикладних задач. - аналізувати ефективність розв’язання задач математичними методами; - рефлексія власного досвіду розв’язування задач та подолання перешкод з метою постійного вдосконалення власної методології проведення досліджень.

Компонентами математичної компетентності, як і будь якої іншої, є: мотиваційний – внутрішня мотивація, інтерес; змістовний – комплекс математичних знань, умінь та навичок; дійовий – навички навчальної праці (самостійність, самооцінка, самоконтроль). Природа компетентності така, що вона може проявлятися лише в органічній єдності з цінностями людини, тобто в умовах глибокої особистої зацікавленості в даному виді діяльності.

Формування мотиваційного компонента здійснюється через: забезпечення позитивного ставлення учнів до математичної діяльності; виховання пізнавального інтересу; пізнавальну самостійність та активність. Внутрішня мотивація в багатьох учнів ще нестійка і залежить від ситуації. Тому необхідно пропонувати цікаві логікорозвивальні завдання, розв’язання ситуативних завдань, цікаві факти із життя знаменитих людей, різноманітні історичні матеріали, ігрові ситуації. Сприяють формуванню позитивної мотивації й різні форми заохочення, підтримка успіхів, емоційне спілкування. Розвитку пізнавальних інтересів та пізнавальної активності учнів математичних класів сприяє: залучення їх до самостійного пошуку й «відкриття» нових знань, розв’язання задач проблемного характеру; якщо навчання потребує напруження думки, мислення, але посильне; коли навчальний матеріал пов’язаний з раніше вивченим; завдання практичного і прикладного характеру, зокрема і старовинні; використання диференційованих дидактичних матеріалів, комп’ютерної техніки, мультимедійних засобів навчання.

Формування змістового компоненту математичної компетентності здійснюється на основі індивідуально – диференційованого підходу. Використання диференційованих різнорівневих завдань дозволяє формувати такі компетенції, як соціальні (уміння робити вибір, приймати рішення, формувати відповідальність за зроблений вибір), що,в свою чергу, стимулює пізнавальну діяльність, дозволяє формувати адекватну оцінку й самооцінку, стимулює розвиток критичного ставлення до себе. Передбачається використання різних форм організації навчальної діяльності учнів: індивідуальна; групова; фронтальна; робота в парах.

У формуванні ключових компетентностей допомагають інтерактивні технології, метод проектів, нестандартні уроки з презентацією проведених досліджень з теми. На уроках математики учні повинні розв’язувати задачі, які спонукають думати, зіставляти різні методи; сприяють розвитку мислення (творчого, критичного) і застосуванню різних способів вираження думки; інтуїції – здатності передбачати результат і знаходити шлях до розв’язання; знаходити їм практичне застосування. Навчання математики має бути спрямоване на забезпечення в учнів розвитку процедур узагальнення, порівняння, конкретизації, абстрагування, аналізу та синтезу. Саме такі задачі й краса їх розв’язання виховують хороший смак, математичну культуру.

Формуючи дійовий компонент математичної компетентності, необхідно створити для учнів оптимальні умови для поступового переходу від дій під керівництвом учителя до самостійних, даючи їм змогу самим шукати шлях розв’язання пізнавальних та практичних завдань. Встановлення ділових партнерських стосунків між учителем і учнем (діалогова взаємодія) сприяє вільному вибору, розкутості, творчій винахідливості, дослідницькій діяльності. Організація різних форм контролю навчально- пізнавальною діяльністю (фронтального, групового, індивідуального), а також само- та взаємоконтролю.

Формуванню життєвих компетентностей (саморозвитку і самоосвіти) сприяє залучення учнів до: виконання творчих завдань, написання наукових робіт, участь в інтелектуальних змаганнях (турнірах, олімпіадах, конкурсах); відвідування факультативних занять; практикування диференційованих домашніх завдань та прийомів випереджувального навчання (розширення галузі знань предмета, просування до вищого рівня засвоєння знань з теми); формування загальнонавчальних умінь.

Алгоритм формування життєвих компетентностей учнів: Участь у визначенні основних завдань уроку через спільну мотиваційно – цільову діяльність. Мотивація на актуалізацію теми, що полягає в поясненні значення матеріалу, його використання в реальному житті. Формування системи знань, отриманих у результаті активного сприймання через розв’язання проблемних ситуацій та узагальнення й аналіз фактичного матеріалу. Формування вмінь використовувати знання й особистий досвід, компетентності в життєвих ситуаціях через розв’язання ситуативних задач – участь у рольових іграх, складання проектів, виконання творчих робіт, дослідницьких завдань. Формування особистої відповідальності за рівень знань і самоосвітньої діяльності через тренінги з формування життєвих навичок – рефлексія (самопізнання, самоконтроль, саморегуляція). Моніторинг і корекція розвитку особистості через виховання і самовиховання, діагностика. Формування «Портфоліо успіху» ( замість незнання оцінюються успіхи у просуванні учня в розвитку, виконанні різних завдань).