Презентація на тему:
Застосування інтеграла у фінансових задачах

Тема: Застосування інтеграла у фінансових задачах

ПЛАН 1. Оцінка ступеня нерівномірності розподілу доходів населення 2. Розрахунок початкової суми за її кінцевим результатом 3. Максимізація прибутку за часом

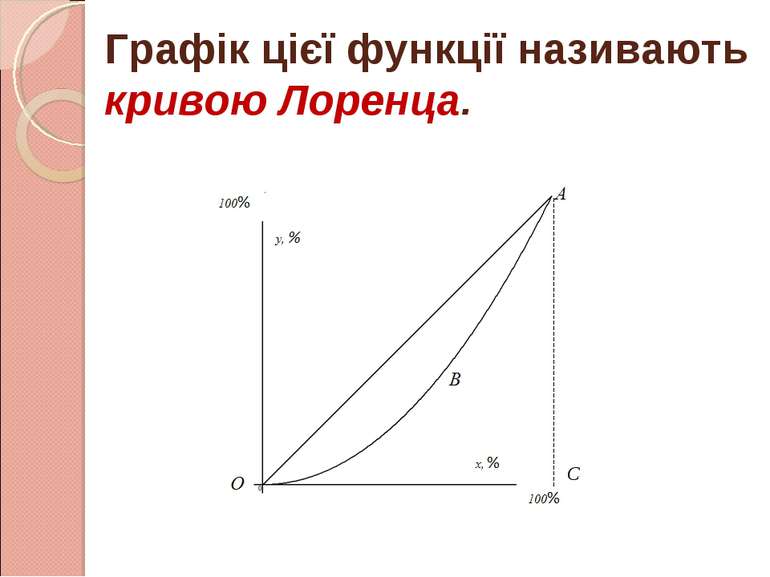
1. Оцінка ступеня нерівномірності розподілу доходів населення Розглянемо функцію у = f(x), яка характеризує нерівно- мірний розподіл доходів населення, де у – частка сукупного доходу, яку одержує частина х населення.

Графік цієї функції називають кривою Лоренца. С

Очевидно, що 0 ≤ f(x) ≤ х при х є [0; 1], і нерівномірність розподілу доходів тим вища, чим більша площа фігури ОАВ.

Тому, як міру нерівномірності використовують коефіцієнт Джині, який дорівнює відношенню площі фігури ОАВ до площі трикутника ОАС.

Дамо детальне пояснення процесу побудови кривої Лоренца. Нехай у є частина загального прибуткового податку пропорційна частині х усього населення держави.

Наприклад, якщо х = 0,5, а у =0,25, то це означає, що 50% населення сплачує 25% загального прибуткового податку. Якщо у = 0,7, коли х = 0,9, то це означає, що 90% населення сплачує 70% прибуткового податку.

У загальному випадку х та у дробові частини цілого (0 ≤ х ≤ 1;0 ≤ у ≤ 1) і у є функцією від х, тобто у = f (х).

Будемо вважати, що не має осіб, які не сплачують прибуткового податку, тобто f (0) = 0 і весь прибутковий податок сплачує 100% населення, тобто f (1) = 1. Отже, маємо криву Лоренца.

Нехай крива Лоренца: Якщо х = 0,2, то у = 0,05. Це означає, що 20% населення сплачує 5% загального податку. Коли х = 0,5, то у = 0,02656. Це означає, що 50% населення сплачує тільки 26,56% податку.

Очевидно, що 0 ≤ f(x) ≤ х при х є [0; 1], і нерівномірність розподілу доходів тим вища, чим більша площа фігури ОАВ.

Тому, як міру нерівномірності використовують коефіцієнт Джині, який дорівнює відношенню площі фігури ОАВ до площі трикутника ОАС. Коефіцієнт нерівного розподілу податку позначають L.

Площа трикутника ОАС: S∆ =0,5∙1∙1=0,5. Площу фігури, обмеженої параболою та прямою, одержимо з використанням визначеного інтеграла за формулою:

Тому, згідно з означенням, коефіцієнт Лоренца обчислюють за формулою:

Розглянемо випадок кривої Лоренца вигляду Обчислимо коефіцієнт нерівності розподілу податку.

Відмітимо, що коефіцієнт нерівномірності розподілу податку завжди задовольняє співвідношенню: 0 ≤ L≤ 1. Коли L= 0, прибутковий податок розподілено рівномірно, коли L = 1, нерівномірність розподілу податків найбільша.

Приклад. За даними досліджень розподілу доходів населення деякої країни крива Лоренца описується кривою 1 – х2 = (1 – у)2, де у частка сукупного доходу, яку одержує частина х населення. Обчислити коефіцієнт Джині.

2. Розрахунок початкової суми за її кінцевим результатом При розрахунку економічної активності капітальних вкладень зустрічаються задачі розрахунку початкової суми за її кінцевою величиною, отриманою через час t (років) при річному відсотку р. Цей процес називається дисконтуванням.

Нехай К1 – кінцева сума, отримана за t років, і К дисконтована (початкова) сума, яку в фінансовому аналізі називають також сучасною сумою.

Якщо відсотки прості, то К1 = К (1+іt), де і=0,01t – питома відсоткова ставка. Тоді

У разі складних відсотків К1 = К (1+іt)t, тому

У випадку неперервного нарахування відсотків К1 = Кеtі, і тому К = К1е-tі.

Нехай щорічний прибуток, що надходить, змінюється за часом і описується функцією f(x), та при питомій нормі відсотка, що дорівнює t, відсоток нараховується неперервно.

В цьому випадку дисконтований прибуток К за період Т обчислюється за формулою:

Приклад. Визначитидисконтований прибуток за три роки при відсотковій ставці 8%, якщо базові капіталовкладення склали 10 млрд. грош.од. і передбачається щорічне збільшення капіталовкладень на 1 млрд. грош.од.

Висновок: Це означає, що через три роки буде отримана однакова нарощена сума, як за умови щорічних капіталовкладень у розмірах від 10 до 13 млрд. гр. од., так і за умови, що одночасні первісні вкладення складали 30,5 млрд. гр. од. (при тій же відсотковій ставці та неперервному нарахуванні відсотків).

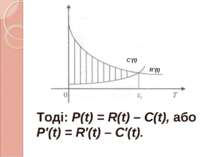
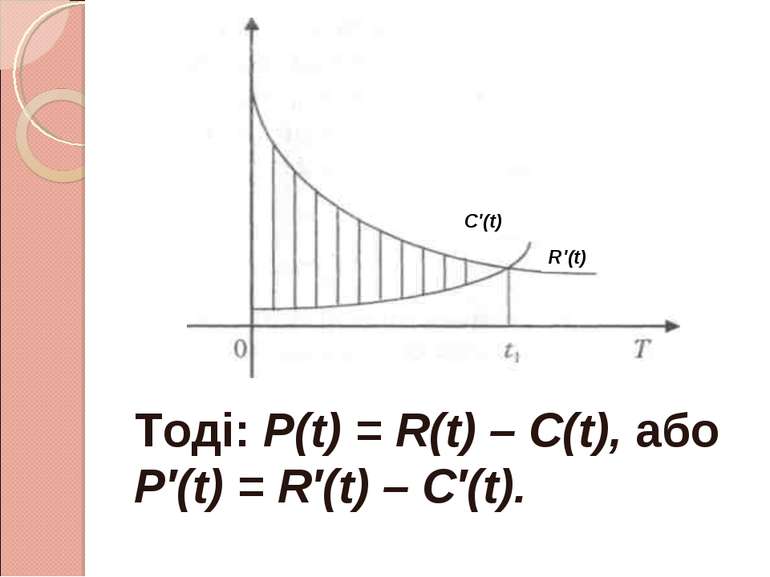
3. Максимізація прибутку за часом Нехай С(t), R(t), та Р(t) – загальні витрати, доход та прибуток, що змінюються з часом, тобто залежать від часу t.

Тоді: Р(t) = R(t) – C(t), або Р′(t) = R′(t) – C′(t). С′(t) R′(t)

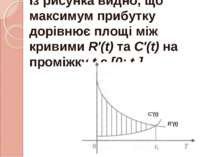
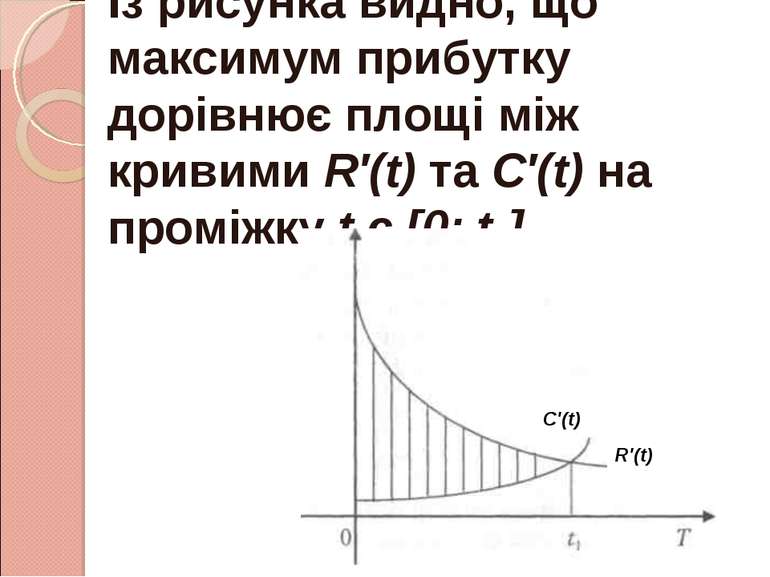
Максимум загального прибутку буде тоді, коли Р′(t) = 0, або R′(t) = C′(t). Іншими словами, існує такий час t1, коли швидкості зміни доходу на витрати рівні.

Виходячи з цього загальний прибуток за час t1 можна знайти за формулою:

Із рисунка видно, що максимум прибутку дорівнює площі між кривими R′(t) та C′(t) на проміжку t є [0; t1]. C′(t) R′(t)

Приклад. Швидкості зміни витрат та доходу його діяльності визначається формулами: С′(t)=5 + 2t2/3 та R′(t)=17 – t2/3, де С та R вимірювались млн. грн., а t – роками. Визначити, як довго підприємство було прибутковим та знайти загальний прибуток, який було одержано за цей час.

Приклад. Компанія повинна обрати одну із двох можливих стратегій розвитку: 1) вкласти 10 млн. грн. у нове обладнання і одержувати 3 млн. грн. прибутку кожного року на протязі 10 років;

2) закупити на 15 млн. грн. більш досконале обладнання, яке дозволить одержати 5 млн. грн. прибутку щорічно на протязі 7 років. Яку стратегію треба обрати компанії, якщо номінально облікова щорічна ставка 10%?