Презентація на тему:
Немає жодної сфери математики, яка коли – не будь не знайде застосування для вивчення явищ реального світу

Немає жодної сфери математики, яка коли – не будь не знайде застосування для вивчення явищ реального світу М.І.Лобачевський

Тема заняття: Тригонометричні функції числового аргументу. Співвідношення між тригонометричними функціями одного і того ж аргументу

План заняття Одиничне коло. Радіанна та градусна міра кута. Формули переходу від градусної міри до радіанної і навпаки. Означення синуса числового аргументу. Монотонність та знаки синуса на чвертях. Означення косинуса числового аргументу. Монотонність та знаки косинуса на чвертях. Означення тангенса. Вісь тангенсів. Означення котангенса. Вісь котангенсів. Таблиця значень тригонометричних функцій для деяких кутів. Співвідношення між тригонометричними функціями одного і того ж аргументу

Вавілоняни вже на початку III тисячоліття до н.е. мали календар з розподілом року на 12 місяців. Отже вони вміли визначати положення сонця і зірок на небосхилі, тобто володіли певними знаннями тригонометричного характеру. Велике значення для розвитку тригонометрії в період її зародження мали праці грецьких учених. Протягом тисячі років тригонометрія була підсобною наукою у астрономії. Складалися нові таблиці, знаходилися нові залежності між тригонометричними функціями, за допомогою яких розв’язувалися складні задачі, але тригонометрія залишалася тільки частиною астрономії, самостійної науки не існувало.

Слово “тригонометрія” складається із двох грецьких слів: “триганон” – трикутник і “метрайн” – вимірювати. У буквальному значенні “тригонометрія” означає “вимір трикутників”. Астрономія, а разом з нею і тригонометрія виникли і розвивалися в народів з розвиненою торгівлею і сільським господарством: у вавілонян, греків, індійців, китайців. Зародилася вона багато століть тому. Про це ми можемо не тільки здогадуватись. В одному з китайських рукописів, що був написаний близько 2637 року до н.е., є відомості з астрономії, де застосовуються обчислення тригонометричного характеру.

Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька подорожей інший італієць –Амеріго Віспуччі. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових тери- торій, освоєння незліченних багатств нових земель. Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані. Такі послуги могла надати тригонометрія.

Завершальний етап у розвитку тригонометрії пов'язаний з ім’ям Леонарда Ейлера. Заняття астрономією, географією і морехідними науками неможливі без застосування тригонометрії. Але до початку XVIII ст. вона була наукою неопрацьованою, часто незручною в роботі, що іноді призводило до помилок через плутанину в знаках тригонометричних функцій у різних чвертях кола. Кожна формула виводилась з креслення і всі міркування записувалися словесно. Це змусило Ейлера переглянути доведення тригонометричних формул. Він упорядкував питання про знаки тригонометричних функцій у різних чвертях, ввів однакове позначення сторін трикутника: а, в, с і протилежних кутів А, В, С. У працях Ейлера тригонометрія набула сучасного вигляду. На підставі його робіт були укладені підручники з тригонометрії, що викладають її в строгій науковій послідовності.

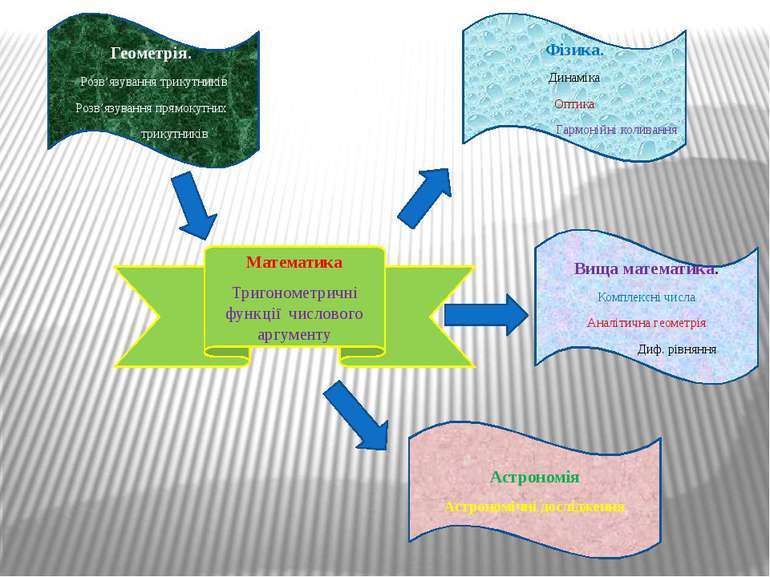
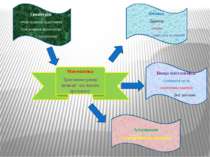
Математика Тригонометричні функції числового аргументу Геометрія. Розв’язування трикутників Розв’язування прямокутних трикутників Вища математика. Комплексні числа Аналітична геометрія Диф. рівняння Фізика. Динаміка Оптика Гармонійні коливання Астрономія Астрономічні дослідження

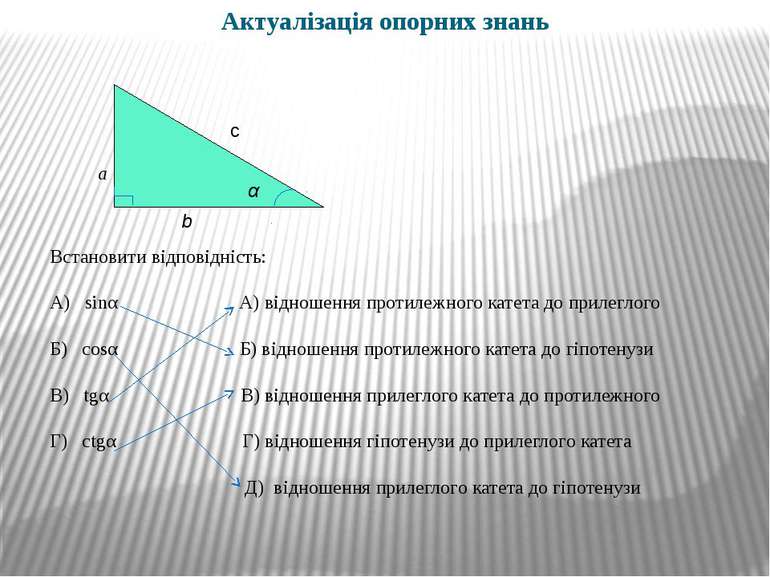
Актуалізація опорних знань Встановити відповідність: А) sinα А) відношення протилежного катета до прилеглого Б) cosα Б) відношення протилежного катета до гіпотенузи В) tgα В) відношення прилеглого катета до протилежного Г) ctgα Г) відношення гіпотенузи до прилеглого катета Д) відношення прилеглого катета до гіпотенузи c α a b

Питання №1 Одиничне коло. Радіанна та градусна міра кута. Формули переходу від градусної міри до радіанної і навпаки. (метод проектів, презентація, тренувальні вправи)

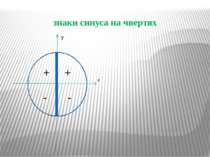
Питання №2 Означення синуса числового аргументу. Монотонність та знаки синуса на чвертях. (методи – пояснення, ілюстрації, інформаційно - комунікативний)

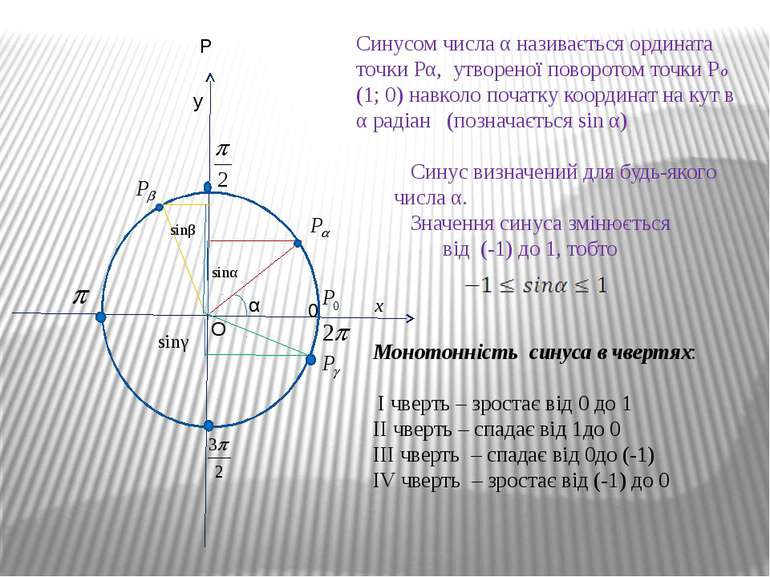
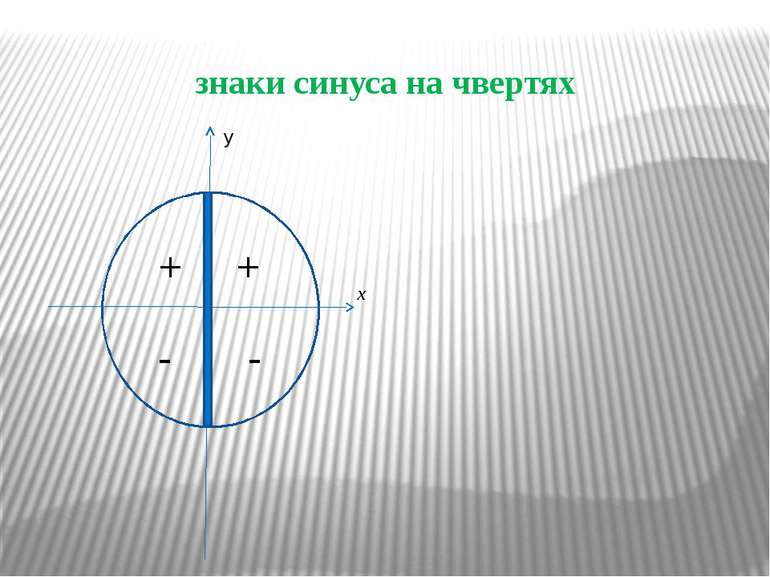
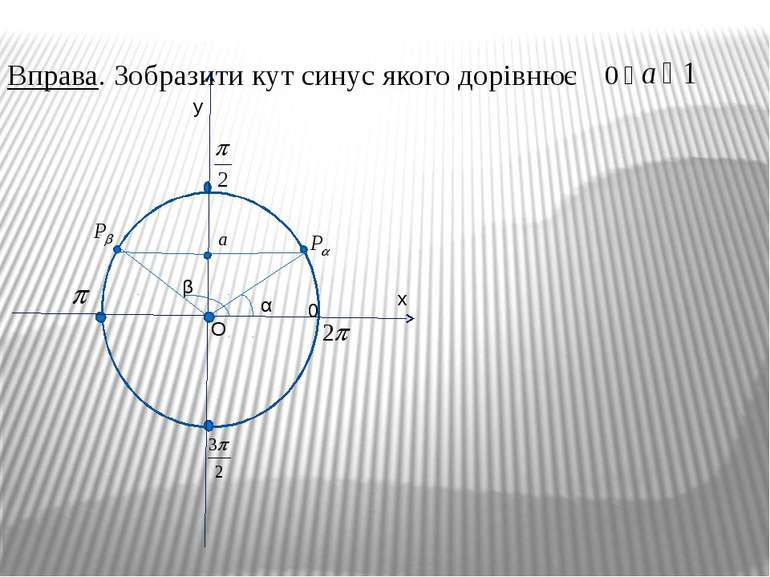
P Синусом числа α називається ордината точки Рα, утвореної поворотом точки Рo (1; 0) навколо початку координат на кут в α радіан (позначається sin α) Синус визначений для будь-якого числа α. Значення синуса змінюється від (-1) до 1, тобто Монотонність синуса в чвертях: I чверть – зростає від 0 до 1 II чверть – спадає від 1до 0 III чверть – спадає від 0до (-1) IV чверть – зростає від (-1) до 0   0 sinα sinβ sinγ y x O α

знаки синуса на чвертях + + - - y x

Вправа. Зобразити кут синус якого дорівнює 0 O α β y x a

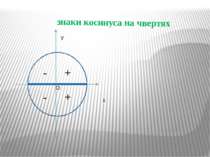
Означення косинуса числового аргументу. Монотонність та знаки косинуса на чвертях. (методи – пояснювально- ілюстративний, аналітичний) Питання №3

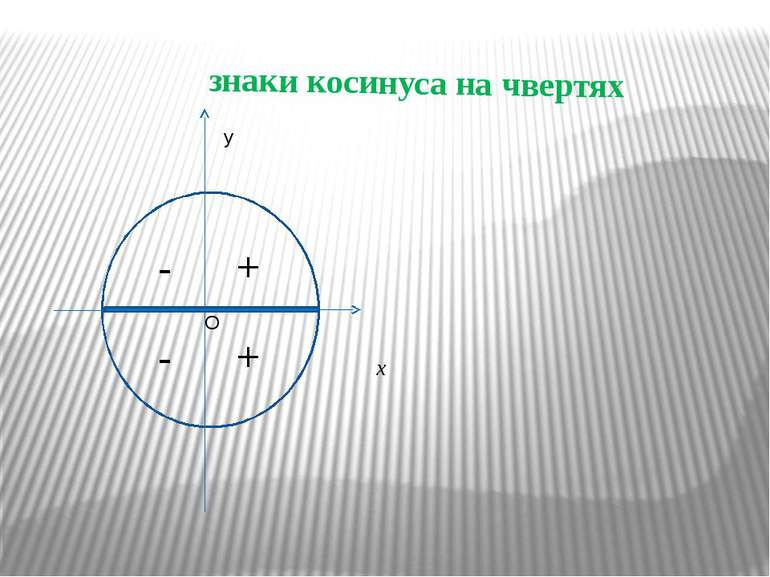
Косинусом числа α називається абсциса точки Рα, утвореної по воротом точки Рα (1; 0) навколо початку координат на кут в α радіан (позначається cos α) Косинус визначений для будь-якого числа α. Значення косинуса змінюється від (-1) до 1, тобто Монотонність косинуса в чвертях: I чверть – спадає від 1 до 0 II чверть – спадає від 0до (-1) III чверть – зростає від (-1) до 0 IV чверть – зростає від 0 до 1 cosα cosβ y x O α

знаки косинуса на чвертях x + - + - O y

Означення тангенса. Вісь тангенсів (метод – пояснювально - ілюстративний) Питання №4

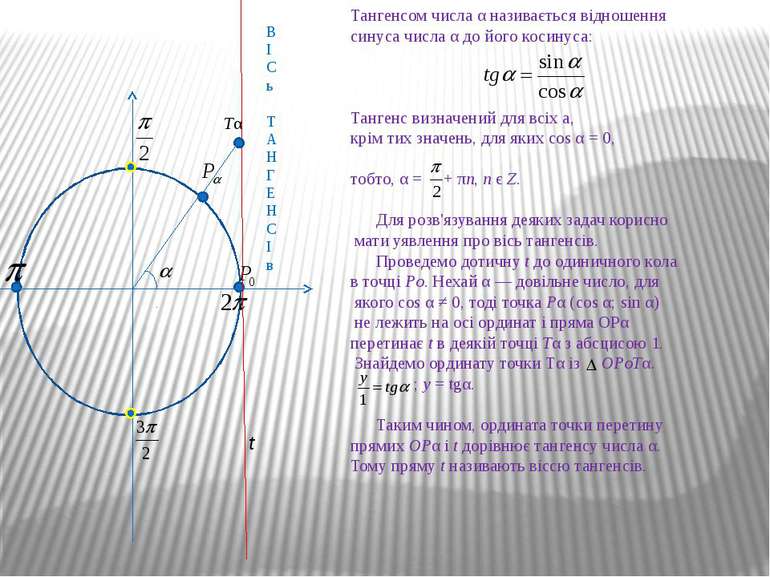
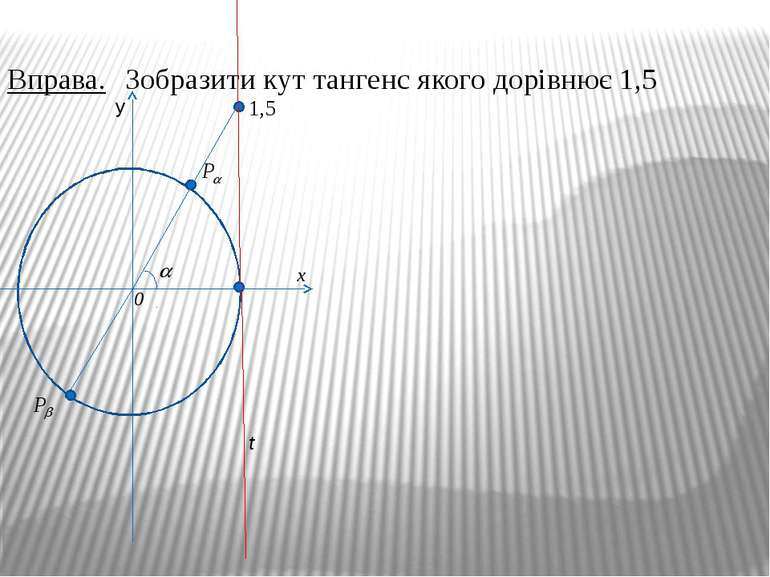
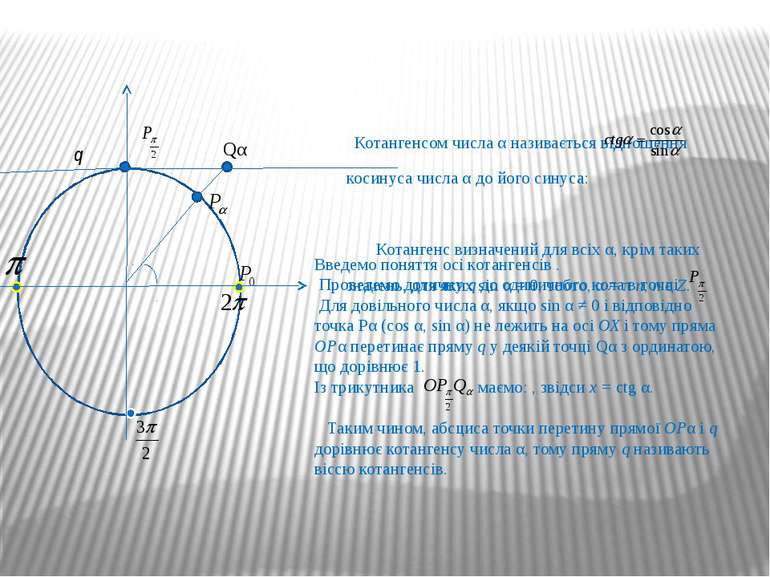
В І С ь Т А Н Г Е Н С І в Тангенсом числа α називається відношення синуса числа α до його косинуса: Тангенс визначений для всіх а, крім тих значень, для яких cos α = 0, тобто, α = + πn, n є Ζ. Для розв'язування деяких задач корисно мати уявлення про вісь тангенсів. Проведемо дотичну t до одиничного кола в точці Ρо. Нехай α — довільне число, для якого cos α ≠ 0, тоді точка Рα (cos α; sin α) не лежить на осі ординат і пряма ОРα перетинає t в деякій точці Тα з абсцисою 1. Знайдемо ординату точки Тα із ОРоТα. ; у = tgα. Таким чином, ордината точки перетину прямих ОРα і t дорівнює тангенсу числа α. Тому пряму t називають віссю тангенсів. t Тα

Вправа. Зобразити кут тангенс якого дорівнює 1,5 t 1,5 y x 0

Означення котангенса. Лінія котангенсів (методи – пояснювально – ілюстративний, навчальний тренінг) Питання №5

Котангенсом числа α називається відношення косинуса числа α до його синуса: Котангенс визначений для всіх α, крім таких значень, для яких sin α = 0, тобто, α = π n, n є Ζ. Qα q Введемо поняття осі котангенсів . Проведемо дотичну q до одиничного кола в точці Для довільного числа α, якщо sin α ≠ 0 і відповідно точка Рα (cos α, sin α) не лежить на осі ОХ і тому пряма ОРα перетинає пряму q у деякій точці Qα з ординатою, що дорівнює 1. Із трикутника маємо: , звідси х = ctg α. Таким чином, абсциса точки перетину прямої ОРα і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.

знаки тангенса і котангенса на чвертях x + - - + O y

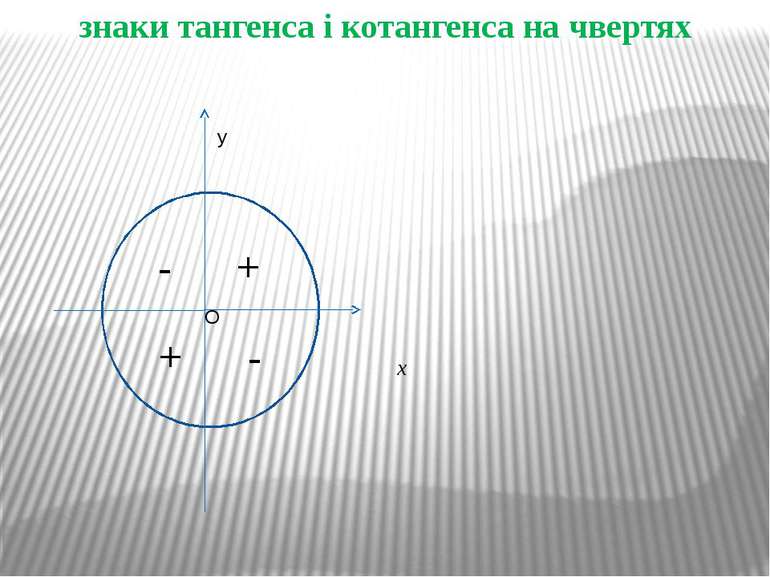
Завдання на закріплення №1. Якій чверті належить Рα, якщо: а) sin α cos α > 0; б) sin α cos α < 0; в) tg α cos α > 0; г) ctg α sin α < 0? Відповідь: а) І або III; б) II або IV; в) І або II; г) II або III. №2. Визначте знак добутку: а) tg 2 · tg 3 · ctg 3 · cos 1; б) sin 1 · cos 2 · tg 3 · ctg 4. Відповідь: а) мінус; б) плюс.

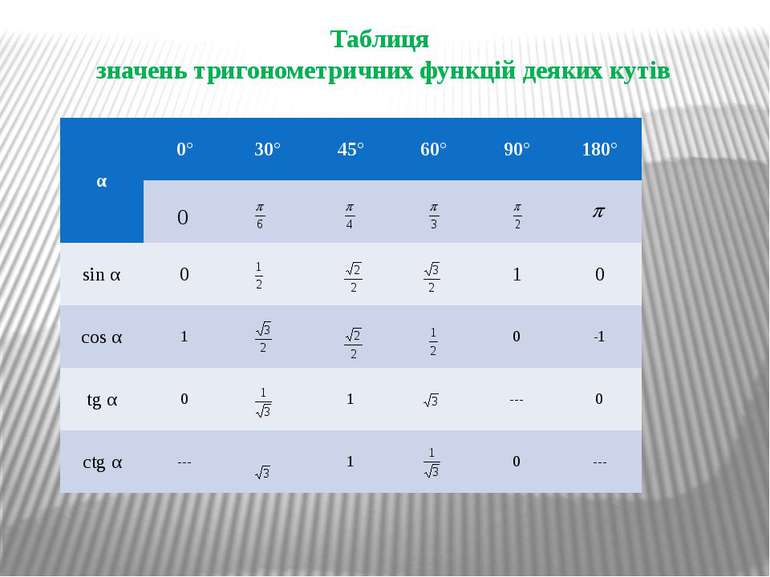
Питання №6 Таблиця значень тригонометричних функцій деяких кутів (метод – ілюстративний, тренувальні вправи)

Таблиця значень тригонометричних функцій деяких кутів α 0° 30° 45° 60° 90° 180° sin α 0 1 0 cos α 1 0 -1 tg α 0 1 --- 0 ctgα --- 1 0 ---

Завдання на закріплення №3. Обчисліть: а) 3sin + 2cos – tg ; б) 5sin +3tg – 5cos – 10ctg Відповідь: а) б)-7

Питання №7 Співвідношення між тригонометричними функціями одного і того ж аргументу (метод – доведення формул, тренувальні вправи)

1. Співвідношення між синусом і косинусом cos2 α + sin2 α = 1- основна тригонометрична тотожність (тригонометрична одиниця) 2. Співвідношення між тангенсом і котангенсом , . Звідки, перемноживши ці рівності, матимемо 3. Співвідношення між тангенсом і косинусом, котангенсом і синусом

Завдання на закріплення №4. Знайти решту функцій, якщо: Чверть Функція I II III IV sinα cosα tgα ctgα

Узагальнення та систематизація знань

сканворд “тригонометричний”

1. Наука, що в перекладі з грецької означає “Вимірювання трикутника”

1. Наука, що в перекладі з грецької означає “Вимірювання трикутника” т р и г о н о м е т р і я

2. 1/180 частина розгорнутого кута.

2. 1/180 частина розгорнутого кута. г р а д у с

3. Дуга, довжина якої дорівнює радіусу дуги.

3. Дуга, довжина якої дорівнює радіусу дуги. р а д і а н

4. Як називається коло з центром в початку координат і радіусом рівним одиниці?

4. Як називається коло з центром в початку координат і радіусом рівним одиниці? о д и н и ч н е

5. Ордината точки одиничного кола

5. Ордината точки одиничного кола с и н у с

6. Абсциса точки одиничного кола

6. Абсциса точки одиничного кола к о с и н у с

7. Відношення синуса числа до його косинуса

7. Відношення синуса числа до його косинуса т а н г е н с

8. Відношення косинуса числа до його синуса

8. Відношення косинуса числа до його синуса к о т а н г е н с

9. Дотична до одиничного кола в точці

9. Дотична до одиничного кола в точці в і с ь к о т а н г е н с і в

10. Як ще називають основну тригонометричну тотожність?

10. Як ще називають основну тригонометричну тотожність? т р и г о н о м е т р и ч н а о д и н и ц я

Підведення підсумків заняття (Рефлексія) Продовжіть речення: 1. Сьогодні я узнала… 2. Було цікаво… 3. Було важко… 4. Я зрозуміла, що… 5. Тепер я можу… 6. Я навчилась… 7. У мене вийшло… 8. Я змогла…. 9. Мене здивувало… 10. Урок дав мені для життя…

Домашнє завдання. 1. Вивчити конспект заняття. 2. М.І.Шкіль. Алгебра і початки аналізу. Розділ1, §§2-4 3. Заповнити картки із значеннями тригонометричних функцій.

Бажаю всім успіхів!