Презентація на тему:
Інтеграл

Інтеграл Воробйов Леонід Альбертович, учитель математики гімназії № 15 Радянського району, м. Мінськ

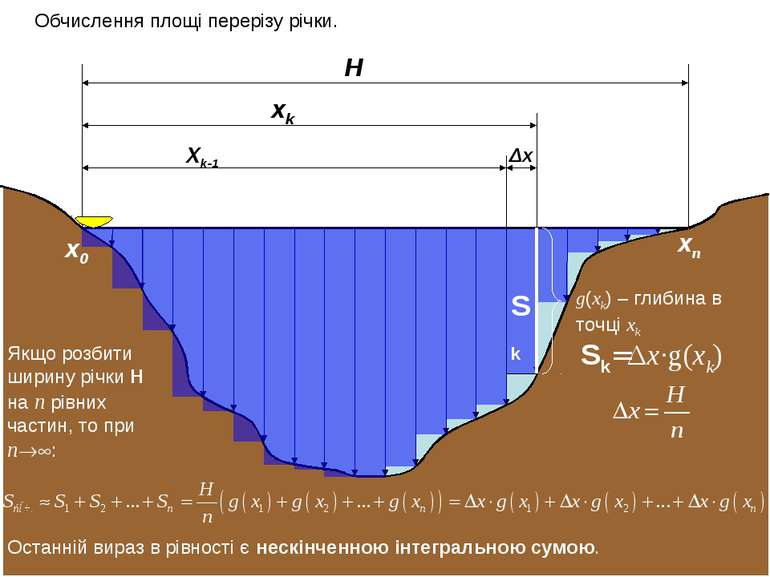
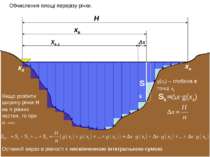
H xk Xk-1 Обчислення площі перерізу річки. Δх Sk g(xk) – глибина в точці xk Якщо розбити ширину річки H на n рівних частин, то при n : Sk=Δx∙g(xk) x0 xn Останній вираз в рівності є нескінченною інтегральною сумою.

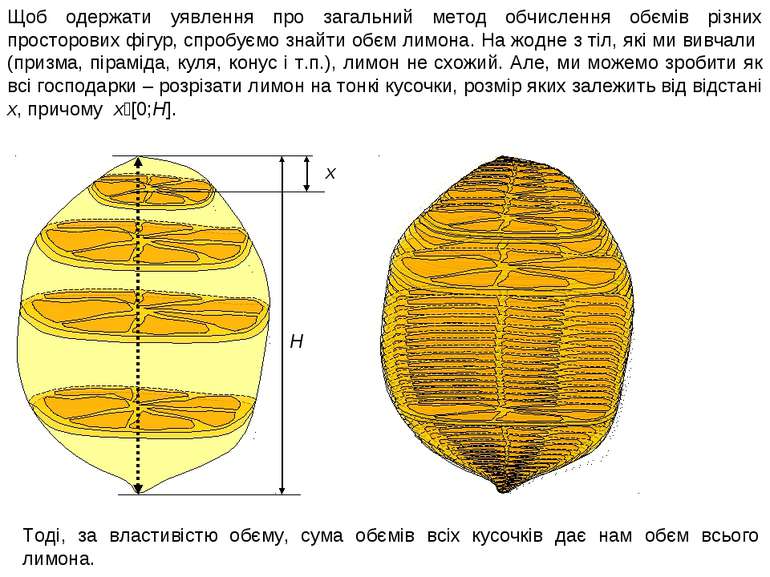
Щоб одержати уявлення про загальний метод обчислення обємів різних просторових фігур, спробуємо знайти обєм лимона. На жодне з тіл, які ми вивчали (призма, піраміда, куля, конус і т.п.), лимон не схожий. Але, ми можемо зробити як всі господарки – розрізати лимон на тонкі кусочки, розмір яких залежить від відстані x, причому x [0;H]. H x Тоді, за властивістю обєму, сума обємів всіх кусочків дає нам обєм всього лимона.

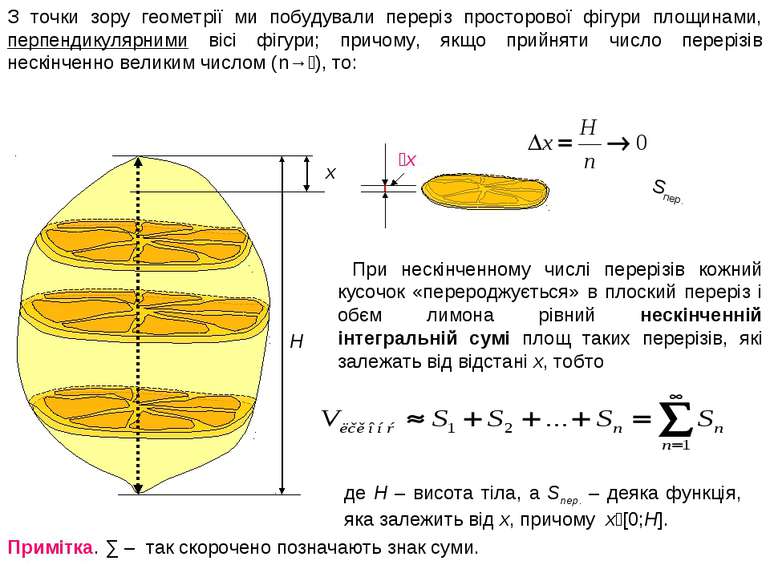
H x x З точки зору геометрії ми побудували переріз просторової фігури площинами, перпендикулярними вісі фігури; причому, якщо прийняти число перерізів нескінченно великим числом (n→ ), то: При нескінченному числі перерізів кожний кусочок «перероджується» в плоский переріз і обєм лимона рівний нескінченній інтегральній сумі площ таких перерізів, які залежать від відстані x, тобто де H – висота тіла, а Sпер. – деяка функція, яка залежить від x, причому x [0;H]. Sпер. Примітка. ∑ – так скорочено позначають знак суми.

x H x [0;H] 0 x Використовуючи поняття нескінченної інтегральної суми самостійно поясніть даний приклад і виведення кінцевої формули обєму прямокутного паралелепіпеда. Обєм прямокутного паралепіпеда рівний нескінченній інтегральній сумі площ перерізів (рівних площі основи) на проміжку [0; H] .

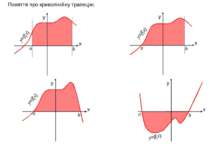
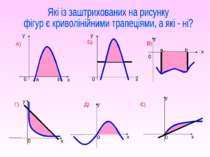
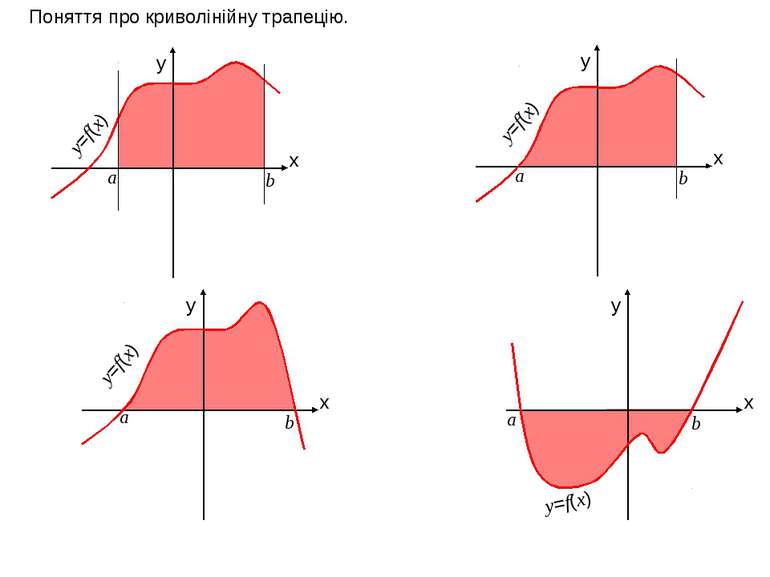
x y x y x y x y Поняття про криволінійну трапецію. а b y=f(x) а b а b а b y=f(x) y=f(x) y=f(x)

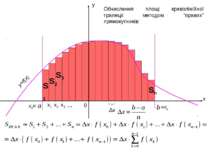
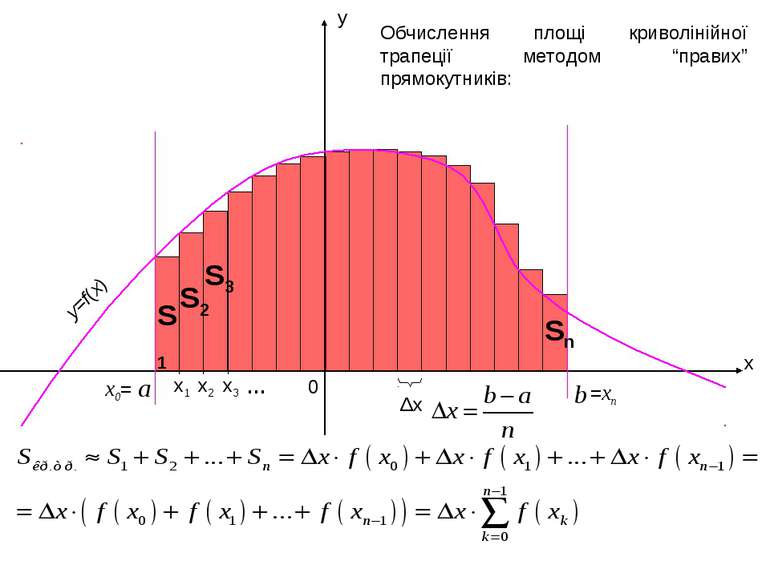
x1 x y a b 0 x2 x0= x3 =xn y=f(x) … Δx Обчислення площі криволінійної трапеції методом “правих” прямокутників: S1 S2 S3 Sn

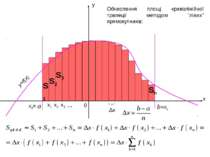
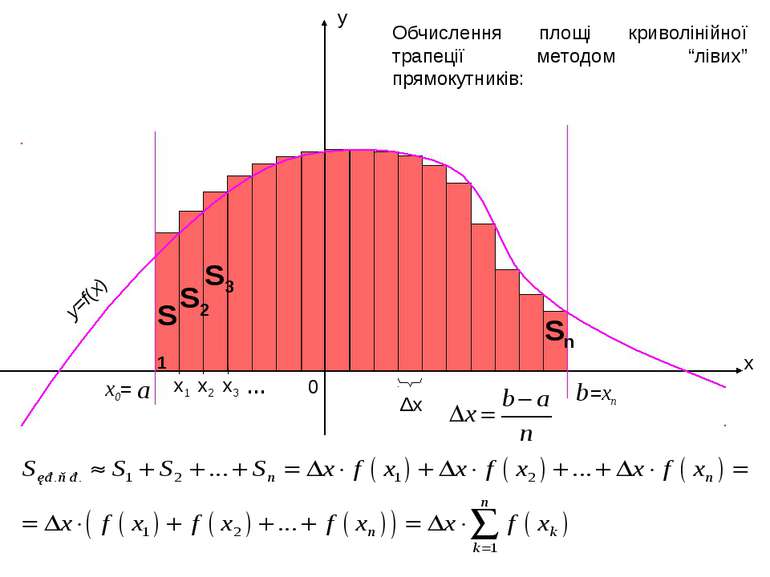
x y a b 0 Δx Обчислення площі криволінійної трапеції методом “лівих” прямокутників: x1 x3 x2 y=f(x) x0= =xn … S1 S2 S3 Sn

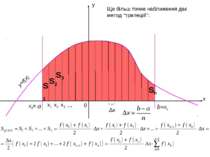
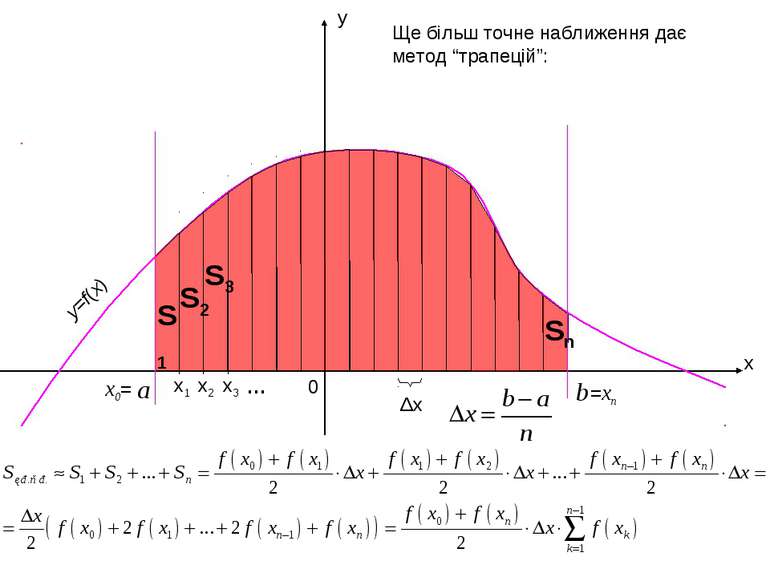
x y 0 Δx Ще більш точне наближення дає метод “трапецій”: y=f(x) a x1 x3 x2 x0= … b =xn S1 S2 S3 Sn

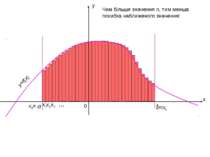
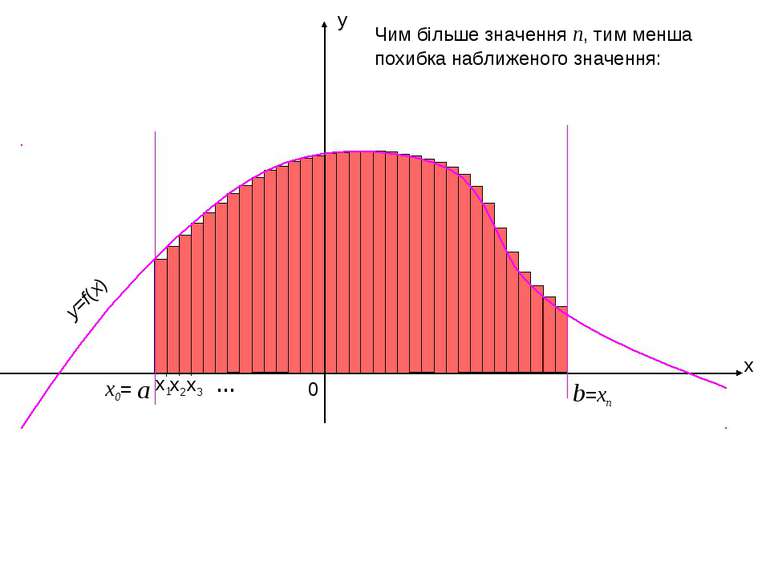
x y b 0 x2 x1 x3 =xn … Чим більше значення n, тим менша похибка наближеного значення: y=f(x) a x0=

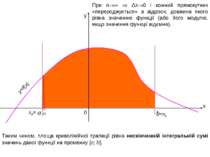
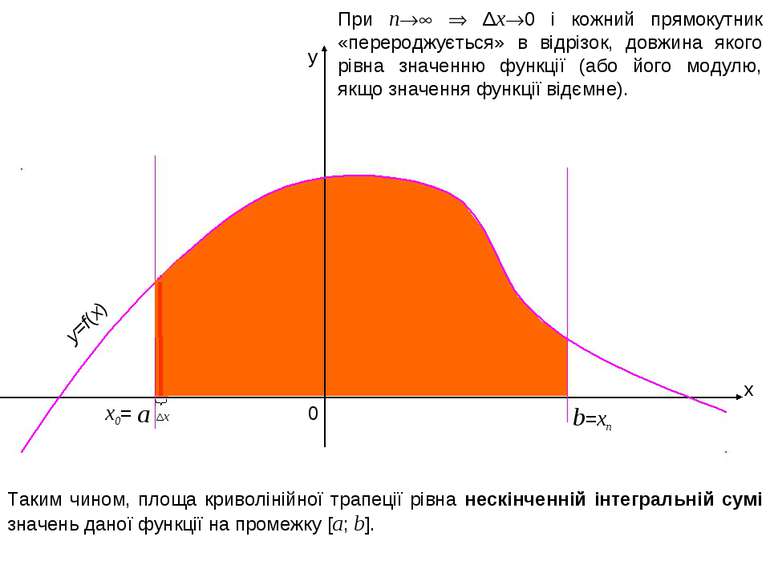
x y b 0 =xn При n Δx 0 і кожний прямокутник «перероджується» в відрізок, довжина якого рівна значенню функції (або його модулю, якщо значення функції відємне). y=f(x) a x0= Таким чином, площа криволінійної трапеції рівна нескінченній інтегральній сумі значень даної функції на промежку [a; b]. Δx

В наведеному вище прикладі ми знаходили площу криволінійної трапеції з допомогою поняття нескінченної інтегральної суми значень даної функції f(x) на проміжку [a; b]. В математиці прийнятий більш короткий запис цього поняття – інтеграл (∫), тобто Примітка. Зверніть увагу, що знак інтеграла нагадує стилізовану букву S, що природньо з геометричного змісту цього поняття. Читають: інтеграл від a до b еф від ікс де ікс. Число a називають нижньою границею інтегрування, b – верхньою границею інтегрування, f(x) – підінтегральна функція, x – змінна інтегрування. Користуючись поняттям границі (lim) можна дати слідуюче означення інтеграла: , де xn [a; b].

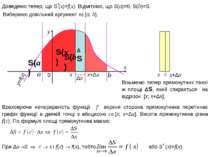
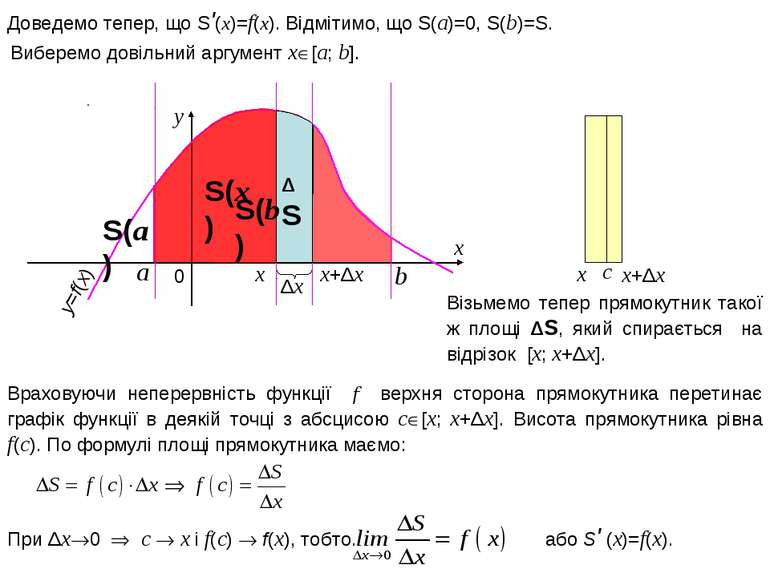
x+Δx x y 0 x y=f(x) Доведемо тепер, що S'(x)=f(x). Відмітимо, що S(a)=0, S(b)=S. ΔS Δx b a x+Δx x Візьмемо тепер прямокутник такої ж площі ΔS, який спирається на відрізок [x; x+Δx]. c Враховуючи неперервність функції f верхня сторона прямокутника перетинає графік функції в деякій точці з абсцисою c [x; x+Δx]. Висота прямокутника рівна f(c). По формулі площі прямокутника маємо: S(x) Виберемо довільний аргумент x [a; b]. S(a) S(b)

Ви вже знайомі поняттям первісної функції. Доведене нами твердження S'(x)=f(x) в силу основної властивості первісних для всіх x [a;b] означає, що: S(x)=F(x)+C, де С – деяка постійна, а F – одна з первісних для функції f(x). Для знаходження С підставимо x=a: F(a)+C=S(a)=0 F(a)=–C. Значить, S(x)=F(x) –F(a). Поскільки площа криволінійної трапеції рівна S(b)=S, підставляючи x=b, одержимо: S = S(b) = F(b) – F(a)=