Презентація на тему:
Інтеграли

ЗАСТОСУВАННЯ ІНТЕГРАЛІВ

Історія розвитку понять інтеграла й інтегрального обчислення Історія розвитку понять інтеграла й інтегрального обчислення пов’язана з потребою в обчисленні площ фігур, а також поверхонь і об’ємів довільних тіл. Передісторія інтегрального обчислення сягає глибокої давнини: ідеї інтегрального обчислення можна знайти в роботах давньогрецьких учених Евдокса Кнідського (бл.408-355 до н.е.) і Архімеда (бл.287-212 до н.е.).

Поняття інтегралу з'явилося в результаті практичної діяльності людини, використовується сьогодні в самих різних сферах науково-практичної діяльності людини, а саме: фізиці, хімії, біології, механіці, економіці, філології і т.д. Тому на уроці ми будемо розв'язувати задачі прикладного характеру, що допоможе зрозуміти місце і роль математики в сучасному світі. Ми з вами познайомилися з другим поняттям математичного аналізу без якого не збудувати сучасного будинка, космічного корабля, субмарини.

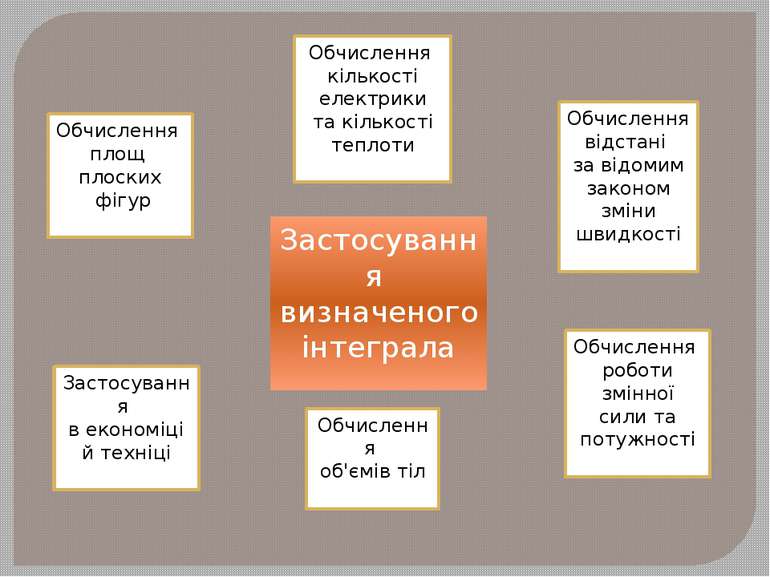
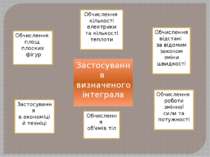
Застосування визначеного інтеграла Обчислення площ плоских фігур Застосування в економіці й техніці Обчислення об'ємів тіл Обчислення відстані за відомим законом зміни швидкості Обчислення роботи змінної сили та потужності Обчислення кількості електрики та кількості теплоти

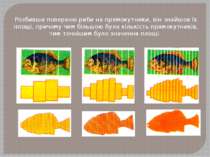
Інтеграл виник з практичної потреби знаходити площі неплоских фігур. Найбільший внесок у вивченні інтегрального числення вніс Архімед. Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.

Розбивши поверхню риби на прямокутники, він знайшов їх площі, причому чим більшою була кількість прямокутників, тим точнішим було значення площі.

Інтеграл широко застосовують під час розв'язування фізико-технічних задач різного характеру, а також задач економічного змісту.   Приклад 1 Експериментально встановлено, що продуктивність праці робітника наближено виражається формулою f(t)= -0.0033t2 - 0.089t + 20.96, де t — робочий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі — 62. Розв'язання. Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці. Тому . Протягом кварталу обсяг випуску продукції становитиме: =62(-0.001∙512 -2.848 + 167.68) = 62∙164.27≈  10185 (од.).

 Приклад 2 Експериментальне встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається формулою Q = 18 - 0,3v +0,003v2, де 30 ≤ v ≤110. Визначити середню витрату бензину, якщо швидкість руху 50 - 60 км/год. Розв'язання. Середня витрата бензину становить = 1/10(18∙60-0.3∙1800+0.003∙72000-18∙50-0.3∙1250-0.003∙41667) = = 1/10(1080-540 + 216-900 + 375- 125) = 10,6 (л). Отже, автомобіль на 100 км шляху, рухаючись зі швидкістю 50 - 60 км/год, витрачає в середньому 10,6 л бензину.

Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4м., що має квадратний переріз зі стороною 2м. Густина води ρ=103кг/м3. Розв'язання: Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м2, визначається вагою шару води, що знаходиться вище від цього перерізу. Отже