Презентація на тему:
Методи і моделі інтегрального числення

Тема: Економічні застосування інтегрального числення РОЗДІЛ ІІІ. МЕТОДИ І МОДЕЛІ ІНТЕГРАЛЬНОГО ЧИСЛЕННЯ

ПЛАН 1. Застосування в динамічних процесах 2. Обчислення середніх значень економічних функцій 3. Визначення приросту капіталу за відомими інвестиціями 4. Оцінка ступеня нерівномірності розподілу доходів населення

1. Застосування в динамічних процесах Економічний зміст визначеного інтеграла полягає у тому, що він чисельно дорівнює обсягу виробленої продукції підприємством чи фірмою з продуктивністю праці f(x) за інтервал часу [0; Т], тобто

Приклад. Продуктивність праці виробничої бригади представлено функцією f(x) = 8t – t2, що виражає обсяг виробленої продукції за інтервал часу [0; Т]. Робітники працюють 8 год, тобто t є [0; 8]. Обчислити обсяг виробленої продукції: - за восьмигодинний робочий день; - за інтервал часу [2; 6]; - порівняти ці обсяги у відсотковому відношенні.

Розглянемо виробничу функцію Кобба-Дугласа, яка враховує технічний прогрес і має вигляд у=АКαLβеλt де К – обсяг основного капіталу; L – обсяг трудових ресурсів; λ – інтенсивність розвитку виробництва, пов’язаного з технічним прогресом.

Тоді згідно з економічним змістом виробничої функції Кобба-Дугласа можна показати, що обсяг виробленої за t років продукції визначається за формулою

Приклад. Знайти обсяг продукції, виробленої фірмою за два роки, якщо виробнича функція Кобба-Дугласа має вигляд

2. Обчислення середніх значень економічних функцій Розглянемо наступні функції: С = С(t), R = R (t), Р = Р(t) – відповідно змінні витрати, доход і прибуток підприємства.

Тоді їх середні значення за час від t0 до t1 обчислюють за формулами:

Приклад. Знайти середній доход за 10 місяців поточного року, якщо задано функцію доходу фірми R(t) = 3t2 + 2t – 1, де t – час.

У попередньому розділі розглядалися різні граничні функції: граничний доход, граничні витрати, граничний прибуток.

Відомо, що граничні функції можна отримати з відповідних економічних функцій диференціюванням. Інтегрування дає змогу розв’язати обернену задачу: знайти дану економічну функцію за відомою граничною функцією.

Нехай С'(х)і R'(х), Р'(х) – відповідно функції граничних витрат, доходу та прибутку підприємства.

Тоді при реалізації х одиниць товару зміни витрат, доходу й прибутку зі збільшенням реалізації виробленої продукції від а до b одиниць обчислюють за формулами

Якщо витрати на виготовлення одиниці продукції зростають за законом f(x), то фактичне зв’язування обігових коштів при цьому обчислюють за формулою:

Умовне зв’язування обігових коштів (якщо всі витрати виплатити в перший день) Сумов = t С де t – тривалість циклу виробництва, а С – загальні витрати.

Коефіцієнт готовності одиниці продукції обчислюють за формулою:

Приклад. Задано граничний прибуток фірми Р'(х) = 23,5 – 0,01х. Визначити зростання прибутку, якщо реалізація продукції збільшується з 1000 до 1500 одиниць.

Приклад. Задано граничний доход фірми R'(х) = 15 - 0,01х. Знайти функцію доходу й визначити співвідношення між ціною одиниці продукції та обсягом проданої продукції.

Приклад. Нехай гранична ціна проданої фірмою продукції описується функцією Р'(х) = х + 100, де х – обсяг проданої продукції. Визначити загальну функцію ціни проданої продукції, якщо ціна 100 одиниць дорівнює 40000 грн.

3. Визначення приросту капіталу за відомими інвестиціями Розглянемо задачу визначення капіталу (основних фондів) за відомими чистими інвести- ціями (капіталовкладеннями).

Чисті інвестиції – це загальні інвестиції, які надходять в економіку за певний інтервал часу, із відрахуванням інвестицій на відшкодування основних фондів. Таким чином, за одиницю часу капітал збільшується на обсяг чистих інвестицій.

Припустимо, що капітал К= К(t) збільшується за одиницю часу t на обсяг чистих інвестицій І = І(t). Тоді чисті інвестиції – це похідна капіталу за часом t, тобто І(t) = К′(t).

В економічних дослідженнях доводиться знаходити приріст К= К(t) є первісною для функції капіталу за інтервал часу від t1 до t2, тобто ∆К= К(t2) – К(t1).

Оскільки К= К(t) є первісною для функції І = І(t), то, використовуючи формулу, яка пов’язує первісну з визначеним інтегралом, можна записати:

Приклад. За даними чистими інвестиціями І(t) = 50 000t капіталу з першого по третій рік і визначити, за скільки років приріст капіталу становитиме 25 000 000 умов. грош. од.

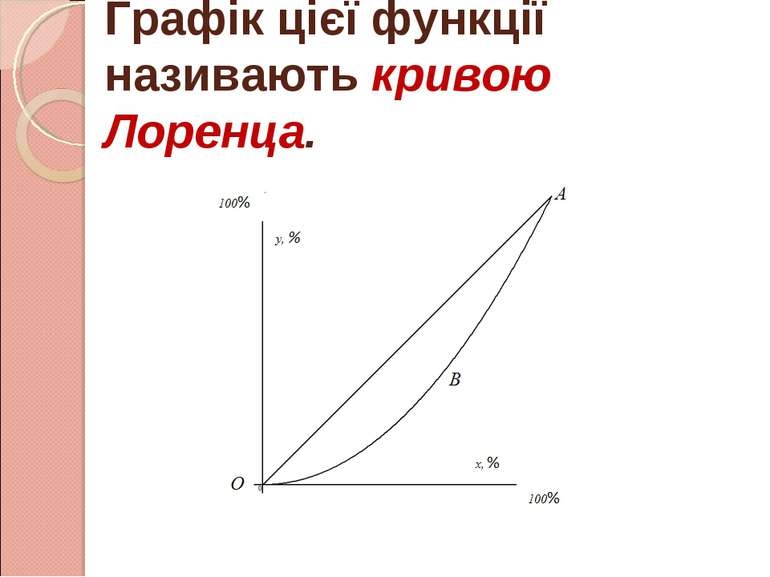
4. Оцінка ступеня нерівномірності розподілу доходів населення Розглянемо функцію у = f(x), яка характеризує нерівно- мірний розподіл доходів населення, де у – частка сукупного доходу, яку одержує частина х населення.

Графік цієї функції називають кривою Лоренца.

Очевидно, що 0 ≤ f(x) ≤ х при х є [0; 1], і нерівномірність розподілу доходів тим вища, чим більша площа фігури ОАВ.

Тому, як міру нерівномірності використовують коефіцієнт Джині k, який дорівнює відношенню площі фігури ОАВ до площі трикутника ОАС.

Приклад. За даними досліджень розподілу доходів населення деякої країни крива Лоренца описується кривою 1 – х2 = (1 – у)2, де у частка сукупного доходу, яку одержує частина х населення. Обчислити коефіцієнт Джині.