Презентація на тему:
Інтеграл

Інтеграл та його застосування Підготувала студентка 1-го курсу хорового відділу Бондар Олена 2015 рік

1. Поняття криволінійної трапеції. 2. Площа криволінійної трапеції. Формула Ньютона-Лейбніца. 3. Визначений інтеграл. 4. Застосування визначеного інтеграла до обчислення: а) площі криволінійної трапеції; б) площі фігури, обмеженої лініями; в) об'ємів многогранників (піраміди), об'ємів тіл обертання; г) об'ємів тіла, утвореного обертанням криволі- нійної трапеції; ґ) шляху за відомим законом зміни швидкості. Зміст

КРИВОЛІНІЙНА ТРАПЕЦІЯ Розглянемо функцію , яка є неперервною на відрізку і набуває на цьому проміжку невід'ємних значень. Означення: Фігуру, обмежену графіком функції і прямими називають криволінійною трапецією.

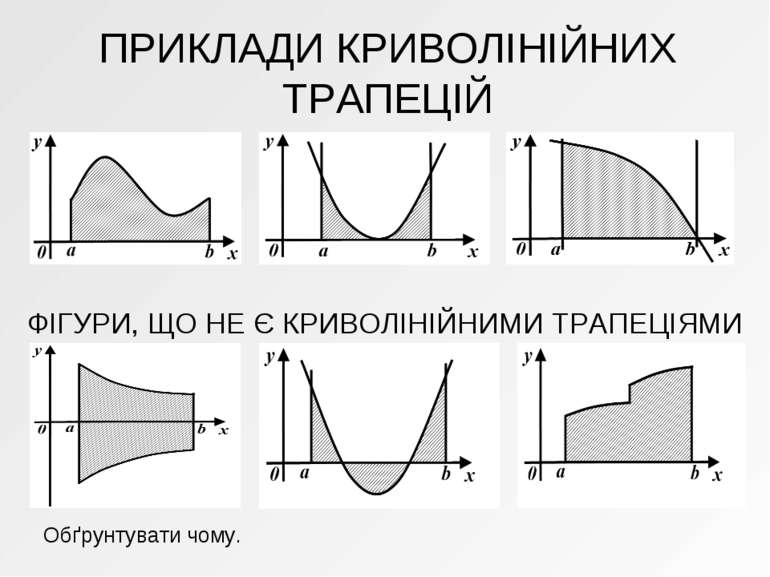
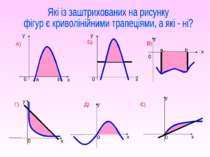
ПРИКЛАДИ КРИВОЛІНІЙНИХ ТРАПЕЦІЙ ФІГУРИ, ЩО НЕ Є КРИВОЛІНІЙНИМИ ТРАПЕЦІЯМИ Обґрунтувати чому.

ПЛОЩА КРИВОЛІНІЙНОЇ ТРАПЕЦІЇ S – площа криволінійної трапеції; F (x) – будь-яка первісна функції f(x) на відрізку [a; b]. Площу S криволінійної трапеції, обмеженої графіком функції y=f(x) і прямими y=0, x=a i x=b (a

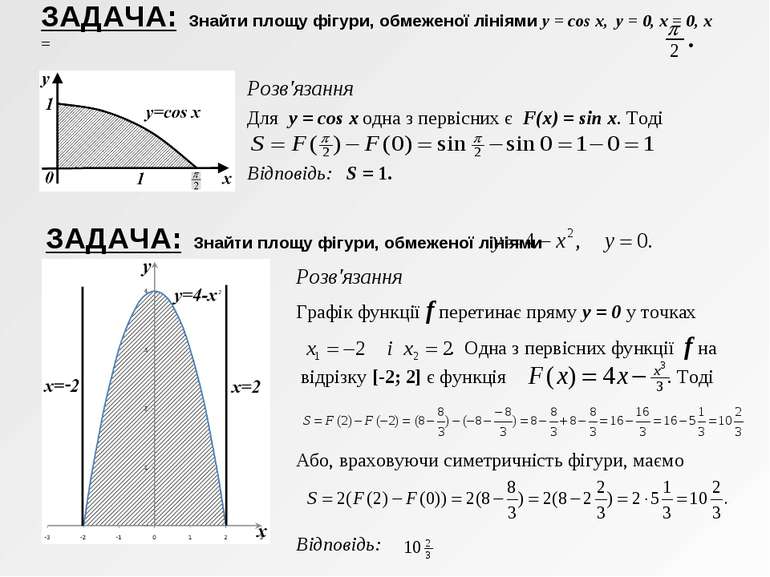
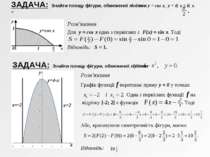
ЗАДАЧА: Знайти площу фігури, обмеженої лініями y = cos x, y = 0, x = 0, x = Розв'язання Для y = cos x одна з первісних є F(x) = sin x. Тоді Відповідь: S = 1. ЗАДАЧА: Знайти площу фігури, обмеженої лініями Розв'язання Графік функції f перетинає пряму y = 0 у точках . Одна з первісних функції f на відрізку [-2; 2] є функція . Тоді Або, враховуючи симетричність фігури, маємо Відповідь:

ВИЗНАЧЕНИЙ ІНТЕГРАЛ Означення. Нехай F – первісна функції f на проміжку I, числа a і b належать проміжку I, де a

ІСТОРИЧНА ДОВІДКА “Розумом він перевершив рід людський ” – ці слова написані нащадками про видатного англійського науковця, фізика і математика Ісаака Ньютона. Поряд з Ісааком Ньютоном стоїть ім'я німецького вченого Готфріда Лейбніца, який залишив після себе наукові праці у філософії, математиці, юриспруденції, логіці, дипломатії, політології. Ісаак Ньютон і Готфрід Лейбніц завершили теорію диференціального та інтегрального числення, що дало можливість швидко і просто розв'язувати задачі, які раніше вважалися неприступними. Завдяки зручній загальній теорії можна швидко будувати дотичні до найскладніших кривих, знаходити найбільші та найменші значення функції, обчислювати площі різноманітних фігур, об'єми просторових тіл, розв'язувати різні фізичні задачі.

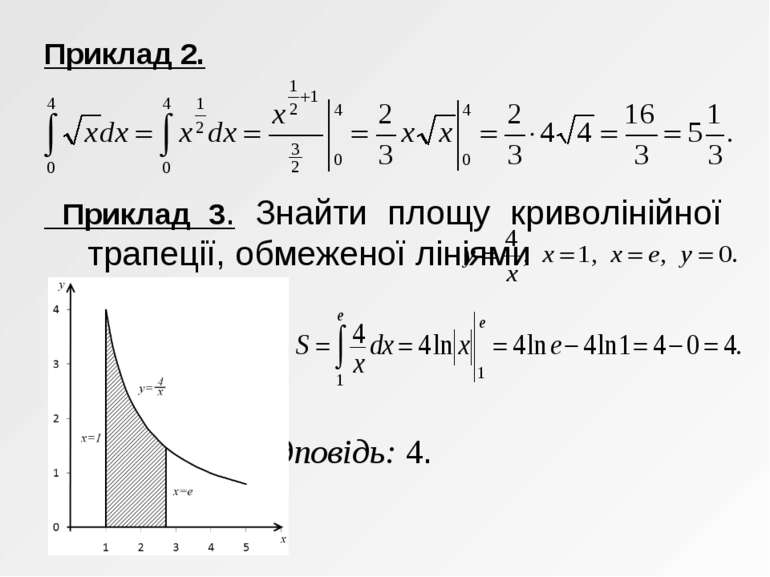
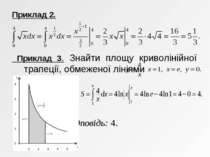
АЛГОРИТМ ЗНАХОДЖЕННЯ ІНТЕГРАЛА ЗА ФОРМУЛОЮ НЬЮТОНА-ЛЕЙБНІЦА знайти будь-яку первісну F функції f на відрізку [a; b]; обчислити значення первісної F у точках x=b та x=a; знайти різницю F(b) – F(a). Приклад 1. Обчислити інтеграл:

Приклад 2. Приклад 3. Знайти площу криволінійної трапеції, обмеженої лініями Відповідь: 4.

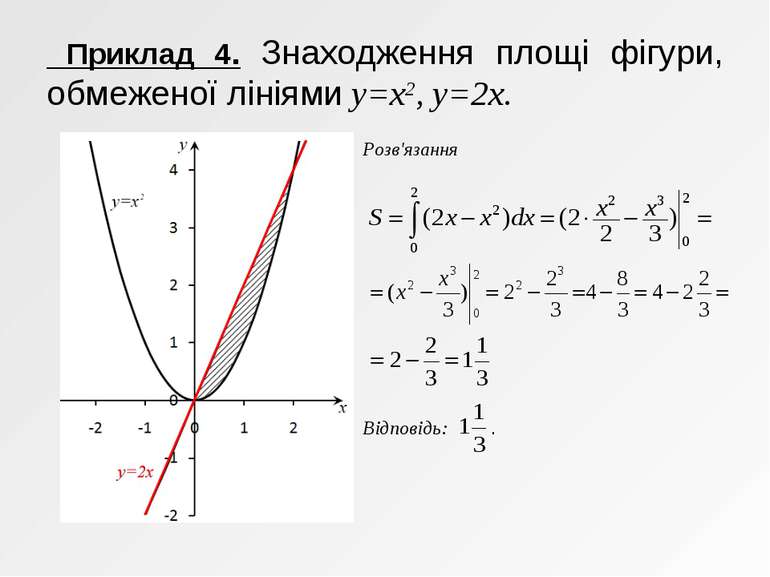
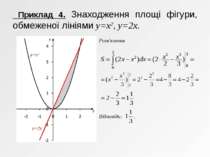
Приклад 4. Знаходження площі фігури, обмеженої лініями y=x2, y=2x. Розв'язання Відповідь: .

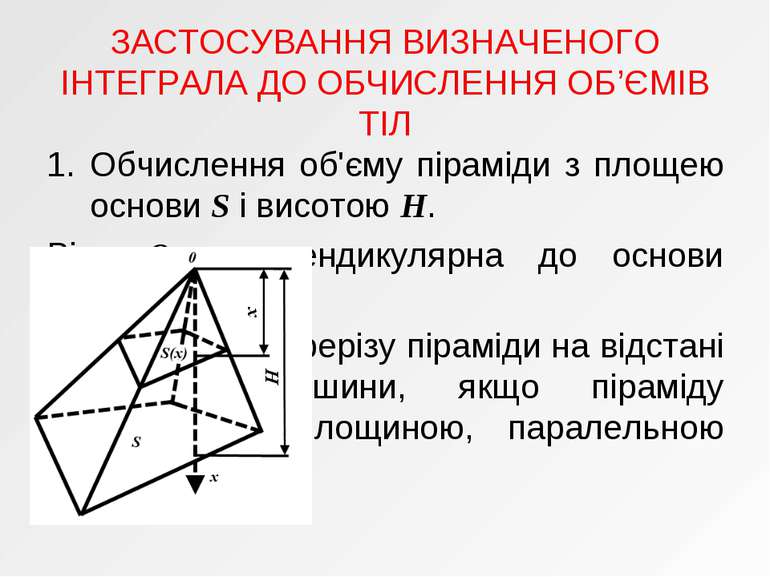
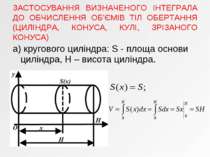
ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДО ОБЧИСЛЕННЯ ОБ’ЄМІВ ТІЛ Обчислення об'єму піраміди з площею основи S і висотою H. Вісь Ox перпендикулярна до основи піраміди. S(x) – площа перерізу піраміди на відстані x від вершини, якщо піраміду перерізати площиною, паралельною основі S.

За властивістю площ подібних фігур:

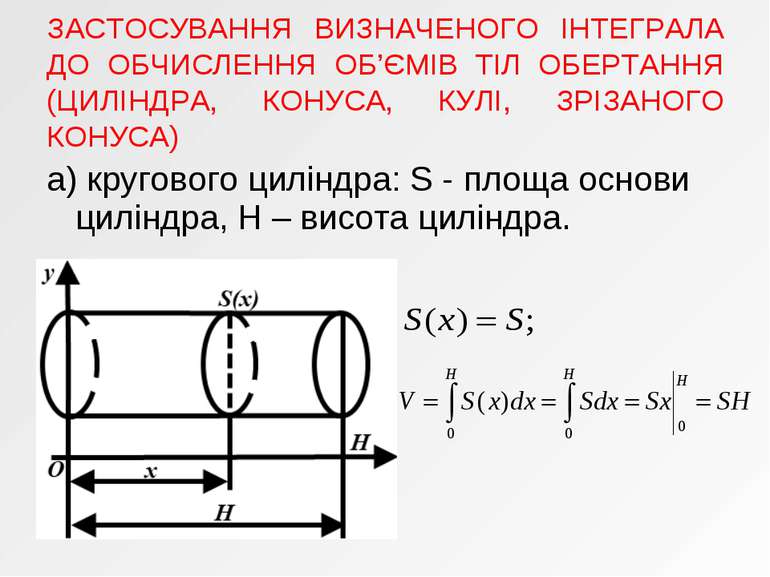
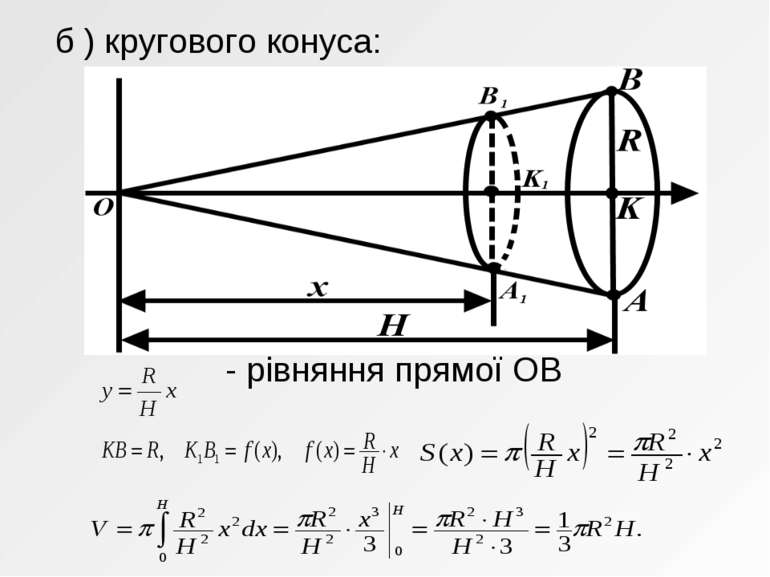
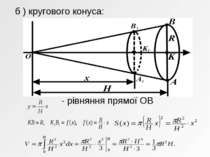
а) кругового циліндра: S - площа основи циліндра, H – висота циліндра. ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДО ОБЧИСЛЕННЯ ОБ’ЄМІВ ТІЛ ОБЕРТАННЯ (ЦИЛІНДРА, КОНУСА, КУЛІ, ЗРІЗАНОГО КОНУСА)

б ) кругового конуса: - рівняння прямої ОВ

Об'єм тіла, утвореного обертанням криволі-нійної трапеції, обмеженої лініями Розв'язання. Формула обчислення об'єму тіла, утвореного обертанням криволінійної трапеції навколо осі Ох: Відповідь: .

Застосування визначеного інтеграла у фізиці Обчислення шляху за відомим законом зміни швидкості. Відомо, що шлях , є первісною для функції , яка виражає закон зміни швидкості. Оскільки шлях, який пройде тіло за інтервал часу від до , є приростом функції , який виражається через інтеграл за формулою Ньютона-Лейбніца, то , за умови, що функція неперервна. Задача. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом (м/с). Знайти шлях, який пройшло тіло за інтервал часу від с до с. Розв'язання. (м) Відповідь: 10 м.

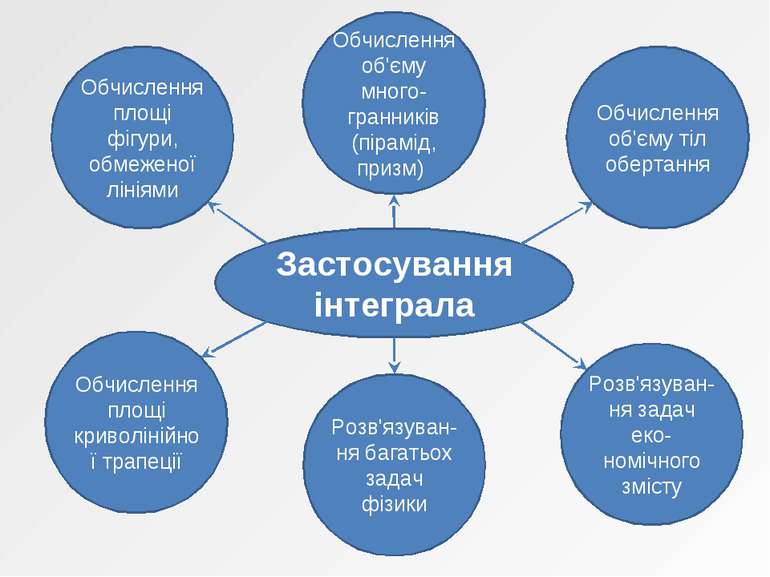
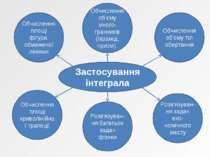
Застосування інтеграла Обчислення площі фігури, обмеженої лініями Обчислення об'єму много-гранників (пірамід, призм) Обчислення об'єму тіл обертання Розв'язуван-ня задач еко-номічного змісту Розв'язуван-ня багатьох задач фізики Обчислення площі криволінійної трапеції

Реклама Я – Інтеграл. Я все можу: обчислити і площу криволінійної трапеції, і площу фігури, обмеженої лініями. А якої популярності я набув при застосуванні до геометрії! При моїй допомозі просто доводять формули обчислення об'єму многогранників, тіл обертання. Застосовують мене до фізики, де я допомагаю знайти формулу шляху за відомим законом зміни швидкості. А яка краса, коли я обчислюю об'єм тіла обертання криволінійної трапеції навколо координатних осей! Незамінним буду я вам і при вивченні багатьох технічних наук. Дякую Ньютону і Лейбніцу, які в свій час зуміли відкрити мої потенціальні можливості. Тому, юні друзі, дружіть зі мною: я постараюсь і надалі служити математичній науці, яка покликана зміцнювати державу, дбати про добробут її громадян. Ваш помічник і сумлінний трудяга Інтеграл.

Методичні рекомендації Слайди 2, 3 використовуються для формування поняття криволінійної трапеції Слайди 4, 5 доцільно використовувати при вивченні матеріалу про площу криволінійної трапеції Слайд 6, 7, 8 використовуються для формування поняття визначеного інтеграла, ознайомлення учнів з формулою Ньютона-Лейбніца Слайди 9, 10 використати при формуванні навичок знаходження площі фігури, обмеженої лініями Слайди 11–14 для формування навичок застосування визначеного інтеграла до виведення формул для обчислення об'єму геометричних тіл. Слайд 15, 16 доцільно застосовувати при систематизації та узагальненні знань учнів про визначений інтеграл.

Список використаної літератури: 1. Мерзляк А.Г. Алгебра. 11 клас: підруч. для загальноосвіт. навчальн. закладів: академ. рівень, проф. рівень / А. Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М. С. Якір. – Х. : Гімназія, 2011. – 431 с.: іл.