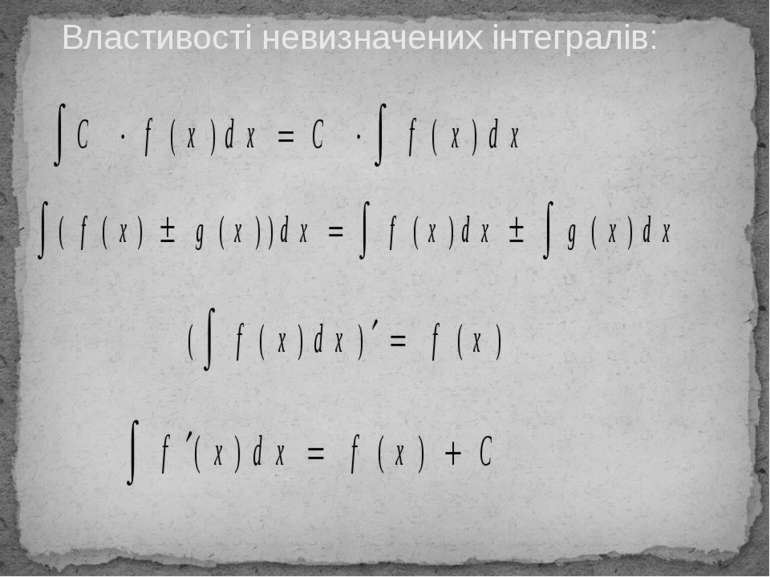Презентація на тему:
Невизначений інтеграл

Невизначений Iнтеграл

Мета Навчитись обчислювати не визначени інтеграли

Історія створення ”інтеграла” Інтеграція простежується ще в давньому Єгипті, приблизно в 1800г. до н. е.., Московський математичний папірус демонструє знання формули об'єму усіченої піраміди. Першим відомим методом для розрахунку інтегралів є метод вичерпання Евдокса (приблизно 370 до н. Е..), Який намагався знайти площі і об'єми, розриваючи їх на нескінченну безліч частин, для яких площа або об'єм вже відомі. Цей метод був підхоплений і розвинутий Архімедом, і використовувався для розрахунку площ парабол і наближеного розрахунку площі круга. Аналогічні методи були розроблені незалежно в Китаї в 3-му столітті н. е..Лю Хуейєм, який використовував їх для знаходження площі круга. Цей метод був згодом використаний Дзю Чонгши для знаходження об'єму кулі. Наступний великий крок на переліку інтегралів був зроблений в Іраку, в XI столітті, математиком Ібн ал-Хайсама (відомим як Alhazen в Європі), у своїй роботі «Про вимір параболічного тіла» він приходить до рівняння четвертого ступеня.

Вирішуючи цю проблему, він проводить обчислення, рівносильні обчислення визначеного інтеграла, щоб знайти обсяг параболоїда.Використовуючи математичну індукцію він зміг узагальнити свої результати для інтегралів від многочленів до четвертого ступеня. Таким чином, він був близький до пошуку загальної формули для інтегралів від поліномів, але він не стосується будь-яких многочленів вище четвертого ступеня. Наступний значний прогрес в обчисленні інтегралів з'явиться лише в XVI столітті.У роботах Кавальєрі з його методом неподільних, а також у роботах Ферма, були закладені основи сучасного інтегрального числення. Подальші кроки були зроблені на початку XVII століття Барроу і Торрічеллі, які представили перші натяки на зв'язок між інтегруванням і диференціюванням.

Функція F (x) називається первообразной для f (x) що визначена на деякому проміжку a, b, якщо для кожного х з цього проміжку виконуються умови Безліч первісних для f (x) називається невизначеним інтегралом для f (x) дх функція F (x ) Називається первообразной для f (x) що визначена на деякому проміжку a, b, якщо для кожного х з цього проміжку виконуються умови

Властивості невизначених інтегралів:

Таблиця невизначених інтегралив

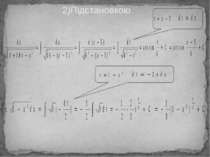
Методи знаходження невізначених інтегралів: 1)За табліцею: підінтегральна функція зводится до табличного вигляду за допомогою тотожніх пересворень.

2)Підстановкою

3)За частинами Типи інтегралів до яких застосовуются формули

Презентацію підготували студенти групи ОТ-110, Лєбов та Єннан