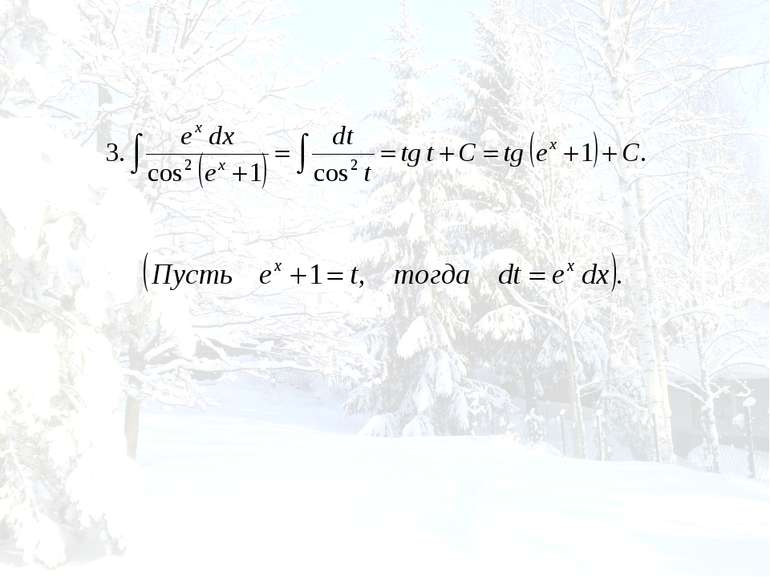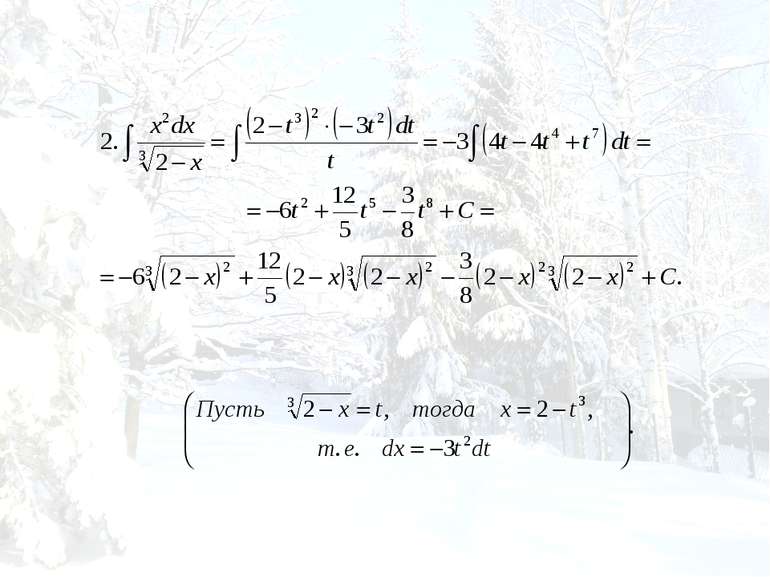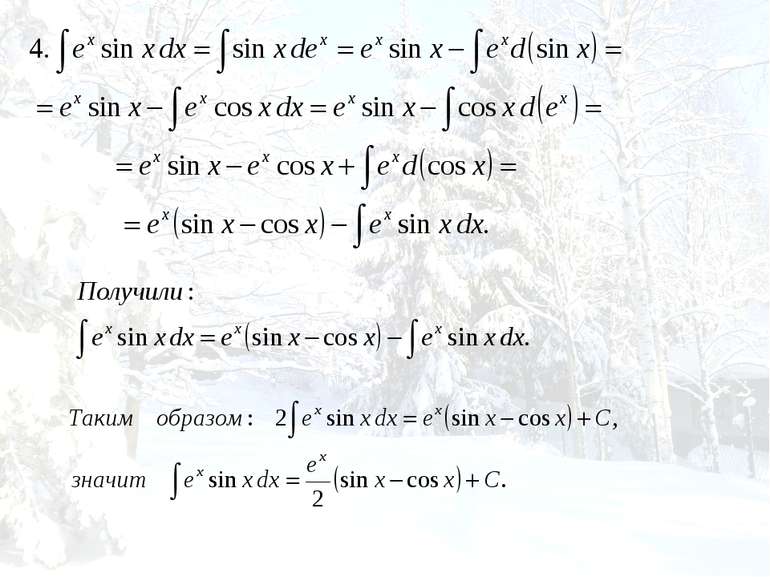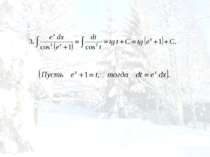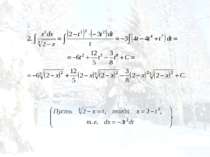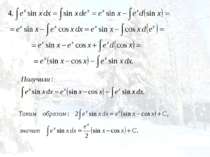Презентація на тему:
Первісна та невизначений інтеграл

Как называется раздел математики, в котором изучаются производные и их применение к исследованию функции?

Сформулируйте основную задачу дифференциального исчисления?

Приходится часто решать и обратную задачу… По данной функции f (х) требуется найти функцию F (х) такую ,что F' (х)=f (х) Пример из механики. Если в начальный момент времени t=0, v(t)=0 то при свободном падении S(t)=gt² ⁄ 2 - эта формула была получена Галилеем эксперементально.

«Интеграл» - латинское слово integro – “восстанавливать” или integer – “целый”. Одно из основных понятий математического анализа, возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным. Впервые это слово употребил в печати швецкий ученый Я. Бернулли (1690 г.).

« Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.» Лейбниц

Исаак Ньютон (1643-1727)

дифференцирование интегрирование

Обозначения:

Понятие первообразной Функцию F(x) называют первообразной для функции f(x) на интервале (a; b), если на нем производная функции F(x) равна f(x): Операцию, обратную дифференцированию называют интегрированием.

совокупность первообразных

Примеры f(x) = 2x; F(x) = x2 F (x)= (x2) = 2x = f(x) f(x) = – sin x; F(x) = сos x F (x)= (cos x) = – sin x = f(x) f(x) = 6x2 + 4; F(x) = 2x3 + 4x F (x)= (2x3 + 4x) = 6x2 + 4 = f(x) f(x) = 1/cos2 x; F(x) = tg x F (x)= (tg x) = 1/cos2 x= f(x)

Неопределенный интеграл Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x) называют совокупность её первообразных функций. где f(x) – подинтегральная функция, f(x)dx – подинтегральное выражение (дифференциал), с – постоянная интегрирования.

Три правила нахождения первообразных 1º Если F(x) есть первообразная для f(x), а G(x) – первообразная для g(x), то F(x) + G(x) есть первообразная для f(x) + g(x). 2º Если F(x) есть первообразная для f(x), а k – постоянная, то функция kF(x) есть первообразная для kf.

Основные свойства неопределенного интеграла.

Примеры

Таблица первообразных f(x) F(x) F(x)

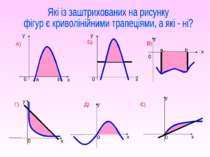
Площадь фигуры Объем тела вращения Работа переменной силы Работа электрического заряда Центр масс Формула энергии заряженного конденсатора Гармонические колебания Экономическое содержание интеграла Задача о радиоактивном распаде Задача о размножении бактерий

Я.Каменский Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию.

Табличный. Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. Интегрирование с помощью замены переменной (подстановкой). Интегрирование по частям.

Нахождение интеграла методом преобразования подынтегральной функции в сумму или разность.

Метод замены переменной

Интегрирование методом замены переменной.

Интегрирование выражений, содержащих радикалы, методом подстановки.

Интегрирование функций, содержащих квадратный трехчлен

Пример

Интегрирование алгебраических дробей.

Интегрирование по частям

Примеры

Примеры

Пример Найти

Интегрирование по частям.

Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше. Э. Золя.