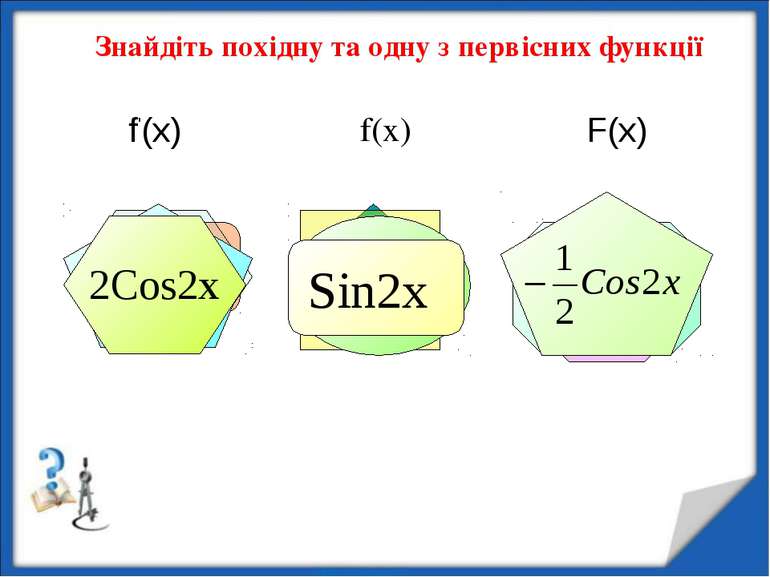
Презентація на тему:
площа трапеції

Знайдіть похідну та одну з первісних функції 0 f'(x) f(x) F(x)

y y y y x x x x 1. 4. 3. 2. На якому рисунку зображена криволінійна трапеція?

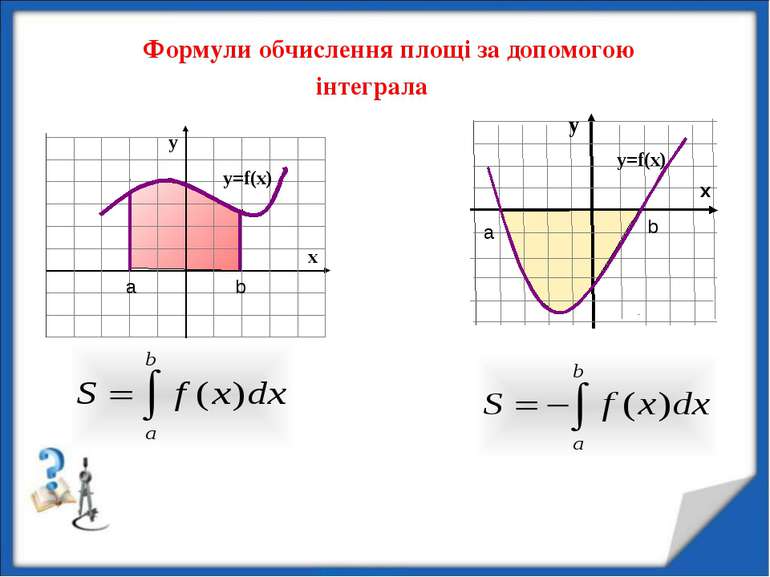
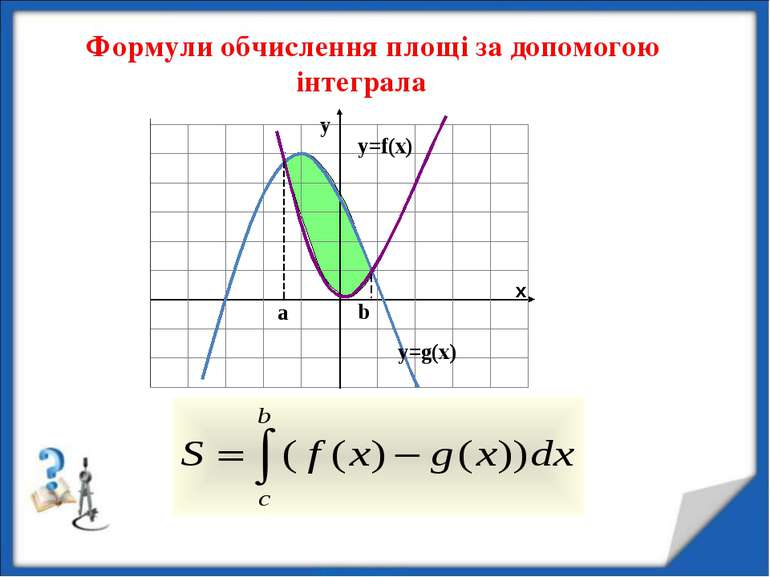
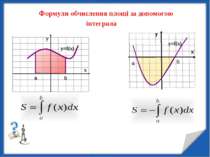
Формула обчислення площі з допомогою інтеграла Нехай функція f(x) неперервна на відрізку [а;b] і нехай F(х) яка– небудь ії первісна. Тоді справедли ва рівність формула Ньютона-Лейбніца

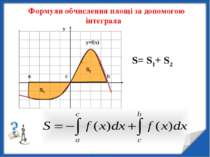
ПРО ІНТЕГРАЛ МОЖНА СКАЗАТИ: ІНТЕГРАЛ – ПЛОЩА Площа криволінійної трапеції знаходиться за формулою Ньютона-Лейбніца

Формули обчислення площі за допомогою інтеграла

Формули обчислення площі за допомогою інтеграла х S= S1+ S2

Формули обчислення площі за допомогою інтеграла x

Знайдіть площу фігури, обмежену лініями у = х2 + 2, х = 1, х = -2 у S = 9 ед.кв

х у = х2 - 3 Знайдіть площу фігури, обмежену лініями у = х - 3, у = х2 -3

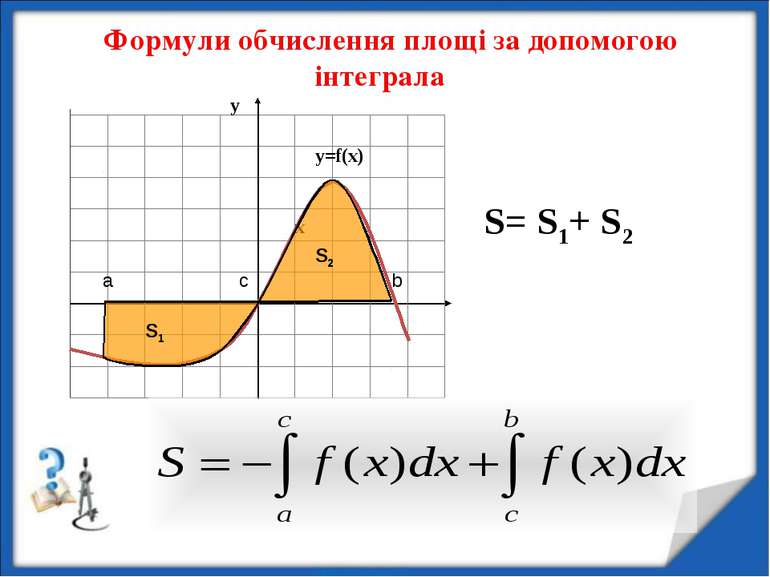
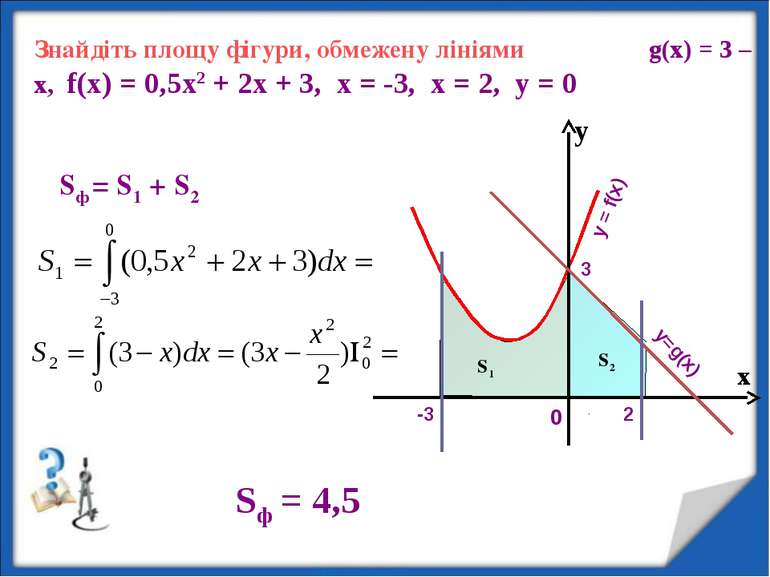
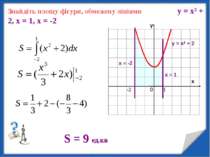
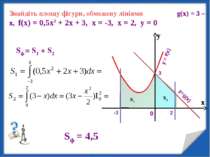
Знайдіть площу фігури, обмежену лініями g(x) = 3 – х, f(x) = 0,5х2 + 2х + 3, х = -3, х = 2, у = 0 у х S1 S2 Sф = S1 + S2 Sф = 4,5

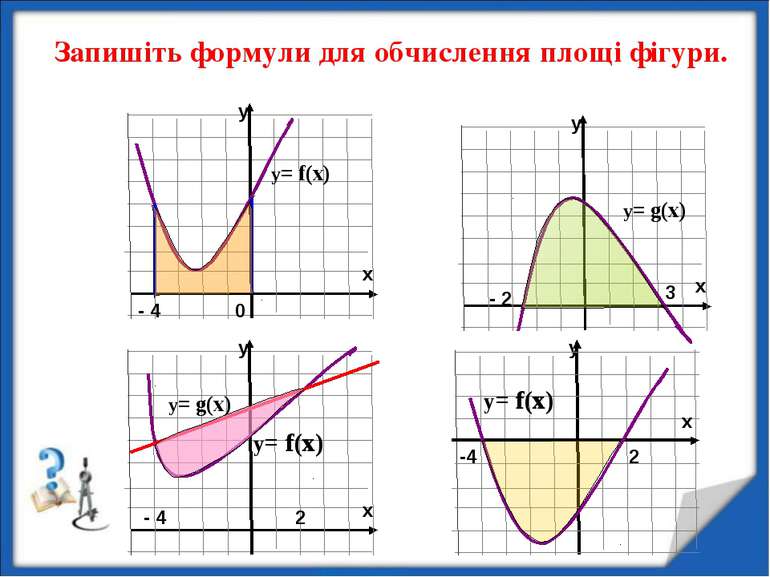
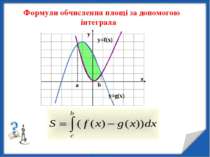
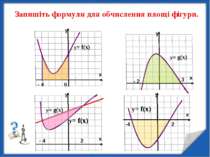
y Запишіть формули для обчислення площі фігури. y= f(x) y= f(x) -4 2 - 2 3 0 - 4 2 - 4 y= g(x) y= g(x) y= f(x)

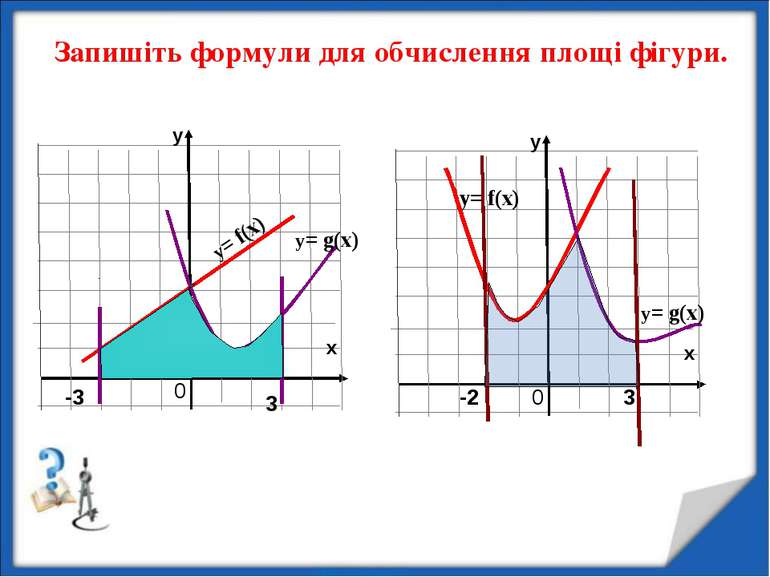
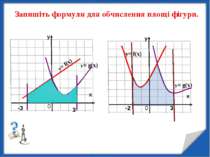
y= f(x) y= f(x) y= g(x) -3 3 0 Запишіть формули для обчислення площі фігури. y= g(x) -2 3 0

Федотова Тамара Валентиновна ДЯКУЄМО ЗА УВАГУ!