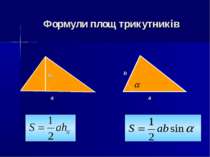
Презентація на тему:
Площа фігур
Завантажити презентацію
Площа фігур
Завантажити презентаціюПрезентація по слайдам:
Дану презентацію рекомендуємо використовувати при узагальненні вивчення теми “Площі фігур” Вона розбита на дві теми “Площа чотирикутника” і “Площа трикутника” Міститься додаткова інформація в темі “Сторінка ерудита ”
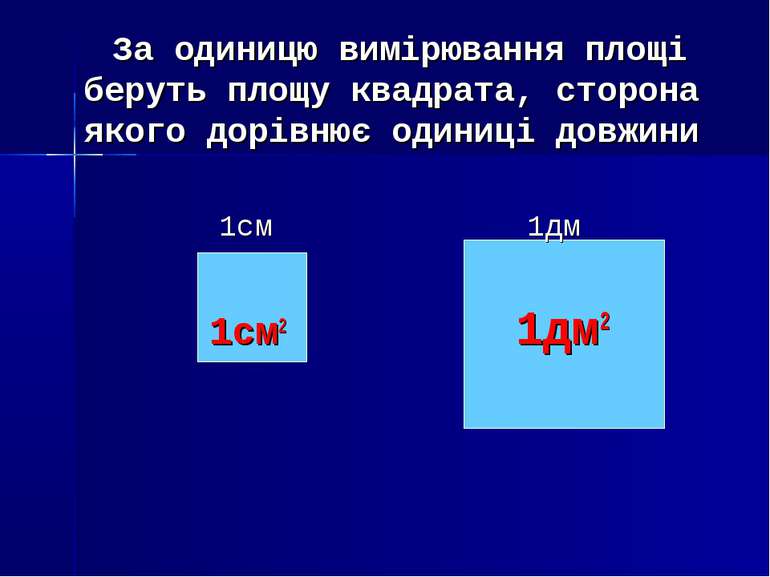
За одиницю вимірювання площі беруть площу квадрата, сторона якого дорівнює одиниці довжини 1см 1дм 1см2 1дм2
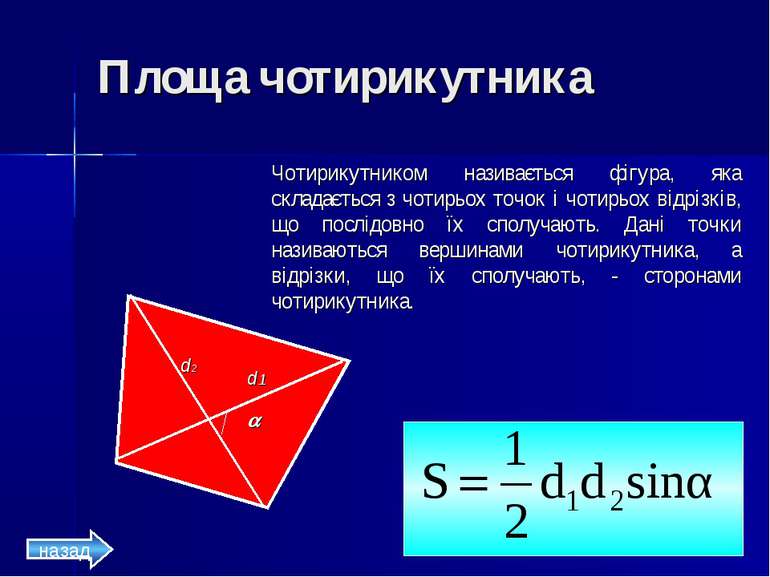
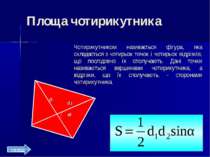
Площа чотирикутника Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. Дані точки називаються вершинами чотирикутника, а відрізки, що їх сполучають, - сторонами чотирикутника. d2 d1 назад
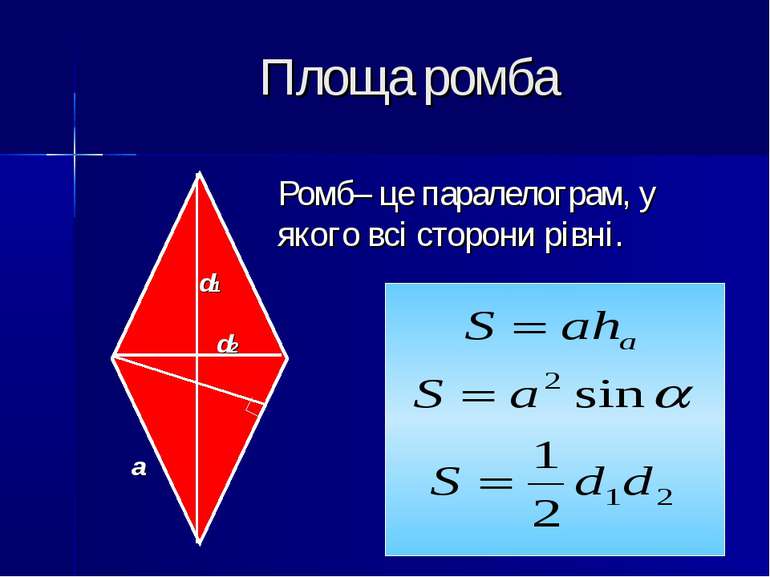
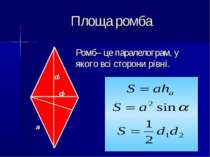
Площа паралелограма Паралелограм – це чотирикутник, у якого протилежні сторони паралельні, тобто лежать на паралельних прямих ha a назад
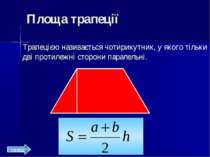
Площа трапеції Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. назад
Сторінка ерудита Правильний сімнадцятикутник Правильний сімнадцятикутник — геометрична фігура, що належить до групи правильних багатокутників. Він має сімнадцять сторін та сімнадцять кутів, всі його кути та сторони рівні між собою, всі вершини лежать на одному колі. Правильний сімнадцятикутник можна побудувати за допомогою циркуля та лінійки, що було доведено Гаусом у 1796 році. Ним же знайдено значення косинуса центрального кута сімнадцятикутника:
У 1825 році Йоханес Ерхінгер вперше опублікував детальний опис побудови правильного сімнадцятикутника за 64 кроки.
257-кутник У графічному зображенні правильний 257-кутник майже не відрізняється від кола 257-кутник можна побудувати при обмеженому наборі інструментів лише циркулем та лінійкою. Число 257 — одне з п'яти відомих простих чисел Ферма Карл Фрідріх Гаус у 1836 році довів, що багатокутник можна побудувати за допомогою циркуля та лінійки, якщо число його вершин рівне простому числу Ферма. Керівництво з побудови 257-кутника вперше було запропоноване Фрідріхом Юліусом Рішело у 1832 році. У 1991 році Дюан Детампль запропонував варіант побудови з використанням 150-ти допоміжних кіл назад
Використнані матеріали: http://www.uk.wikipedia.org/ http://www.fdp-ipsa.ntu-kpi.kiev.ua/ Karin Reich (1825). В кн.: Mathesis, Festschrift zum siebzigsten Geburtstag von Matthias Schramm. Hrsg. von Rüdiger Thiele, Berlin, Diepholz 2000, стр. 101—118. Підручник “Геометрія 9 клас”, О.В.Погорелов http://www.uk.wiktionary.org/
Презентацію підготували: Малиш С., Оліференко Е., Хольченков А. учні 10-б класу, СЗОШ №2 вчитель математики: Бугайова О.В.
Схожі презентації
Категорії