Презентація на тему:
Площа паралелограма та трикутника

Теорема:Площа паралелограма дорівнює добутку його сторони і висоти,яка відповідає цій стороні Дано:ABCD-пар-м; BM,CN-висоти Довести: Sпар-ма= = BM*BC Доведення Площа паралелограма дорівнює сумі площ трикутника ABM і трапеції MBCD. Площа прямокутника дорівнює сумі площ трапеції BMDC і трикутника DCN.Проте трикутник ABM =трикутнику DCN за гіпотенузою і гострим кутом (відрізки AB і CD рівні як протилежні сторони паралелограма, кути BAM і CDN рівні як відповідні при паралельних прямих AB і DC та січній AD). Отже, ці трикутники рівновеликі. Звідси випливає,що пар-м ABCD і прямокутник MBCN рівновеликі. За теоремою про площу прямокутника слідує, що площа прямокутника MBCN дорівнює добутку BM*BC.Тоді S=BM*BC, де S-площа паралелограма ABCD,що й треба було довести. А D N B C M

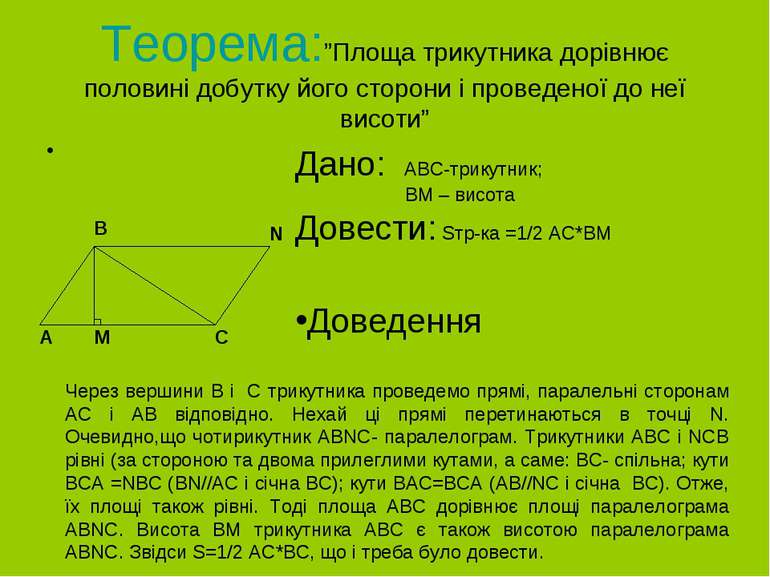
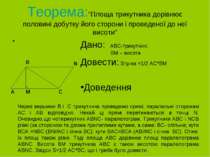
Теорема:”Площа трикутника дорівнює половині добутку його сторони і проведеної до неї висоти” M B A C N Дано: ABC-трикутник; BM – висота Довести: Sтр-ка =1/2 AC*BM Доведення Через вершини B і C трикутника проведемо прямі, паралельні сторонам AC і AB відповідно. Нехай ці прямі перетинаються в точці N. Очевидно,що чотирикутник ABNC- паралелограм. Трикутники ABC і NCB рівні (за стороною та двома прилеглими кутами, а саме: BC- спільна; кути BCA =NBC (BN//AC і січна BC); кути BAC=BCA (AB//NC і січна BC). Отже, їх площі також рівні. Тоді площа ABC дорівнює площі паралелограма ABNC. Висота BM трикутника ABC є також висотою паралелограма ABNC. Звідси S=1/2 AC*BC, що і треба було довести.

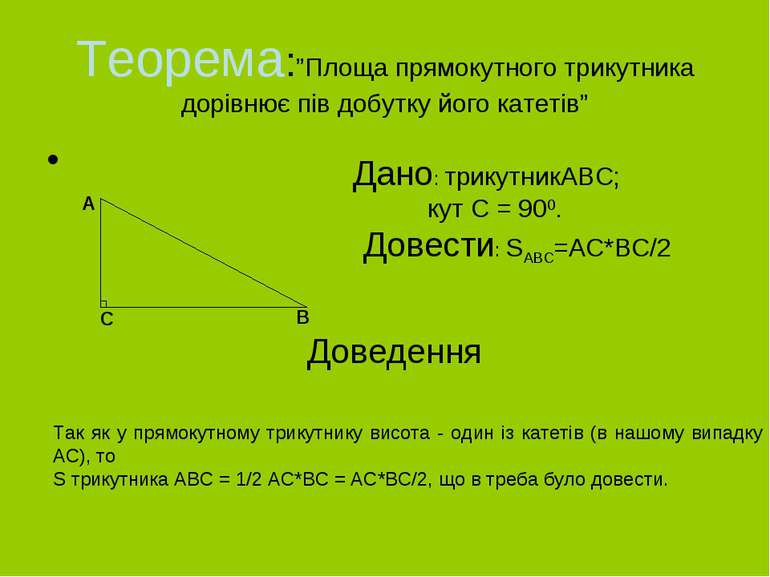
Теорема:”Площа прямокутного трикутника дорівнює пів добутку його катетів” C A B Дано: трикутникABC; кут C = 900. Довести: SABC=AC*BC/2 Доведення Так як у прямокутному трикутнику висота - один із катетів (в нашому випадку AC), то S трикутника ABC = 1/2 AC*BC = AC*BC/2, що в треба було довести.

Задачі 1) Знайти площу паралелограма, сторона якого дорівнює 15 см, а висота проведена до цієї сторони дорівнює 7 см. B C A D Дано: ABCD - паралелограм; AD = 15 см; BH = 7 см Знайти: SABCD. Розв’язання: H 1)Розв’яжемо задачу за формулою площі паралелограма: S ABCD= BH*AD, підставимо у формулу числа: S ABCD = 7*15 = 105 (cм2) Відповідь: 105 см2.

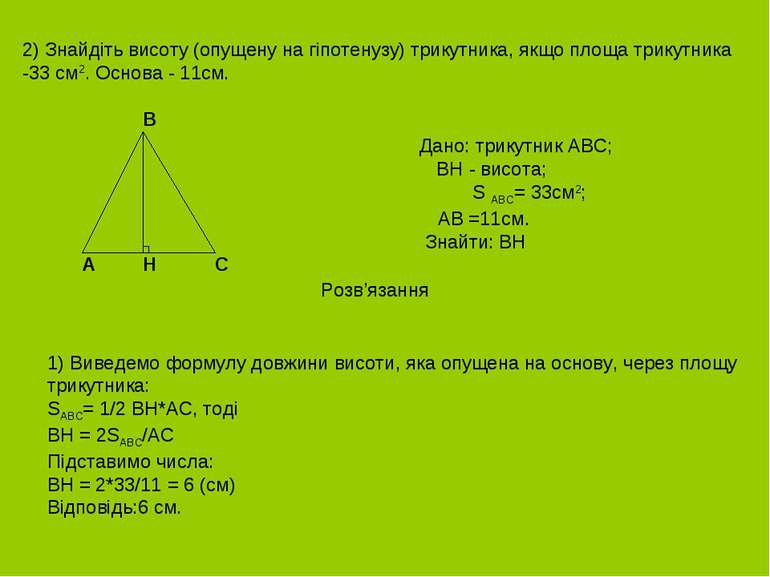
2) Знайдіть висоту (опущену на гіпотенузу) трикутника, якщо площа трикутника -33 см2. Основа - 11см. A B C H Дано: трикутник ABC; BH - висота; S ABC= 33см2; AB =11см. Знайти: BH Розв’язання 1) Виведемо формулу довжини висоти, яка опущена на основу, через площу трикутника: SАВС= 1/2 BH*AC, тоді BH = 2SАВС/AC Підставимо числа: BH = 2*33/11 = 6 (см) Відповідь:6 см.

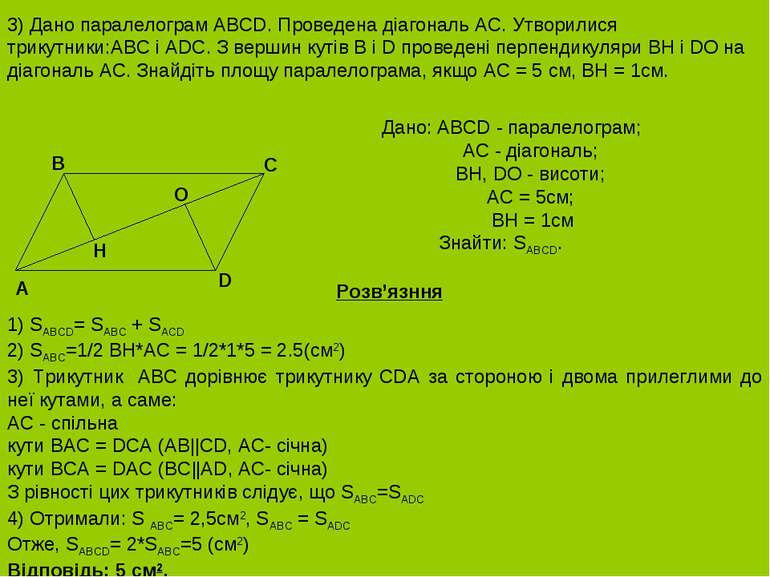
3) Дано паралелограм ABCD. Проведена діагональ AC. Утворилися трикутники:ABC і ADC. З вершин кутів B і D проведені перпендикуляри BH і DO на діагональ AC. Знайдіть площу паралелограма, якщо AC = 5 см, BH = 1см. Дано: ABCD - паралелограм; AC - діагональ; BH, DO - висоти; AC = 5см; BH = 1см Знайти: SABCD. A B D C H O Розв’язння 1) SABCD= SABC + SACD 2) SABC=1/2 BH*AC = 1/2*1*5 = 2.5(см2) 3) Трикутник ABC дорівнює трикутнику CDА за стороною і двома прилеглими до неї кутами, а саме: AC - спільна кути BAC = DCА (AB||CD, AC- січна) кути BCA = DAC (BC||AD, AC- січна) З рівності цих трикутників слідує, що SАВС=SADC 4) Отримали: S ABC= 2,5см2, SABC = SADC Отже, SABCD= 2*SABC=5 (см2) Відповідь: 5 см2.

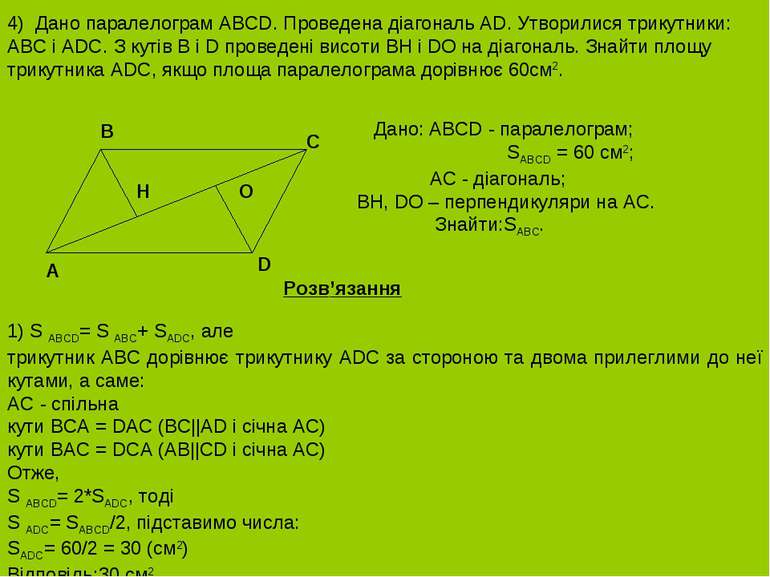
4) Дано паралелограм ABCD. Проведена діагональ AD. Утворилися трикутники: ABC і ADC. З кутів B і D проведені висоти BH і DO на діагональ. Знайти площу трикутника ADC, якщо площа паралелограма дорівнює 60см2. Дано: ABCD - паралелограм; SABCD = 60 см2; AC - діагональ; BH, DO – перпендикуляри на АС. Знайти:SАВС. A B C D H O Розв’язання 1) S ABCD= S ABC+ SADC, але трикутник ABC дорівнює трикутнику ADC за стороною та двома прилеглими до неї кутами, а саме: AC - спільна кути BCA = DAC (BC||AD і січна AC) кути BAC = DCA (AB||CD і січна AC) Отже, S ABCD= 2*SADC, тоді S ADC= SABCD/2, підставимо числа: SADC= 60/2 = 30 (см2) Відповідь:30 см2.

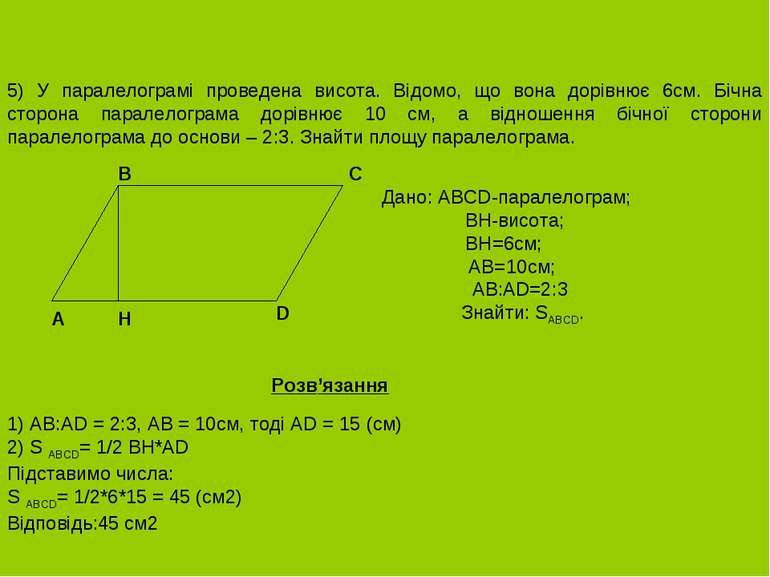
5) У паралелограмі проведена висота. Відомо, що вона дорівнює 6см. Бічна сторона паралелограма дорівнює 10 см, а відношення бічної сторони паралелограма до основи – 2:3. Знайти площу паралелограма. Дано: ABCD-паралелограм; BH-висота; BH=6см; AB=10см; AB:AD=2:3 Знайти: SABCD. A B C D H Розв’язання 1) AB:AD = 2:3, AB = 10см, тоді AD = 15 (см) 2) S ABCD= 1/2 BH*AD Підставимо числа: S ABCD= 1/2*6*15 = 45 (см2) Відповідь:45 см2

6) В прямокутному трикутнику гіпотенуза дорівнює 10см, а більший катет – 8см. Знайти площу трикутника. Дано: трикутник ABC; кут C = 900; AB=10см; BC=8см. Знайти: S трикутника ABC Розв’язання C A B 1) Для трикутника ABC за теоремою Піфагора: AC2 = AB2 – BC2 Підставимо числа: 2) . Підставимо числа: Відповідь: 24 см2.