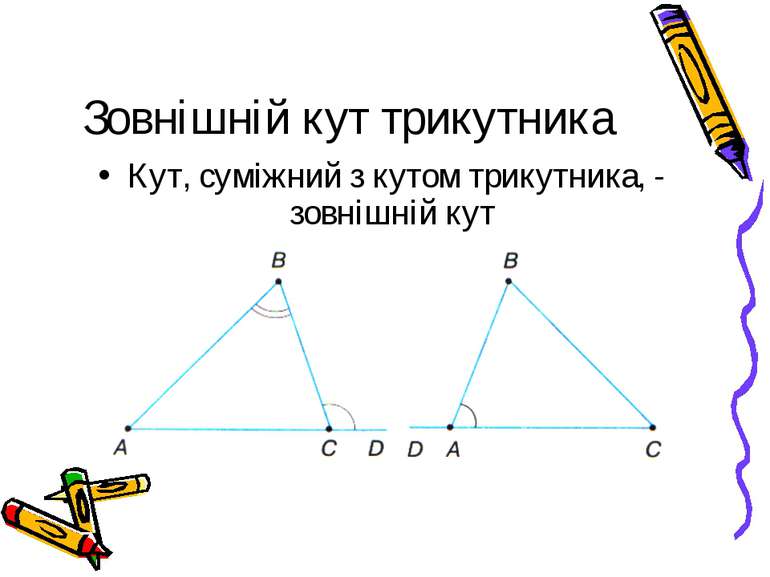
Презентація на тему:
Властивості кутів трикутника

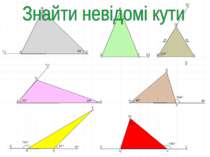
Властивості кутів трикутника 1 Група Намалювати довільний трикутник, позначити його елементи та за допомогою транспортира виміряти його кути. Знайти їх суму. Порівняти свої дані з даними однокласників. Зробити висновок 2 Група У програмі геометрія намалювати довільний трикутник, виміряти його кути. Знайти їх суму. Порівняти свої дані з даними однокласників. Зробити висновок

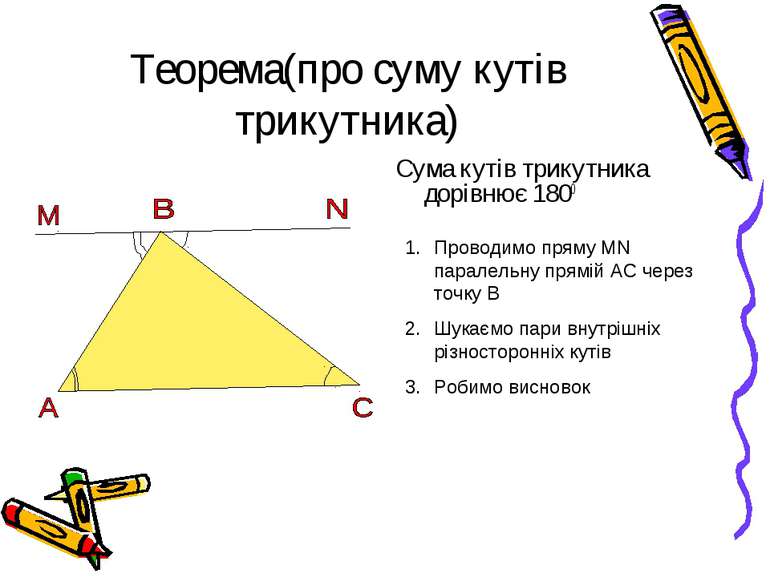
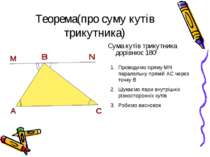
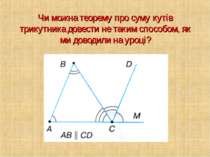
Теорема(про суму кутів трикутника) Сума кутів трикутника дорівнює 1800 Проводимо пряму MN паралельну прямій АС через точку В Шукаємо пари внутрішніх різносторонніх кутів Робимо висновок

Дайте відповідь на запитання та обґрунтуйте свою відповідь Чи може трикутник мати один прямий кут? Як називається такий трикутник? Чи може трикутник мати дві пари прямих кутів? Чи може трикутник мати один тупий кут? Як називається такий трикутник? Чи може трикутник мати два тупих кути? Якщо в трикутнику один з кутів прямий або тупий, то якого виду інші два його кути?

Наслідки Трикутник може мати лише один прямий або тупий кут. Якщо один із кутів трикутника прямий або тупий, то два інші кути – гострі. Сума гострих кутів прямокутного трикутника дорівнює 900

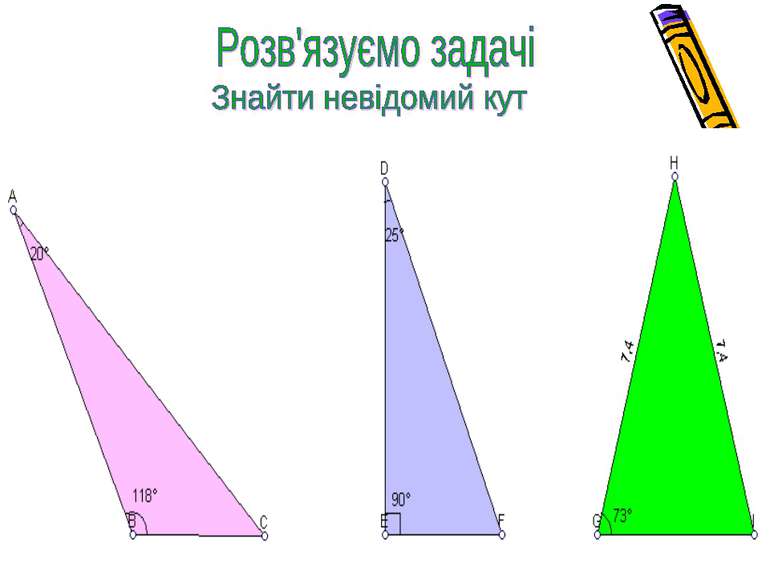
Кут 1 – на 120 більший Кут 2 у 3 рази більший Кут 3 Знайти градусні міри кутів трикутника, якщо вони відносяться як 1:3:5

Намалюйте довільний трикутник та продовжіть будь-яку з його сторін

Зовнішній кут трикутника Кут, суміжний з кутом трикутника, - зовнішній кут

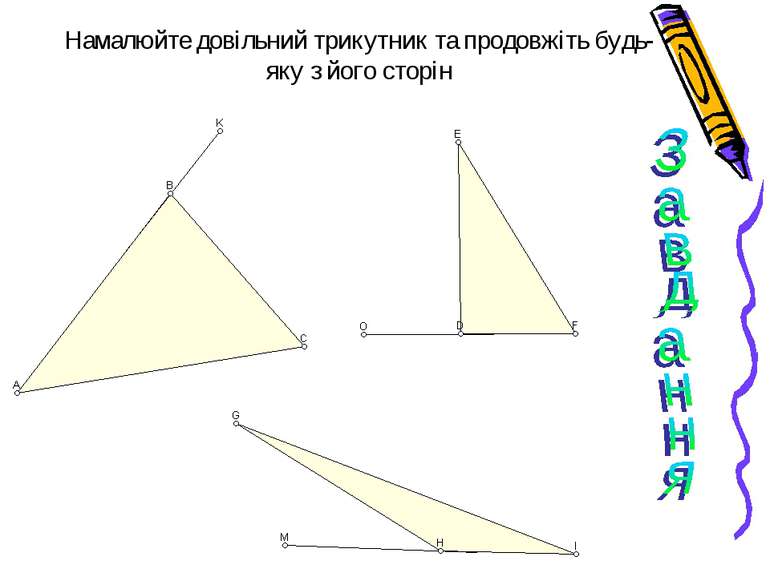
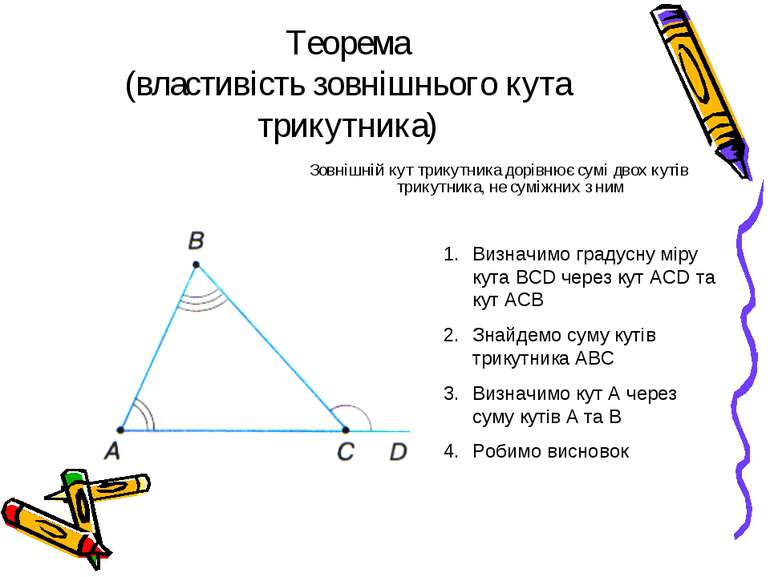
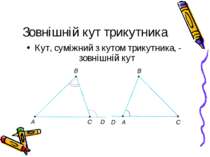
Теорема (властивість зовнішнього кута трикутника) Зовнішній кут трикутника дорівнює сумі двох кутів трикутника, не суміжних з ним Визначимо градусну міру кута BCD через кут ACD та кут АСВ Знайдемо суму кутів трикутника АВС Визначимо кут А через суму кутів А та В Робимо висновок

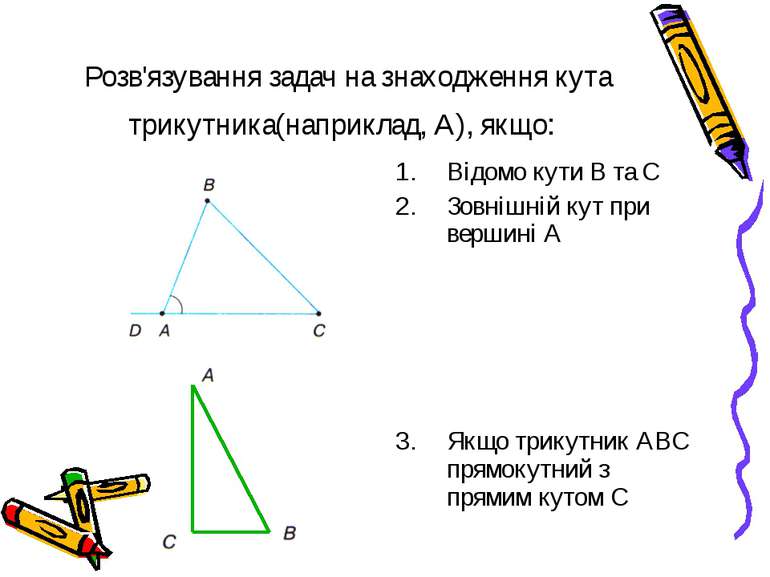
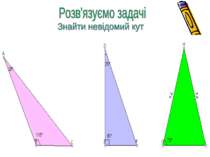
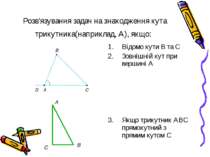
Розв'язування задач на знаходження кута трикутника(наприклад, А), якщо: Відомо кути В та С Зовнішній кут при вершині А Якщо трикутник АВС прямокутний з прямим кутом С

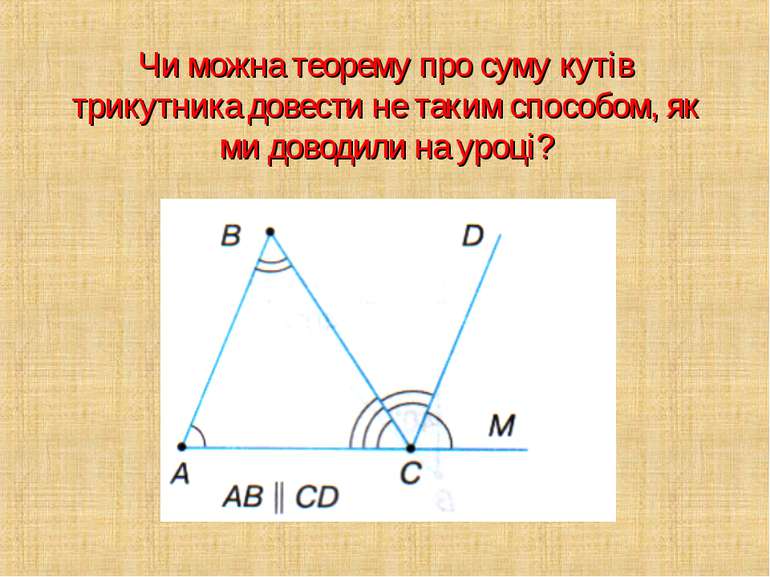
Чи можна теорему про суму кутів трикутника довести не таким способом, як ми доводили на уроці?

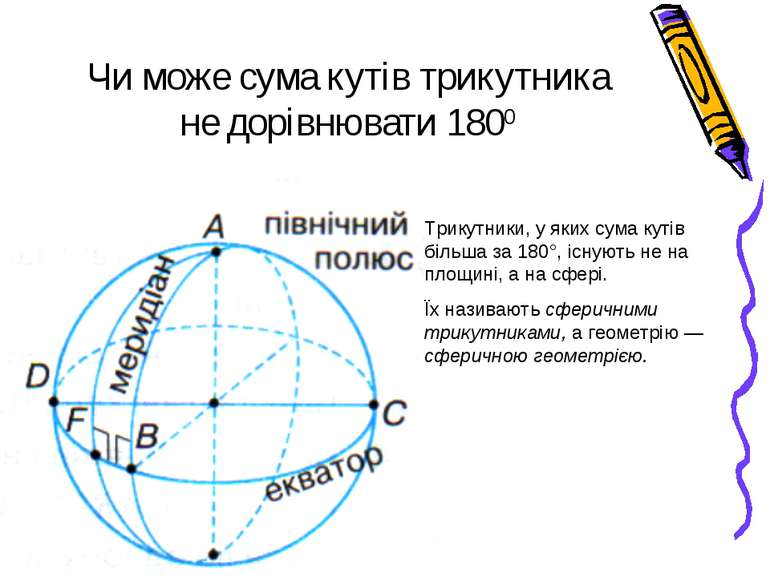
Чи може сума кутів трикутника не дорівнювати 1800 Трикутники, у яких сума кутів більша за 180°, існують не на площині, а на сфері. Їх називають сферичними трикутниками, а геометрію — сферичною геометрією.

Земна поверхня має форму сфери Найкоротша лінія між двома точками на площині — пряма, а на сфері вона крива. Якщо із кривих ліній утворити трикутники, то сума їх кутів буде більшою за 180°. Звичайно, це стосується великих за розмірами трикутників. Наприклад, розглянемо трикутник, у якого вершина А — на північному полюсі, а вершини В і F— на екваторі. Тоді кожний з кутів при вершинах В і F дорівнюватиме 90°. Отже, сума кутів трикутника АBF більша за 180°. Подивіться на глобус і знайдіть ще які-небудь сферичні трикутники. Науку, яка займається вимірюванням Землі та способами зображення її поверхні, називають геодезією.

Карл Фрідріх Гаус (1777-1855) Учений захопився старою, як світ, загадкою евклідового постулату про паралельні прямі. У 1818 році Гаус здогадався, що цей постулат може мати інше формулювання " але не на площині, а на інших поверхнях, невідомих Евкліду.

Народився в сім'ї дрібного чиновника. Майже все життя провів у Казані. Там 1802—1807 навчався в гімназії за державний кошт. 1807—1811 навчався в Казанському університеті. Ректор Казанського університету (1827-1846). Відкритття Лобачевського (1826, опубліковані 1829-1930) здійснили переворот в уявленнях про природу простору, в основі яких більше 2 тисяч років лежало вчення Евкліда. Йому належать також праці з алгебри, математичного аналізу, терії ймовірностей, механіки, фізики та астрономії. Мико ла Іва нович Лобаче вський (20 листопада (1 грудня) 1792, Нижній Новгород — †12 лютого (24 лютого) 1856, Казань) — російський математик, творець неевклідової геометрії. Геометрія з багатьма прямими, що проходять через одну точку і не перетинають дану пряму називають геометрією Лобачевського.