Презентація на тему:
Градусна і радіанна міри кутів

Градусна і радіанна міри кутів Робота студенток групи Б50/9-11 Камінської Олени Красюн Тетяни

Градусна міра кута

Д Р Е В Н І Й В А В І Л О н

Ще в Древньому Вавілоні за довго до нашої ери жерці вважали, що свій денний шлях сонце проходить за 180 кроків, а значить один крок складає 1/180 розгорнутого кута. У Вавілоні була прийнята шестидесятирічна система числення, тобто фактично числа записувались у вигляді суми степенів числа 60, а не 10. Тому зрозуміло, що для більш мілких одиниць вимірювання кутів один “крок ” послідовно ділиться на 60 частин. А саме слово “градус” походить від латинського gradus (крок, сходинка). Секунда перекладається як “друга”.

π Майже за 3 тис. років до н.е. у Вавілоні був календар, отже велись астрономічні обчислення, які неможливі без тригонометричних розрахунків

Радіанна міра кута

Інша одиниця вимірювання кутів - радіанна введена зовсім недавно. Перше видання (це були екзаменаційні білети), що містили термін “радіан” з’явилось в 1873р. в Англії. Сам термін “радіан” походить від латинського radius (спиця, промінь). А Н Г Л І я

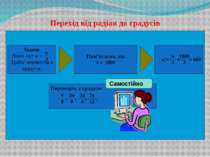
При радіанному вимірюванні за одиницю вимірювання беруть радіан – дугу, довжина якої дорівнює радіусу цієї дуги. Радіанну міру дуги обчислюють за формулою , де α - радіанна міра дуги, l- довжина дуги кола, r - радіус цієї дуги. Градусна міра одного радіана дорівнює 57˚17′44″,8 Радіанна міра розгорнутого кута дорівнює π, тобто π=180˚

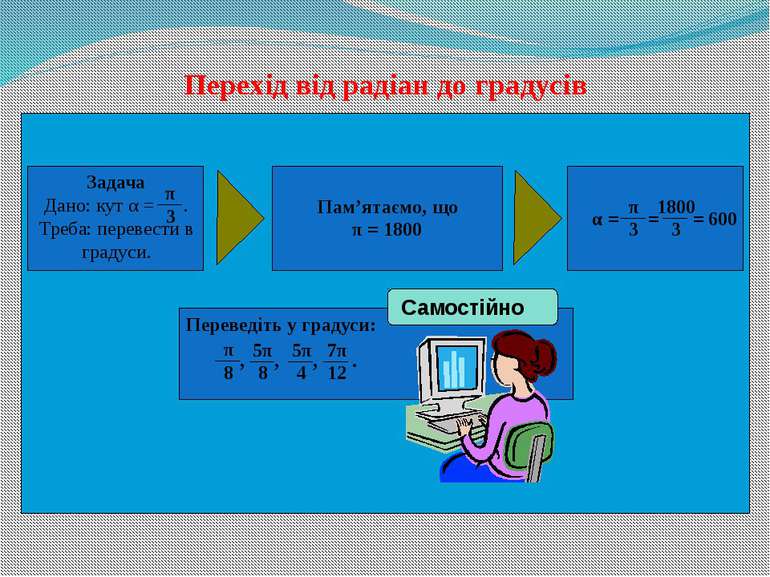
Формула переходу від градусної міри до радіанної де α˚ - градусна міра дуги (кута). Радіанна міра одного градуса дорівнює 0,0175 радіана. До речі: радіан не має ніяких позначень; наприклад, запис sin 2 означає “синус двох радіан”, а запис sin 20 означає “синус двох градусів”.

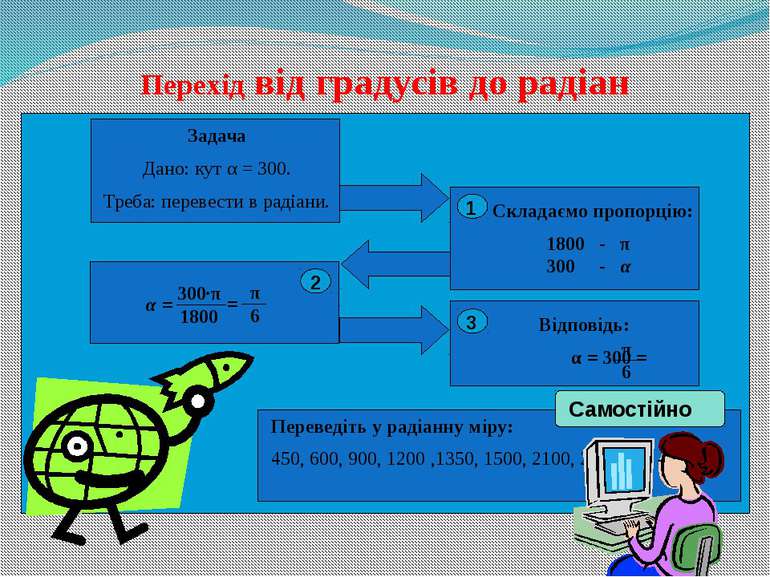
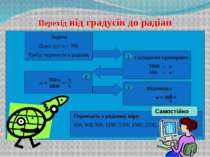
Перехід від градусів до радіан Задача Дано: кут α = 300. Треба: перевести в радіани. Складаємо пропорцію: 1800 - π 300 - α 1 2 α = 300∙π 1800 = π 6 Відповідь: α = 300 = 3 π 6 Переведіть у радіанну міру: 450, 600, 900, 1200 ,1350, 1500, 2100, 2400. Самостійно

Формула переходу від радіанної міри до градусної

Перехід від радіан до градусів Переведіть у градуси: Самостійно

Різні співвідношення відрізків трикутника та кола зустрічаються вже в III ст. до нашої ери в роботах великих математиків Древньої Греції – Евкліда, Архімеда, Аполонія Пергського

Поняття одиничного кола

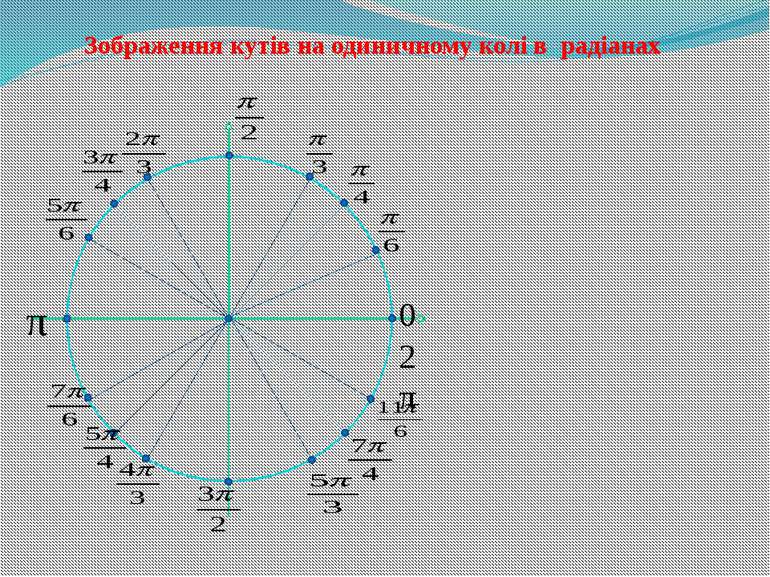
Кожному дійсному числу α на колі відповідає точка Pα, яку дістаємо з точки Pо кола з координатами (1;0) переміщенням вздовж кола на відстань α проти руху годинникової стрілки при α >0 і на відстань α за рухом годинникової стрілка, при α < 0 . Одиничне коло Одиничним колом називається коло з центром у початку координат і радіусом рівним одиниці

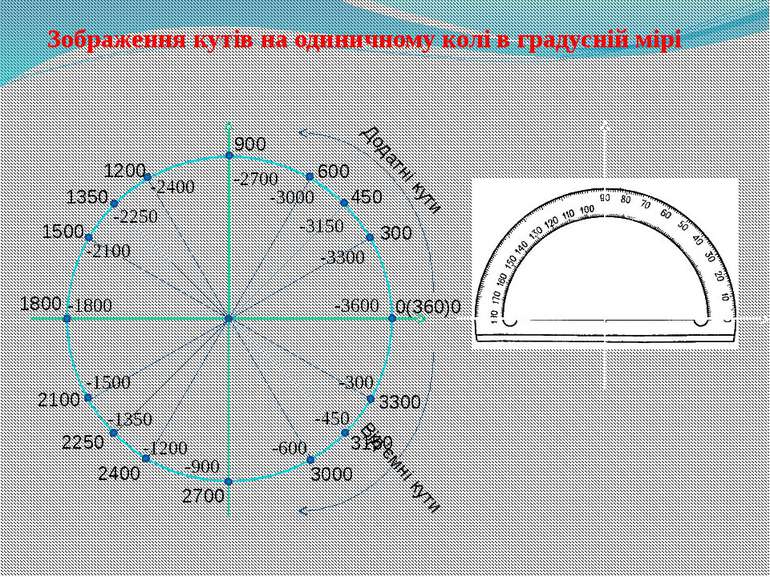
-300 -450 -600 -900 -1200 -1350 -1500 -1800 -2100 -2250 -2400 -2700 -3000 -3150 -3300 -3600 Зображення кутів на одиничному колі в градусній мірі 300 450 600 900 1200 1350 1500 1800 2100 2250 2400 2700 3150 3300 Додатні кути 3000 0(360)0 Від’ємні кути

0 2π Зображення кутів на одиничному колі в радіанах π

Дякуємо за увагу.