Презентація на тему:
Властивості відрізків трапеції та методика їх вивчення в школі

Виконала: Полянська Катерина Ігорівна, студентка 4 курсу напряму підготовки математика Науковий керівник: Працьовитий Микола Вікторович, доктор фізико-математичних наук, професор Властивості відрізків трапеції та методика їх вивчення в школі Тема дипломної роботи:

Мета дослідження – обґрунтування прийомів та засобів підвищення ефективності знань та умінь учнів про властивості відрізків трапеції. Предметом дослідження є процес формування та систематизації знань учнів про властивості відрізків трапеції. Об'єкт дослідження – процес формування знань учнів з планіметрії.

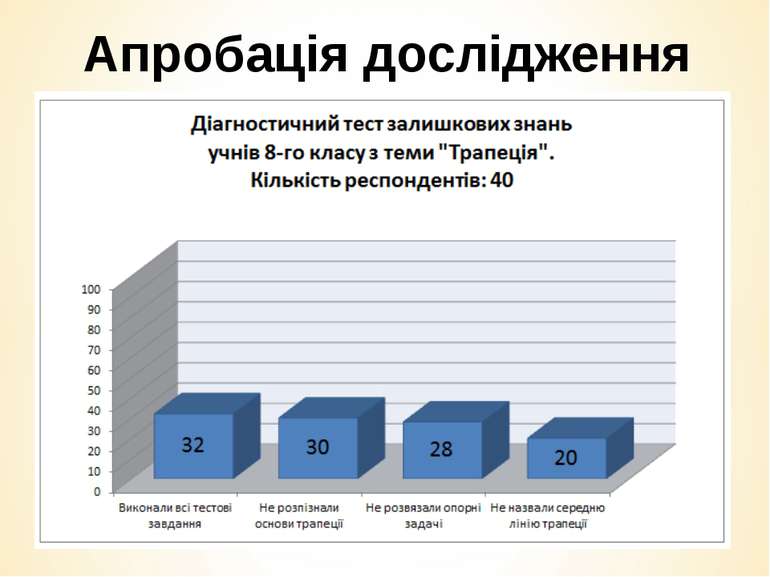
В процесі дослідження нами були сформульовані і розв’язані такі завдання: вивчити психолого-педагогічні основи формування знань учнів про властивості відрізків трапеції; розробити методичні рекомендації, щодо формування знань та умінь учнів з теми «Трапеція»; розглянути прийоми формування знань та вмінь учнів про властивості відрізків трапеції; розглянути можливості використання сучасних засобів навчання на уроках з теми «Трапеція» провести діагностику стану засвоєння знань учнів про властивості відрізків трапеції; провести апробацію результатів дослідження.

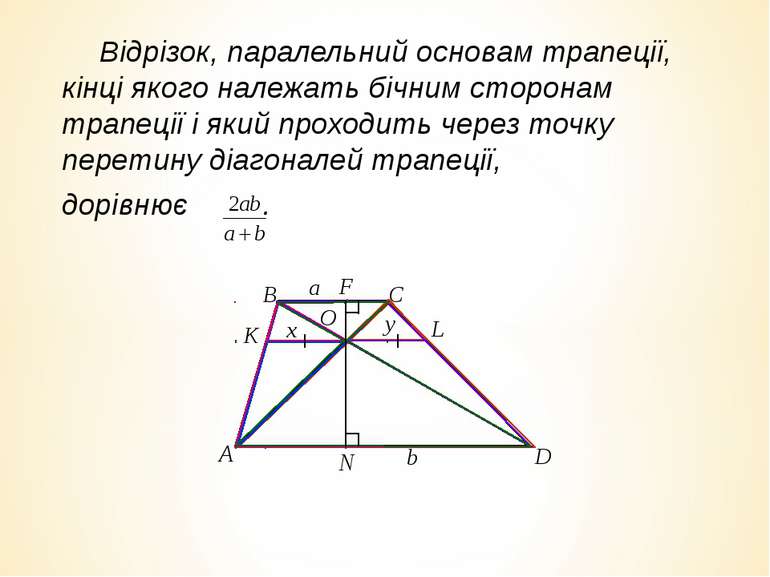
Відрізок, паралельний основам трапеції, який сполучає середини її бічних сторін дорівнює . Відрізок, що з'єднує середини діагоналей трапеції, паралельний її основам і дорівнює . Відрізок, паралельний основам трапеції, кінці якого належать бічним сторонам трапеції і який проходить через точку перетину діагоналей трапеції, дорівнює . Відрізок, паралельний основам трапеції, кінці якого лежать на бічних сторонах ділить трапецію на дві рівновеликі площі і дорівнює . Відрізок, паралельний основам трапеції, кінці якого лежать на бічних сторонах ділить трапецію на дві подібні трапеції і дорівнює , ділить бічну сторону трапеції у відношенні: . Відрізок, паралельний основам трапеції, який проходить через точку перетину продовжених сторін і діагоналей дорівнює . Середня лінія трапеції і відрізок, який з’єднує середини основ, точкою перетину діляться навпіл. Якщо середня лінія трапеції і відрізок, який сполучає середини основ, перпендикулярні, то трапеція рівнобічна. Довжина відрізка прямої, перпендикулярної до бічної сторони, яка проходить через точку перетину діагоналей рівнобічної трапеції з перпендикулярними діагоналями дорівнює , де та довжини основ трапеції. Властивості відрізків трапеції

Відрізок, паралельний основам трапеції, кінці якого належать бічним сторонам трапеції і який проходить через точку перетину діагоналей трапеції, дорівнює .

55. Сума кутів при основах трапеції дорівнює . Довести, що відстань між серединами основ трапеції дорівнює відстані між серединами діагоналей трапеції. Розв’язання 1) Нехай дано трапецію , . Використовуючи властивість відрізка, який проходить через середину діагоналей паралельний основам, маємо: . 2) Продовжимо і , . Оскільки , то . Звідки - прямокутний, де - гіпотенуза, - медіана, проведена до гіпотенузи. За властивістю . 3) Розглянемо - прямокутний . - гіпотенуза, - медіана до гіпотенузи, 4) . Отже, . Відповідь:

Апробація дослідження

1. Полянська К. І. Систематизація знань учнів з планіметрії при розв’язуванні задач на обчислення площі паралелограма / К.І. Полянська // Задача одна – способи розв’язання різні. Вип. 1. - Вінниця: Вид-во В. : ВДПУ імені Михайла Коцюбинського. – 2011. – С. 140-143. 2. Полянська К.І. Інформаційно-комунікаційні технології навчання у роботі з учнями з вадами розвитку / К.І. Полянська // Інформаційно-комунікаційні технології методичної підготовки вчителів – Кривий Ріг, 2011 р.- С. 90-92. 3. Полянська К.І. Типові проблеми реалізації профільного навчання в старшій школі / К.І. Полянська // Всеукраїнської науково-методичної конференції «Профільне навчання: проблеми, перспективи, шляхи реалізації» – Черкаси - 2011. – С. 245-248. 4. Полянська К.І. Введення поняття трапеції в шкільному курсі планіметрії / К.І. Полянська // Технології введення математичних понять у процесі навчання математики. Вип. 2. - Вінниця: Вид-во В. : ВДПУ імені Михайла Коцюбинського. – 2012. – С. 184-189. 5. Полянська К.І. Використання інтерактивної дошки у процесі підготовки майбутніх фахівців / К.І. Полянська // Всеукраїнська конференція студентських наукових робіт в галузі професійної освіти. “ Теорія та методика розробки та використання засобів навчання ”– Харків – 2012. 6. Полянська К.І. Використання інтерактивної дошки у процесі підготовки майбутніх фахівців / Тези Міжнародної науково-практичної конференції “Проблеми та перспективи фахової підготовки вчителя математики” (26-27 квітня 2012р., Вінниця). – В. : ВДПУ імені Михайла Коцюбинського, 2012. – С. 70-72.

Дякую за увагу!!!