Презентація на тему:
ЦІЛІ ВИРАЗИ

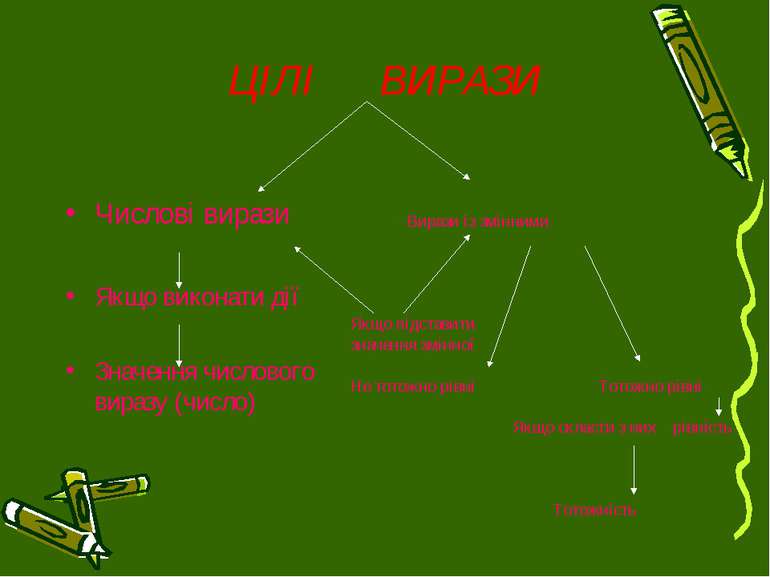
ЦІЛІ ВИРАЗИ Числові вирази Якщо виконати дії Значення числового виразу (число) Вирази із змінними Якщо підставити значення змінної Не тотожно рівні Тотожно рівні Якщо скласти з них рівність Тотожність

Це цікаво знати Алгебра як наука складалася завдяки зусиллям багатьох людей протягом багатьох років. Алгебраїчні знаки, умовні позначення та правила дій вводилися поступово різними вченими і в різних країнах. Узбецький учений ХУ ст. ал-Каші “а4” називав “квадрато-квадрат”, “а5” – “квадрато-куб”, “а6” – “кубо-куб” і т. д. Л. Ф. Магницький степінь “а3” записував “куб” або “кубик”. Символи а2, а3, а4 і т. д. вперше зустрічаються у французького вченого Рене Декарта в 1637 р. Повна теорія степенів була створена європейськими вченими тільки в ХУІІ ст.

СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ am . an = am+n (m ϵ N, n ϵ N), x10 . x6 . x = x17 am : an = am-n, (a ≠ 0, m ϵ n) p12 : p7 = p5 (am)n = amn, (m ϵ N, n ϵ N), (x3)10 = x30 (ab)n = an . bn, (n ϵ N) (2x2y4)3 = 8x6y12

ОДНОЧЛЕНИ – у4, х.х.х, 9, с, 5р8 АЛГОРИТМ 1 Множення одночленів Знайдіть добуток коефіцієнтів. Показники степенів однакових змінних додайте. Якщо змінна входить лише в один з співмножників, то допишіть її у добуток. 0,5ху2 . 0,2х2у = 0,5.0,2х1+2 . у2+1 = 0,1х3у3 АЛГОРИТМ 2 Піднесення одночленів до степеня Піднесіть до степеня коефіцієнт одночлена. Показник степеня кожної змінної одночлена помножте на показник степеня, до якого підноситься одночлен. (-2х2у)3 = (-2)3 . (х2)3 . (у1)3 = -8х6у3

Многочлен Многочленом називається сума кількох одночленів. Одночлени, які складають многочлен, називаються його членами. Подібні доданки многочлена називають подібними членами многочлена. Многочлен, що є сумою одночленів стандартного вигляду, серед яких немає подібних членів, називається многочленом стандартного вигляду. Степенем многочлена стандартного вигляду називається степінь одночлена, який є найбільшим серед степенів одночленів, що утворюють даний многочлен. Кожний многочлен є цілим виразом. Додавання та віднімання многочленів виконують за правилами розкриття дужок та зведення подібних доданків.

Множення одночлена на многочлен Щоб помножити одночлен на многочлен, треба одночлен помножити на кожний член многочлена й одержані добутки додати. Тобто множення одночлена на многочлен здійснюється на основі розподільної властивості множення. 5x(3x – 2) = 15x2 - 10x.

Множення многочлена на многочлен Щоб помножити многочлен на многочлен, досить кожний член одного многочлена помножити на кожний член другого многочлена й одержані добутки додати. (7m + 3)(2m – 1) = 14m2 - 7m + 6m – = = 14m2 – m -3.