Презентація на тему:
Геометричний зміст похідної

Геометричний зміст похідної

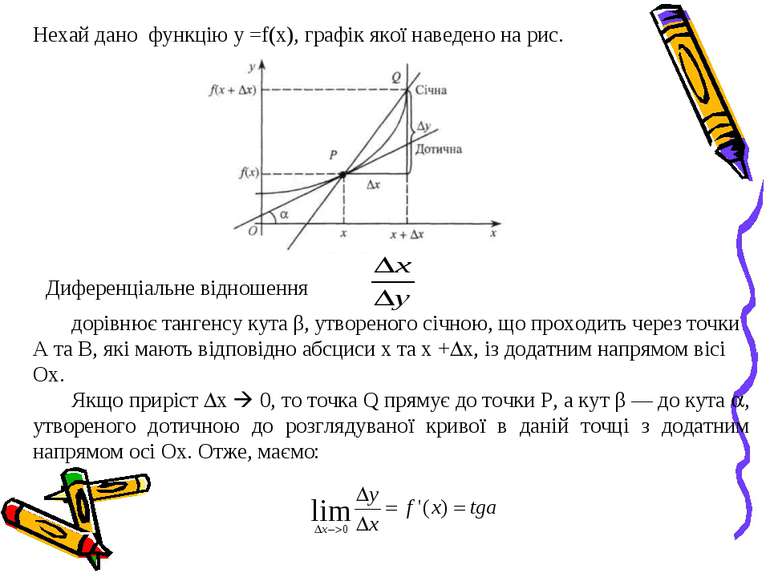
Нехай дано функцію у =f(x), графік якої наведено на рис. Диференціальне відношення дорівнює тангенсу кута β, утвореного січною, що проходить через точки А та В, які мають відповідно абсциси х та х + x, із додатним напрямом вісі Ох. Якщо приріст х 0, то точка Q прямує до точки P, а кут β — до кута , утвореного дотичною до розглядуваної кривої в даній точці з додатним напрямом осі Ох. Отже, маємо:

Геометричний зміст похідної Значення похідної в деякій точці дорівнює тангенсу кута, утвореного дотичною до кривої в цій точці з додатним напрямом осі Ох.

Рівняння дотичної до графіка функції Розглянемо функцію у = f(x). її графік зображено на рис. У точці М(х0, у0) проведено дотичну до кривої у = f(x). Складемо рівняння дотичної AM, знаючи координати точки М(х0; у0) дотику і рівняння у = f(x) кривої. Дотична — це пряма. Рівняння будь-якої прямої має вигляд: у = kx + b. Оскільки k = f'(x0), тому рівняння дотичної має вигляд: Знайдемо b, виходячи з того, що дотична проходить через точку М(х0; у0) і тому її координати задовольняють рівнянню дотичної: y0=f `(x0) • x0+b, звідси b = у0- f'(x0) • х0. Тепер підставимо значення b в рівняння дотичної і одержимо: Отже, рівняння дотичної до кривої у = f(x) в точці М(х0;у0) має вигляд:

Рівняння дотичної до графіка функції Рівняння дотичної до кривої у = f(x) у заданій точці х0 можна знаходити за таким планом (схемою): 1. Записуємо рівняння дотичної: 2. Знаходимо у0 = f(x0). 3. Знаходимо значення f'(x) у точці x0: f'(x0). 4. Підставляємо значення х0, у0 і f'(x0) у рівняння