Презентація на тему:
Похідна. Фізичний і геометричний зміст похідної.

Похідна. Фізичний і геометричний зміст похідної.

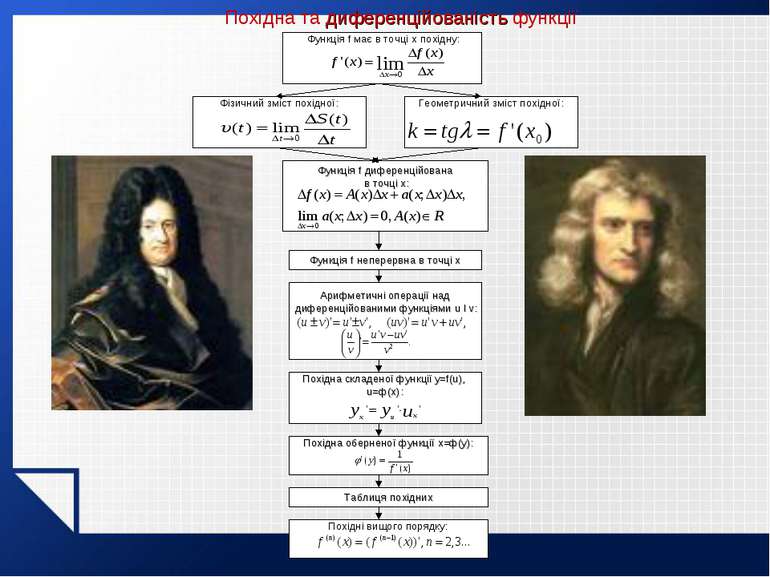
Похідна та диференційованість функції Функція f має в точці x похідну: Фізичний зміст похідної: Геометричний зміст похідної: Функція f диференційована в точці x: Функція f неперервна в точці x Арифметичні операції над диференційованими функціями u I v: Похідна складеної функції y=f(u), u=ф(x): Похідна оберненої функції x=ф(y): Таблиця похідних Похідні вищого порядку:

І.Ньютон сформулював дві основні проблеми математичного аналізу: 1). Довжина шляху, який долається, є постійною(тобто в будь-який момент часу); необхідно знайти швидкість руху у пропонований час; 2). Швидкість руху постійно дана; необхідно знайти довжину пройденого у запропонований час шляху.

1). Задача про миттєву швидкість: 2). Задача про знаходження змінного струму, який проходить по провіднику:

3). Друга похідна: (t)

4). Приклад:

Висновок:

під редакцією М.І.Сканаві.

Тіло масою m0 рухається прямолінійно за законом S(t)= αt2 +βt+ λ α, β, λ –сталі Довести, що сила яка діє на тіло стала Задача 15.120.

Доведення: F=m0a a(t)=V’(t)=S”(t); S’(t)=(αt2+ βt+ λ)’=2αt+β; a(t)=S”(t)=(2αt+ β)’=2α; a(t)=2α, α=const;

Сила, що діє на тіло – стала.

Задача 15.121 Тіло масою m0 рухається прямолінійно за законом Довести, що сила, яка діє на тіло, пропорційна кубу пройденого шляху.

Доведення F=m0a;

Сила, що діє на тіло, пропорційна кубу пройденого шляху.

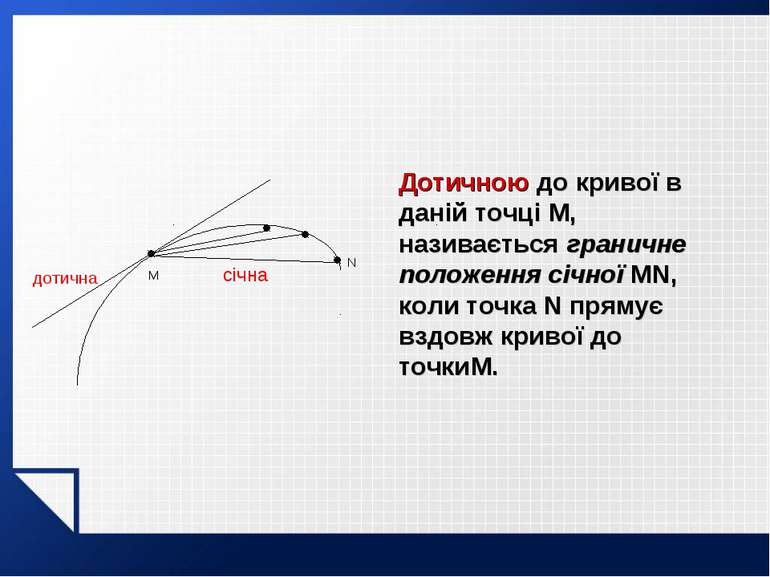
N дотична січна M Дотичною до кривої в даній точці M, називається граничне положення січної MN, коли точка N прямує вздовж кривої до точкиM.

y x k-кутовий коефіцієнт рівняння дотичної до графіка функції в точці з абсцисою .

геометричного змісту похідної

1) Обчисліть , якщо кут між дотичною проведеної до графіка функції у точці з абсцисою і додатнім напрямом осі OX, дорівнює . Розв’язання

2) До графіка функції проведено дотичну у точці з абсцисою . Обчисліть тангенс кута нахилу дотичної до додатнього напрямку осі абсциса. Розв’язання

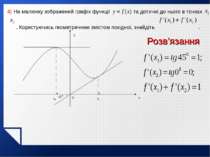
3) На малюнку зображено графік функції і дотичну до нього в точці з абсцисою . y x 1 1 Розв’язання Знайти значення

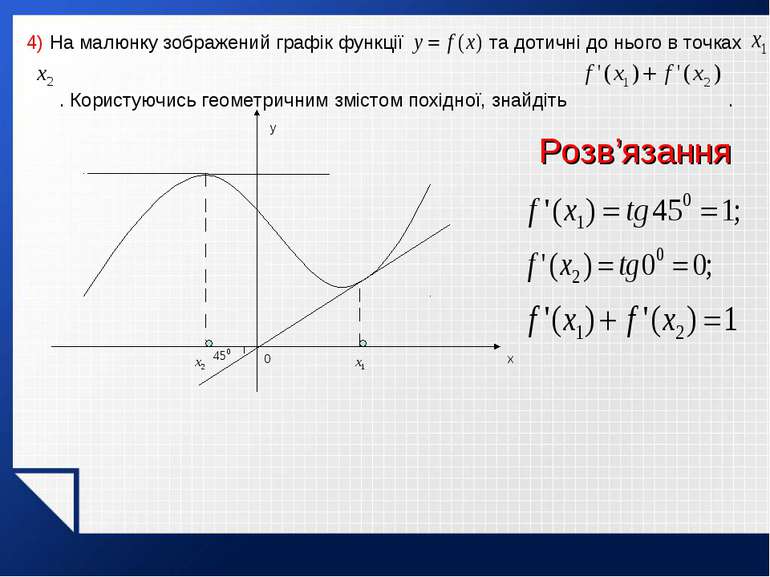
4) На малюнку зображений графік функції та дотичні до нього в точках . Користуючись геометричним змістом похідної, знайдіть . y x 0 Розв’язання

5) Знайдіть, при яких значеннях параметра а дотична до графіка функції у точці з абсцисою проходить через точку N(3;4). Розв’язання

y1=k1x +b1, k1=k2, y1IIy2 y2=k2x +b2,

y1=k1x +b1, k1·k2= -1, y1 I y2 y2=k2x +b2,

Задача 1 На параболі y= 4- X вибрано дві точки з абсцисами x= -1 і x=3. Через ці точки проведено січну. Знайти рівняння дотичної до параболи, яка паралельна січній.

Розв'язання 1) y = kx + b – рівняння січної Дана січна проходить через точки : (-1;3), (3;-5) Складаємо рівняння січної: 3 = -k + b; 8= -4k, -5 =3k + b; k= -2, то b=1 y= -2x +1 – рівняння січної

2)y=f(x0) + f '(x0)(x-x0) – рівняння дотичної f(x0)=4 - x02; f '(x0)= -2x0; y =4- x02 - 2x0(x-x0), y = -2x0x +x02 + 4,

3) y1=kx +b1, y2=k2x +b2, k1=k2 y1||y2 4)За умовою паралельності прямих, маємо : -2x0= -2 x0=1. Отже, y = -2x-3 - шукане рівняння дотичної.

Записати рівняння дотичної до графіка функції f(x)= -x2+4, яка перпендикулярна до прямої x-2y+2=0. Задача 2

Розв'язання y = f(x0) +f '(x0)(x-x0), f (x0) = -x02+4, f '(x0) = -2x0, y= -x02 +4 - 2x0(x-x0), y= -2x0x +x02 +4 - рівняння дотичної y= 0,5x +1 - рівняння прямої перпендикулярної до дотичної

y1=k1x +b1 і y2=k2 +b2 k1· k2= -1y1 I y2

За умовою перпендикулярності прямих маємо : якщо k1= -2x0, k2=0,5,то -2x0·0,5= -1,x0=1. Отже, y= -2x+5 - шукане рівняння дотичної

Задача 3 Знайти величину кута між двома дотичними проведеними з точки (0;-1) до графіка функції y=x2.

Задача 4 Знайти площу трикутника, утвореного бісектрисами координатних кутів і дотичної до кривої y= в точці М(3;2)