Презентація на тему:
Гра “Геометричний хокей”

Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя. Піфагор

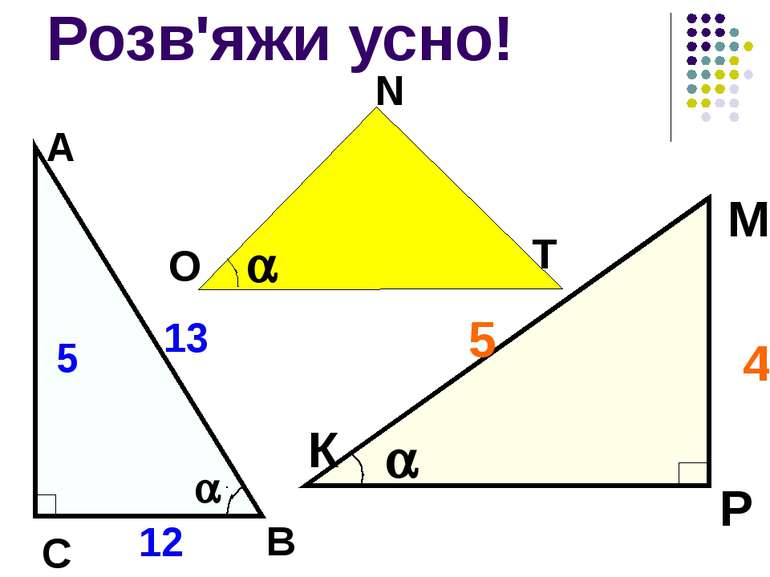
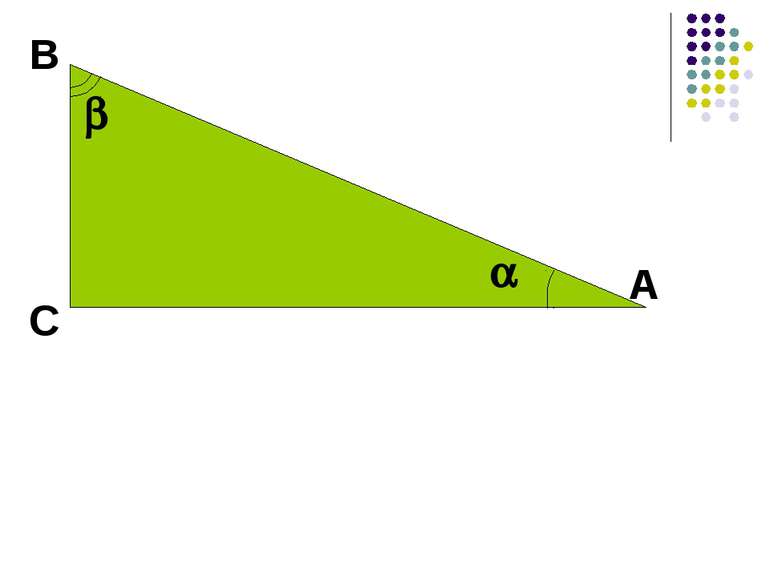
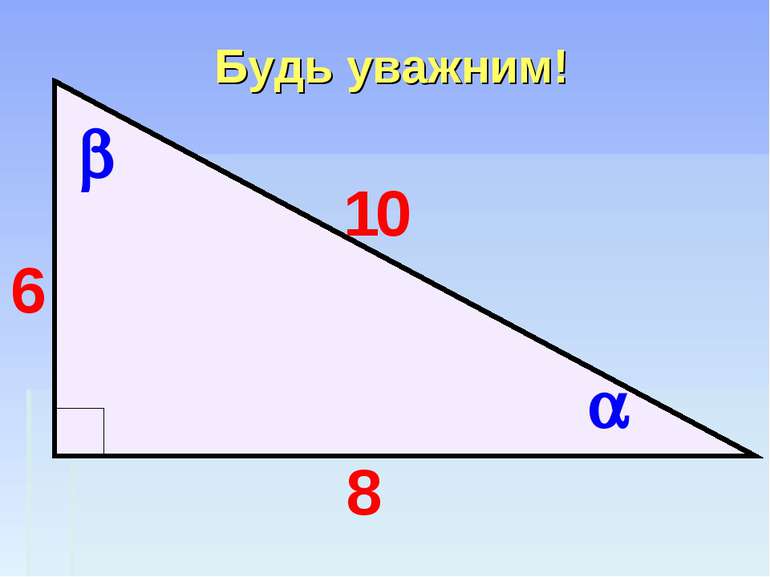
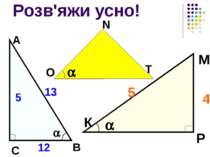
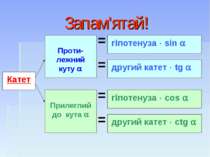
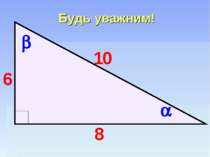
Гра “Геометричний хокей” 1. Як називаються сторони прямокутного трикутника? 2. Що таке косинус гострого кута прямокутного трикутника? Від чого залежить значення косинуса кута? Сформулюйте теорему Піфагора. 5. Які наслідки має ця теорема? 6. Чому дорівнює гіпотенуза прямокутного трикутника зі сторонами 3 дюйма та 4 дюйма? Як називається такий трикутник? 7. Який трикутник називається рівнобедреним? Які властивості він має? 6 6 5 4 3 2 1 5 4 3 2 1

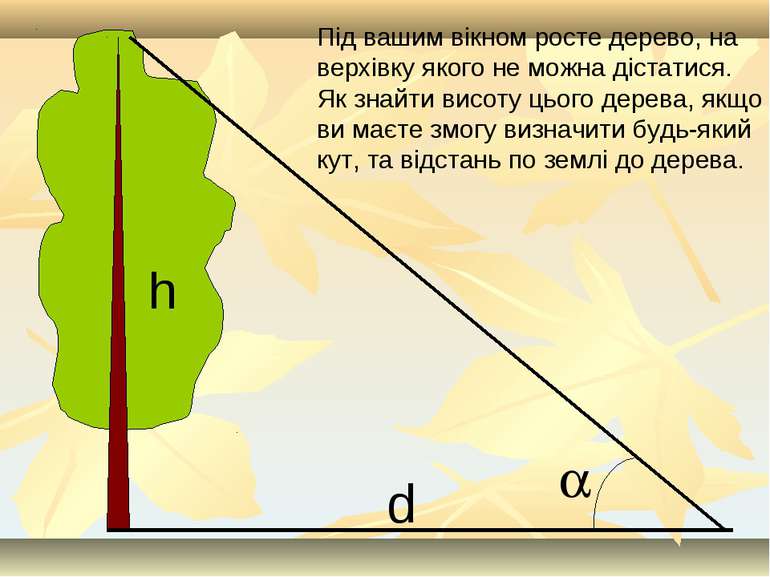
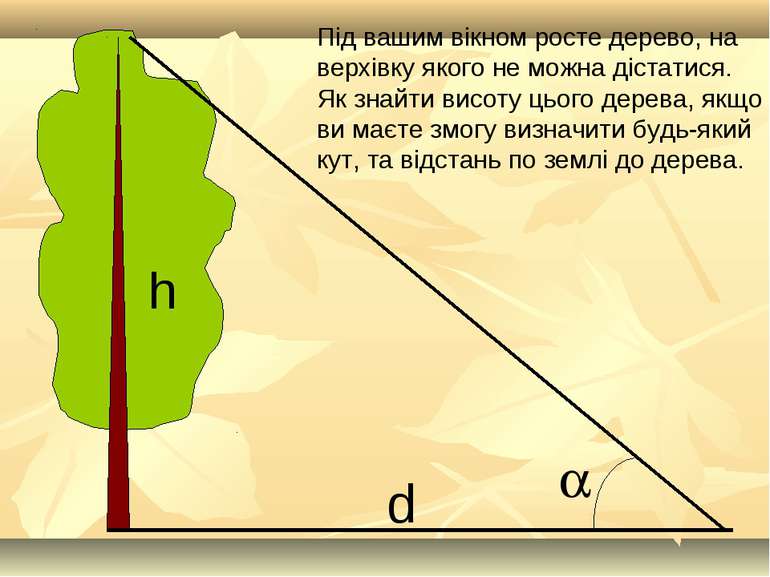
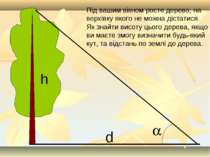
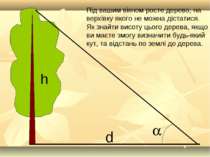
Під вашим вікном росте дерево, на верхівку якого не можна дістатися. Як знайти висоту цього дерева, якщо ви маєте змогу визначити будь-який кут, та відстань по землі до дерева.

Бережіть природу!

Співвідношення кутів та сторін у прямокутному трикутнику Тема уроку Добре засвоєна мудрість не забувається ніколи Піфагор

Запам'ятай!

А В О

Розв'яжи усно! 12 13 В Н О Т N

С А В

Запам'ятай!

Запам'ятай!

Під вашим вікном росте дерево, на верхівку якого не можна дістатися. Як знайти висоту цього дерева, якщо ви маєте змогу визначити будь-який кут, та відстань по землі до дерева.

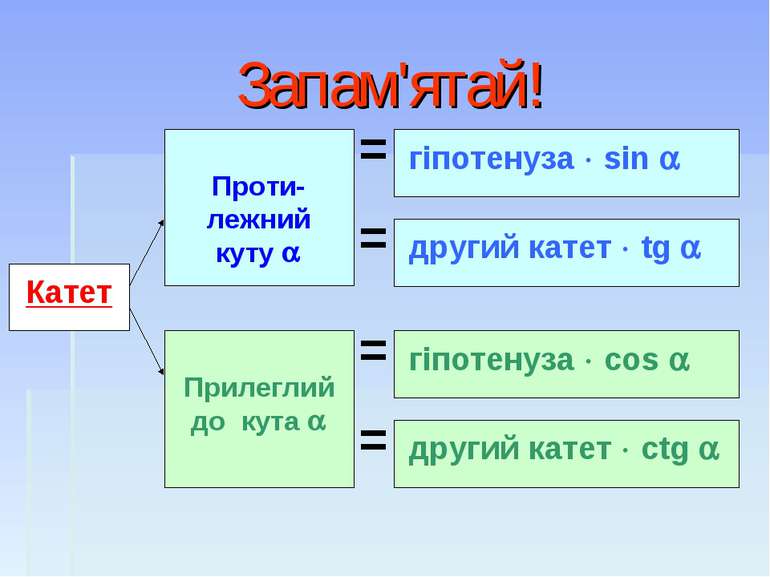
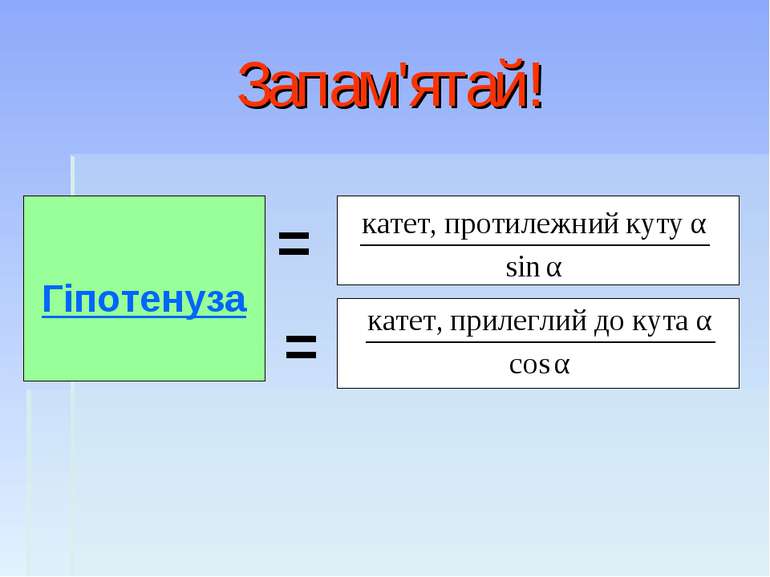
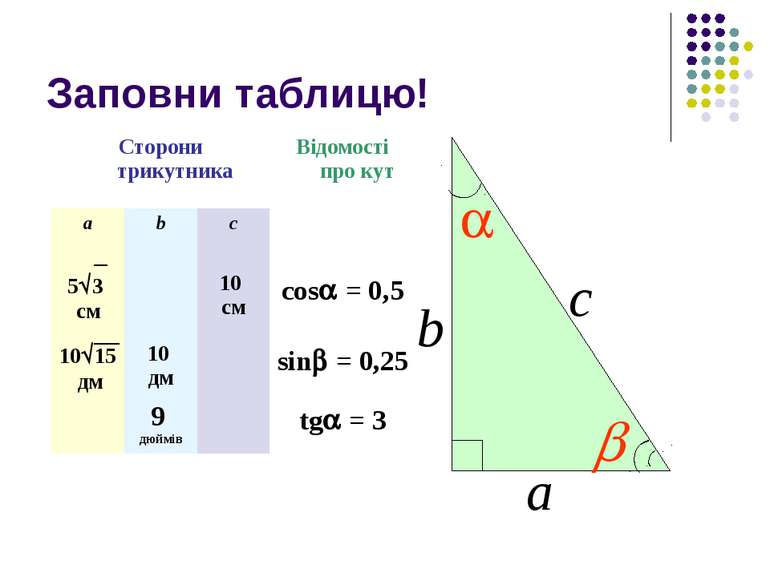
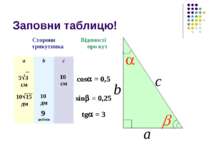
Заповни таблицю! b а с Сторони трикутника Відомості про кут а b с 5 3 см 10 см cos = 0,5 10 15 дм 10 дм sin = 0,25 9 дюймів tg = 3

І рівень Сторони трикутника Відомості про кут а b с 5 3 см 5 см 10 см cos = 0,5 10 15 дм 10 дм 40 дм sin = 0,25 27 дюймів 9 дюймів 9 10 дюймів tg = 3

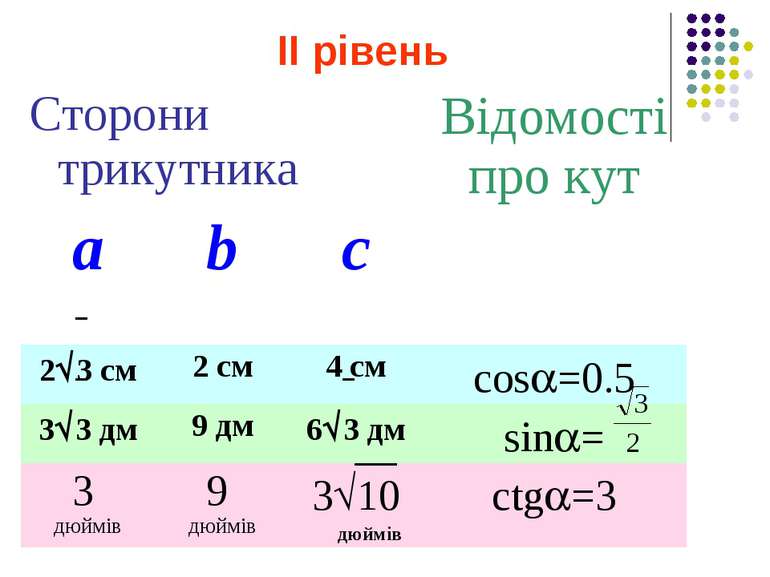
ІІ рівень Сторони трикутника Відомості про кут а b с 2 3 см 2 см 4 см cos =0.5 3 3 дм 9 дм 6 3 дм sin = 3 дюймів 9 дюймів 3 10 дюймів сtg =3

Гіпарх із Нікеї (ІІ ст. до н.е.) Брадіс В.М. (1890-1975)

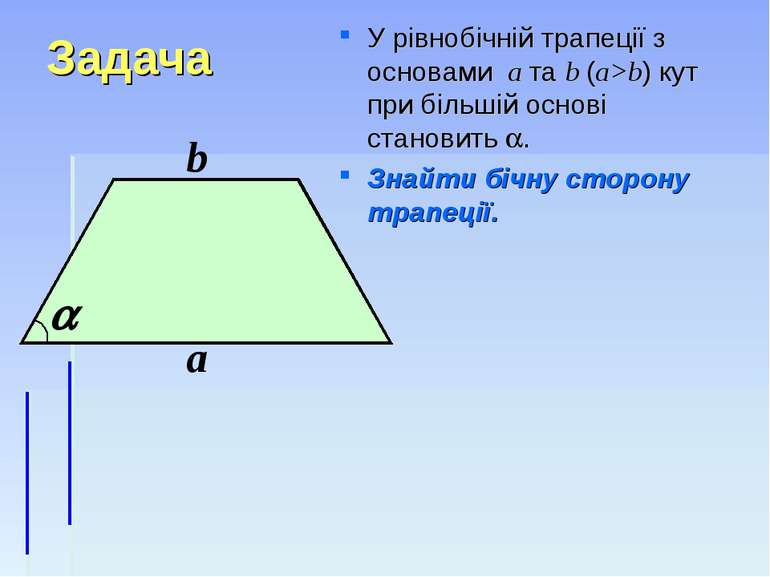
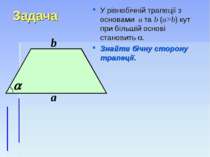
Задача У рівнобічній трапеції з основами а та b (а>b) кут при більшій основі становить . Знайти бічну сторону трапеції. а b

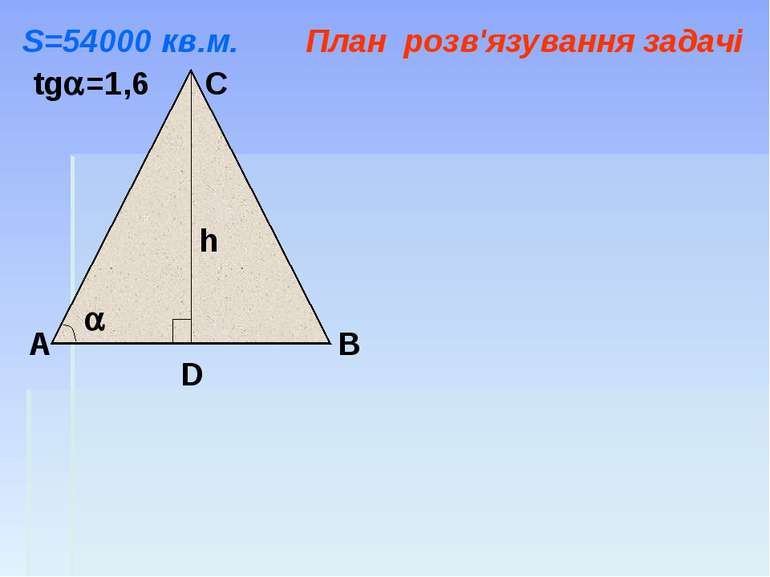
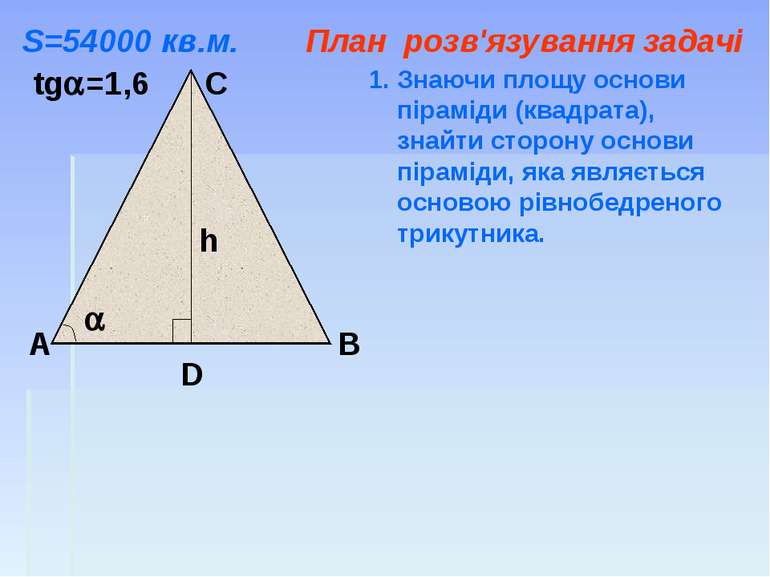
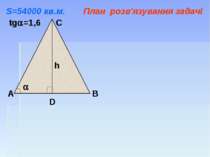
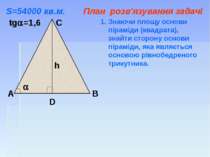
Найбільшою серед єгипетських пірамід є піраміда Хеопса. Площа її основи близько 54 000 кв.м. Кожен, хто приїздить подивитись на них, мріє піднятися на вершину піраміди. Бічна грань піраміди – рівнобедрений трикутник, тангенс кута при основі якого дорівнює 1,6. За скільки часу турист підніметься на вершину піраміди Хеопса, якщо він рухатиметься зі швидкістю 0,5 км/год.

А В С D tg =1,6 h S=54000 кв.м. План розв'язування задачі

А В С D tg =1,6 h Знаючи площу основи піраміди (квадрата), знайти сторону основи піраміди, яка являється основою рівнобедреного трикутника. S=54000 кв.м. План розв'язування задачі

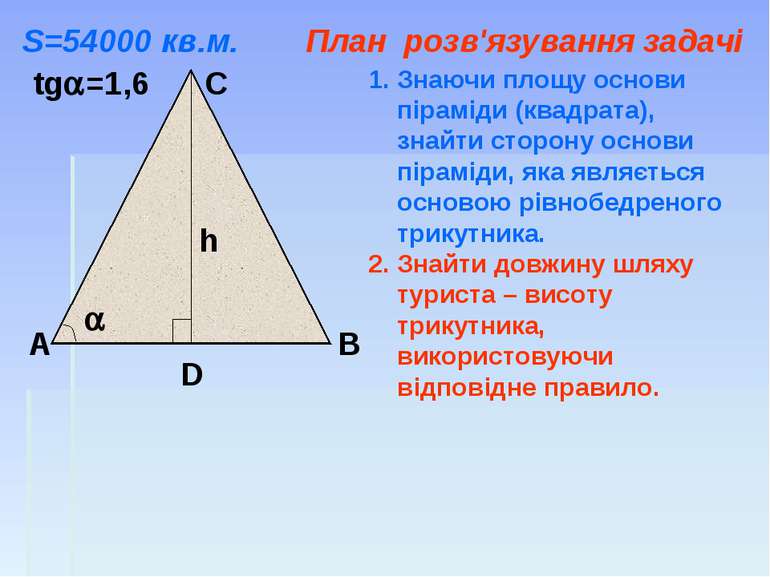
А В С D tg =1,6 h Знаючи площу основи піраміди (квадрата), знайти сторону основи піраміди, яка являється основою рівнобедреного трикутника. Знайти довжину шляху туриста – висоту трикутника, використовуючи відповідне правило. S=54000 кв.м. План розв'язування задачі

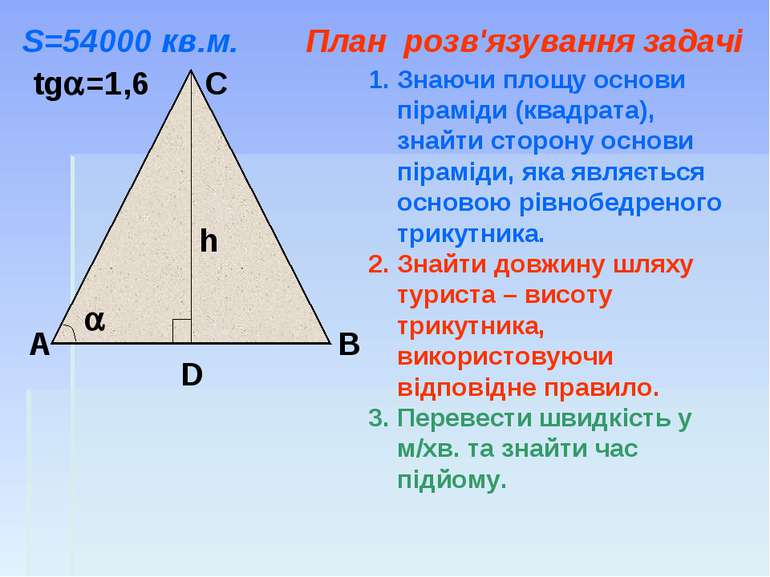
А В С D tg =1,6 h Знаючи площу основи піраміди (квадрата), знайти сторону основи піраміди, яка являється основою рівнобедреного трикутника. Знайти довжину шляху туриста – висоту трикутника, використовуючи відповідне правило. Перевести швидкість у м/хв. та знайти час підйому. S=54000 кв.м. План розв'язування задачі

Будь уважним!

Домашнє завдання Опрацювати п. 67, Вивчити правила знаходження сторін прямокутного трикутника Розв’язати задачу, запропоновану сусідом. Розв’язати № 44, 45, 47. Принести на урок «Чотиризначну таблицю» Брадіса або калькулятор, що має можливість обраховувати тригонометричні функції кутів.