Презентація на тему:
Застосування похідної до дослідження функції

Творча робота з вищої математики на тему: Застосування похідної до дослідження функції Виконали:студентки 1 курсу,7 групи Литвин Тетяна і Шкаруба Тетяна.

Похідна Похідна  — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною. Графік функції, що позначено чорним кольором, та дотична до нього (червоний колір). Значення нахилу дотичної є значенням похідної у вказаній точці.

Застосування похідної до дослідження динаміки функції. Загальне дослідження функції та побудову їх графіків зручно використовувати за наступною схемою: 1. Елементарні дослідження: знайти область визначення функції; точки перетину з осями координат; перевірити функцію на парність. 2. Знайти точки розриву функції та її односторонні границі 3. Знаходження похилих асимптот. 4. Знайти точки екстремуму та інтервали зростання та спадання функції. 5. Побудувати графік функції, враховуючи всі одержані результати дослідження

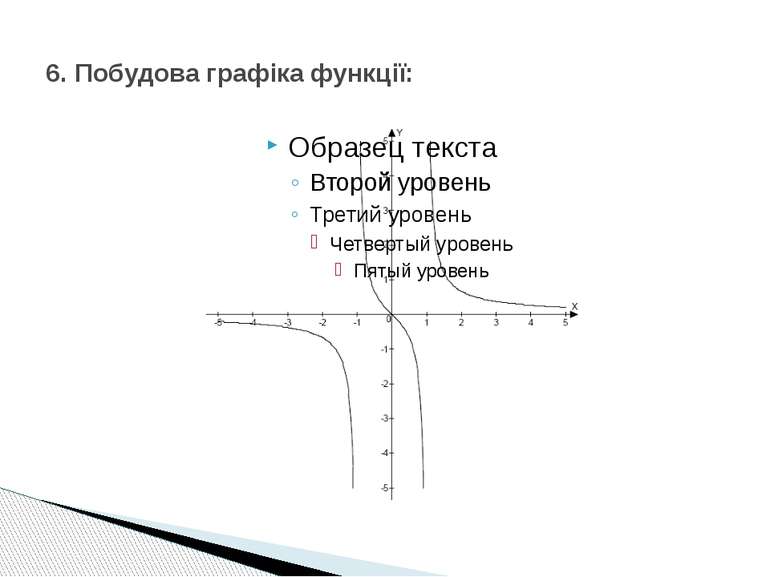
П р и к л а д: Дослідити функцію і побудувати її графік: Розв’язання: 1. Елементарні дослідження: Область визначення функції : Точки перетину графіка функції з осями координат: (0;0) − єдина точка перетину з віссю абсцис та ординат. Функція непарна, так як: Отже графік функції симетричний відносно початку координат.

2. Дослідження точок розриву: Отже, х =-1 і х =1 − вертикальні асимптоти.

3. Знаходження похилих асимптот: Похилі асимптоти визначатимемо за формулою: у =kх +b . Для цього знайдемо невідомі коефіцієнти k і b: Тоді рівняння асимптоти набуватиме вигляду: у = 0.

Прирівняємо першу похідну до нуля: Так як рівняння не має розв’язків, то критичних точок першого роду не має. Тому на числовій осі 0Х позначаємо лише точки розриву функції: Отже, функція спадає на всій області визначення. 4. Дослідження функції на монотонність: Знайдемо першу похідну функції:

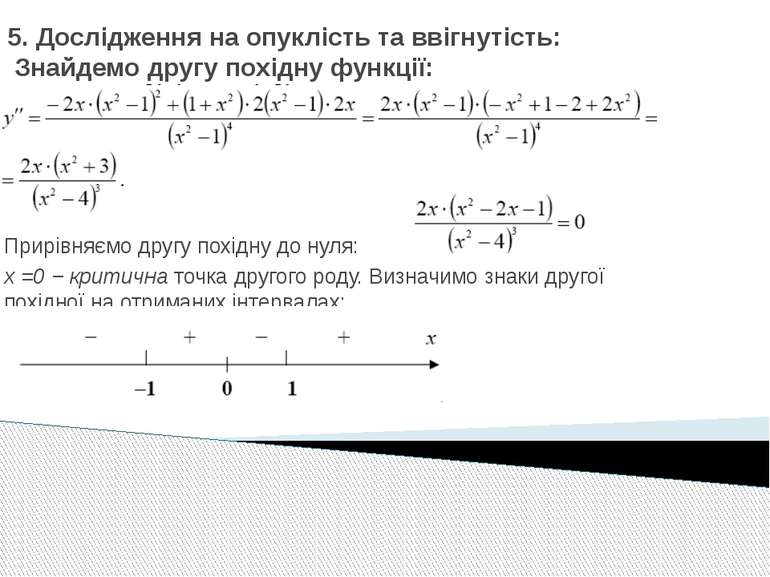
5. Дослідження на опуклість та ввігнутість: Знайдемо другу похідну функції: Прирівняємо другу похідну до нуля: х =0 − критична точка другого роду. Визначимо знаки другої похідної на отриманих інтервалах:

Отже, функція опукла вниз на проміжках: опукла вгору − Точка (0; 0) – точка перегину.

6. Побудова графіка функції: