Презентація на тему:
СТАТИСТИЧНА ПЕРЕВІРКА ГІПОТЕЗ
Завантажити презентацію
СТАТИСТИЧНА ПЕРЕВІРКА ГІПОТЕЗ
Завантажити презентаціюПрезентація по слайдам:
ПЛАН Параметричні і непараметричні статистичні гіпотези Нульова й альтернативна гіпотези Прості і складні статистичні гіпотези Область прийняття гіпотези. Критична область. Критична точка Алгоритм перевірки нульової гіпотези Помилки першого та другого роду. Потужність критерію Перевірка правильності нульової гіпотези про значення генеральної середньої Перевірка правильності нульової гіпотези про рівність двох генеральних середніх (M(X) = M(Y)) Малий обсяг вибірки i невідомі значення дисперсій генеральної сукупності Критерій узгодженості Пірсона.
Інформація, яку дістають на підставі вибірки, реалізованої із генеральної сукупності, може бути використана для формулювання певних суджень про всю генеральну сукупність. Наприклад, розпочавши виготовляння препарату нового типу від алергії, відбирають певну кількість цього препарату і піддають його певним тестам. За результатами тестів можна зробити висновок про те, чи кращий новий препарат від препарату старого типу, чи ні. А це, у свою чергу, дає підставу для прийняття рішення: виготовляти їх чи ні. Такі рішення називають статистичними.
Статистичні рішення мають ймовірнісний характер, тобто завжди існує ймовірність того, що прийняті рішення будуть помилковими. Головна цінність прийняття статистичних рішень полягає в тому, що в межах ймовірнісних категорій можна об’єктивно виміряти ступінь ризику, що відповідає тому чи іншому рішенню. Будь-які статистичні висновки, здобуті на підставі обробки вибірки, називають статистичними гіпотезами.
Параметричні і непараметричні статистичні гіпотези Статистичні гіпотези про значення параметрів ознак генеральної сукупності називають параметричними. Наприклад, висувається статистична гіпотеза про числові значення генеральної середньої , генеральної дисперсії Dг, генерального середнього квадратичного відхилення г та ін. Статистичні гіпотези, що висуваються на підставі обробки вибірки про закон розподілу ознаки генеральної сукупності, називаються непараметричними. Так, наприклад, на підставі обробки вибірки може бути висунута гіпотеза, що ознака генеральної сукупності має нормальний закон розподілу, експоненціальний закон та ін.
Нульова й альтернативна гіпотези Гіпотезу, що підлягає перевірці, називають основною. Оскільки ця гіпотеза припускає відсутність систематичних розбіжностей (нульові розбіжності) між невідомим параметром генеральної сукупності і величиною, що одержана внаслідок обробки вибірки, то її називають нульовою гіпотезою і позначають Н0. Зміст нульової гіпотези записується так:
Нульова й альтернативна гіпотези Кожній нульовій гіпотезі можна протиставити кілька альтернативних (конкуруючих) гіпотез, які позначають символом Н , що заперечують твердження нульової. Так, наприклад, нульова гіпотеза стверджує: , а альтернативна гіпотеза — , тобто заперечує твердження нульової.
Прості і складні статистичні гіпотези Проста гіпотеза, як правило, належить до параметра ознак генеральної сукупності і є однозначною. Наприклад, згідно з простою гіпотезою параметр генеральної сукупності дорівнює конкретному числу, а саме:
Прості і складні статистичні гіпотези Складна статистична гіпотеза є неоднозначною. Вона може стверджувати, що значення параметра генеральної сукупності належить певній області ймовірних значень, яка може бути дискретною і неперервною. Наприклад:
Область прийняття гіпотези. Критична область. Критична точка Множину всіх можливих значень статистичного критерію K можна поділити на дві підмножини А і , які не перетинаються. Сукупність значень статистичного критерію K А, за яких нульова гіпотеза не відхиляється, називають областю прийняття нульової гіпотези.
Область прийняття гіпотези. Критична область. Критична точка Сукупність значень статистичного критерію K , за яких нульова гіпотеза не приймається, називають критичною областю. Точку або кілька точок, що поділяють множину на підмножини А і , називають критичними і позначають через Kкр. Існують три види критичних областей:
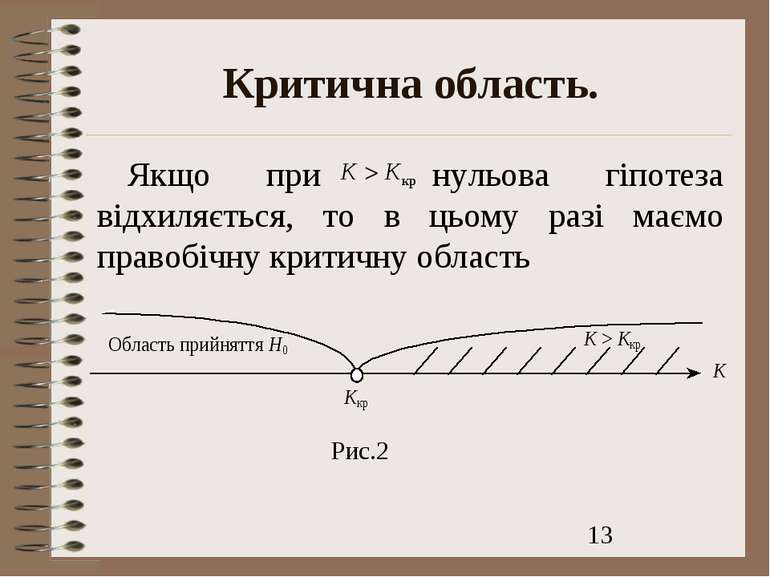
Критична область. Якщо при нульова гіпотеза відхиляється, то в цьому разі маємо правобічну критичну область Рис.2
Критична область. Якщо ж при і при нульова гіпотеза відхиляється, то маємо двобічну критичну область Рис.3
Алгоритм перевірки нульової гіпотези Для перевірки правильності Н0 задається так званий рівень значущості . — це мала ймовірність, якою наперед задаються. Вона може набувати значення = 0,005; 0,01; 0,001. В основу перевірки Н0 покладено принцип, тобто ймовірність того, що статистичний критерій потрапляє в критичну область , дорівнює малій ймовірності . Якщо ж виявиться, що а ця подія малоймовірна і все ж відбулася, то немає підстав приймати нульову гіпотезу.
Алгоритм перевірки нульової гіпотези Пропонується такий алгоритм перевірки правильності Н0: 1. Сформулювати Н0 й одночасно альтернативну гіпотезу Н . 2. Вибрати статистичний критерій, який відповідав би сформульованій нульовій гіпотезі. 3. Залежно від змісту нульової та альтернативної гіпотез будується правобічна, лівобічна або двобічна критична область, а саме: нехай , тоді, якщо
Алгоритм перевірки нульової гіпотези , то вибирається правобічна критична область, якщо , то вибирається лівобічна критична область і коли , то вибирається двобічна критична область. 4. Для побудови критичної області (лівобічної, правобічної чи двобічної) необхідно знайти критичні точки. За вибраним статистичним критерієм та рівнем значущості знаходяться критичні точки. 5. За результатами вибірки обчислюється спостережуване значення критерію .
Помилки першого та другого роду. Потужність критерію Якою б не була малою величина , потрапляння спостережуваного значення у критичну область ніколи не буде подією абсолютно неможливою. Тому не виключається той випадок, коли Н0 буде правильною, а , а тому нульову гіпотезу буде відхилено. Отже, при перевірці правильності Н0 можуть бути допущені помилки. Розрізняють при цьому помилки першого і другого роду. Якщо Н0 є правильною, але її відхиляють на основі її перевірки, то буде допущена помилка першого роду. Якщо Н0 є неправильною, але її приймають, то в цьому разі буде допущена помилка другого роду.
Помилки першого та другого роду. Потужність критерію Між помилками першого і другого роду існує тісний зв’язок. Нехай, для прикладу, перевіряється . При великих обсягах вибірки n , як випадкова величина, закон розподілу ймовірностей якої асимптотично наближатиметься до нормального з числовими характеристиками:
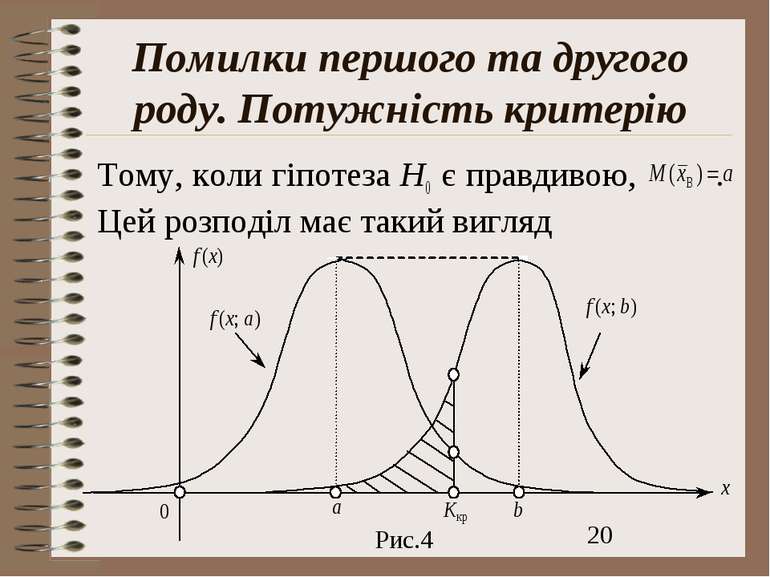
Помилки першого та другого роду. Потужність критерію Тому, коли гіпотеза Н0 є правдивою, . Цей розподіл має такий вигляд Рис.4
Помилки першого та другого роду. Потужність критерію Коли альтернативна гіпотеза заперечує Н0 і стверджує , то в цьому разі нормальна крива буде зміщена праворуч (на рис. 4, крива f (x; b)). Коли , то Н0 відхиляється з ймовірністю помилки першого роду:
Помилки першого та другого роду. Потужність критерію Коли , то Н0 не відхиляється, хоча може бути правильною альтернативна гіпотеза Н . Отже, в цьому разі припускаються помилки другого роду. Ймовірність цієї помилки, яку позначають символом , може бути визначена на кривій f (x; b), а саме:
Помилки першого та другого роду. Потужність критерію Ця ймовірність на рис. 4 показана штрихуванням площі під кривою f (x; b), що міститься ліворуч Kкр. Якщо з метою зменшення ризику відхилити правильну гіпотезу Н0 зменшуватимемо значення , то в цьому разі критична точка Kкр зміщуватиметься праворуч, що, у свою чергу, спричинює збільшення ймовірності помилки другого роду, тобто величини . Різницю називають ймовірністю обґрунтованого відхилення Н0, або потужністю критерію.
Перевірка правильності нульової гіпотези про значення генеральної середньої Для перевірки правильності , де «а» є певним числом, при заданому рівні значущості насамперед необхідно вибрати статистичний критерій K. Найзручнішим критерієм для цього типу задач є випадкова величина K = Z, що має нормований нормальний закон розподілу ймовірностей N(0; 1), а саме
Перевірка правильності нульової гіпотези про рівність двох генеральних середніх (M(X) = M(Y)) Нехай задано дві генеральні сукупності, ознаки яких Х і Y мають нормальний закон розподілу і при цьому незалежні одна від одної. Необхідно перевірити правдивість Тут можуть спостерігатися два випадки: Випадок 1. Обсяг вибірки великий (n > 40) і відомі значення ознак генеральних сукупностей.
Перевірка правильності нульової гіпотези про рівність двох генеральних середніх (M(X) = M(Y)) З кожної генеральної сукупності здійснюють вибірку відповідно з обсягами і будують статистичні розподіли: Тут Обчислюються значення
Перевірка правильності нульової гіпотези про рівність двох генеральних середніх (M(X) = M(Y)) За статистичний критерій береться випадкова величина що має закон розподілу N(0; 1). Оскільки то статистичний критерій набере такого вигляду:
Перевірка правильності нульової гіпотези про рівність двох генеральних середніх (M(X) = M(Y)) Коли , дістанемо: Залежно від формулювання альтернативної гіпотези Н будуються відповідно правобічна, лівобічна та двобічна критичні області. Спостережуване значення критерію відповідно обчислюється: або
Малий обсяг вибірки ( ) i невідомі значення дисперсій генеральної сукупності При малих обсягах вибірок статистичний критерій матиме розподіл Стьюдента з ступенями свободи. У цьому разі для побудови критичних областей критичні точки знаходять за табличними даними.
Критерій узгодженості Пірсона. Критерій узгодженості Пірсона є випадковою величиною, що має розподіл х2, який визначається за формулою і має k = q – m – 1 ступенів свободи, де q — число часткових інтервалів інтервального статистичного розподілу вибірки; m — число параметрів, якими визначається закон розподілу ймовірностей генеральної сукупності згідно з нульовою гіпотезою.
Схожі презентації
Категорії