Презентація на тему:
Роль усних вправ в активізації мислиннєвої діяльності учнів, формуванні навичок пошуку самостійної творчої роботи, їх гармонійного розвитку

Роль усних вправ в активізації мислиннєвої діяльності учнів, формуванні навичок пошуку самостійної творчої роботи, їх гармонійного розвитку “ Предмет математики настільки серйозний, що не слід упускати жодної можливості зробити його більш цікавим “ Блез Паскаль

Комп’ютеризація суспільства, упровадження сучасних інформаційних технологій вимагають від людини математичної грамотності буквально на кожному робочому місці. Це передбачає і конкретні математичні знання, і певний стиль мислення, які формує лише математика.

Однією з форм роботи із перевірених засобів, що сприяють кращому засвоєнню цього предмета в середній школі є систематичне виконання усних вправ та усних обчислень на всіх етапах навчання. Використання усних вправ розвиває у учнів увагу , спостережливість, пам’ять, мову, швидкість реакції, підвищують зацікавленість до навчального матеріалу.

встановлюється ефективний зворотній зв’язок,який дозволяє своєчасно контролювати процес опанування учнями певних знань та вмінь; усні вправи дають можливість вчити великий за обсягом матеріал за короткий проміжок часу; дозволяють учителю судити про готовність класу до вивчення нового матеріалу; про ступінь його засвоєння; допомагають виявити помилки учнів, без великих затрат часу ; багаторазово «програвати» типові ситуації та прийоми міркувань; формувати логічну та мовну культуру учнів. На початку уроку усні вправи допомагають учням швидко включитися в роботу. В середині чи кінці уроку служать своєрідною розрядкою після напруги і втоми, яка з’являється після виконання письмової роботи. За допомогою усних вправ на уроці

Умова вправи сприймається на слух і учні після її виконання усно повідомляють результати; Учні читають умову вправи з підручника, а розв’язують завдання усно; За готовим малюнком і короткою умово геометричні задачі учні знаходять усі необхідні співвідношення між елементами зображеної фігури й називають відповідь; За умовою задачі складають схематичний малюнок чи схематично креслять графік функції, або стислу умову текстової задачі, а розв’язання виконують усно. Усні вправи можна розділити на такі види:

Вправи для актуалізації опорних знань; Вправи для сприйняття й свідомого осмислення навчального матеріалу; Вправи для застосування набутих знань; Усні вправи мають різне дидактичне призначення і їх можна розділити на такі групи:

1. Які з наведених величин можуть бути точними, а які наближеними? У шкільній бібліотеці 5 000 книжок; У класі 32 учні; Відстань від Комсомольська до Полтави 100 км; Довжина спортивної зали 20 м; У коробці 12 олівців. 2. Між якими сусідніми натуральними числами стоїть кожне з чисел: 7,83; 1,3; 154,7; 3,25? 3. Округліть: а) до десятків: 17; 32; 45; 621; 2536 б) до сотень: 246; 4158; 1772; 973 Вправи для актуалізації опорних знань

1. Прочитайте запис і назвіть до якого розряду виконано округлення: а) 9,56927 9,5693; б) 12,363 ≈ 12,36; в) 7,021 ≈ 7,0 г) 0,378 ≈ 0,4 д) 10,1287 ≈ 10,129 2. Округліть: а) до десятих: 17,25; 0,118; 3,573; 125,36 б) до десятків: 21,3; 154,92; 118,915 в) до сотих: 0,546; 12,1895; 813,445 г) до сотень: 158,3; 1845,17; 8172,158 Вправи для сприйняття осмислення нового матеріалу

1. Замість зірочки підставити цифру так, щоб наближена рівність була правильною: а) 216,5* ≈ 216,6; 136,1* ≈ 136,2 1*,2 ≈ 20 б) 151,6* ≈ 151,6 825,* ≈ 825 в) 34,1* ≈ 34,1 825,92* ≈ 825,92 2. Число спочатку округлили до десятків, потім до сотень, потім до тисяч. Чи завжди одержимо той же результат, якщо округлити це число відразу до тисяч? Вправи для застосування набутих знань

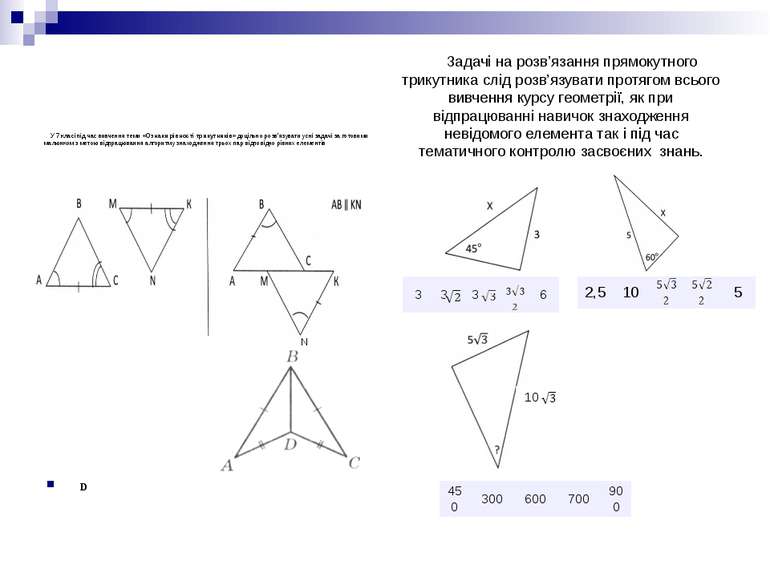
    У 7 класі під час вивчення теми «Ознаки рівності трикутників» доцільно розв’язувати усні задачі за готовими малюнком з метою відпрацювання алгоритму знаходження трьох пар відповідно рівних елементів Задачі на розв’язання прямокутного трикутника слід розв’язувати протягом всього вивчення курсу геометрії, як при відпрацюванні навичок знаходження невідомого елемента так і під час тематичного контролю засвоєних знань. 10 N 3 3 3 6 2,5 10 5 450 300 600 700 900

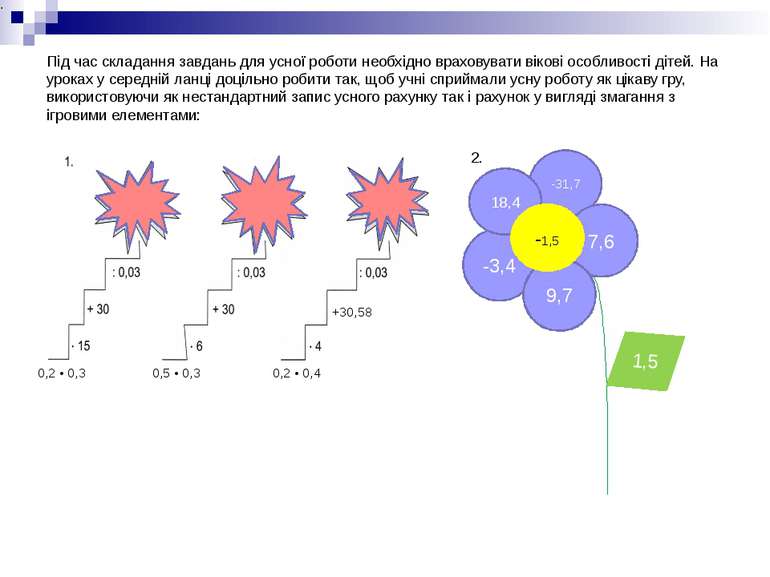
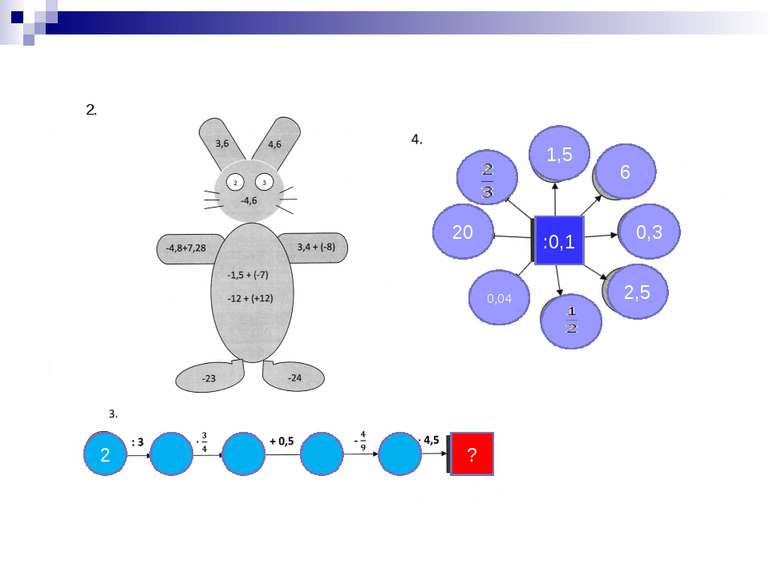
Під час складання завдань для усної роботи необхідно враховувати вікові особливості дітей. На уроках у середній ланці доцільно робити так, щоб учні сприймали усну роботу як цікаву гру, використовуючи як нестандартний запис усного рахунку так і рахунок у вигляді змагання з ігровими елементами: 0,2 • 0,3 0,5 • 0,3 0,2 • 0,4 -31,7 7,6 -3,4 9,7 18,4 -1,5 1,5 2. +30,58

? 2 2. 1,5 6 0,3 2,5 0,04 20 :0,1

Усні обчислення можуть бути максимально варіативними як за змістом так і за формою. Їх можна проводити у вигляді змагання між командами впорядкування відповідей, гри «Сходинки», «Естафета», «Математична розминка», «Математичне лото», «Ланцюжок» тощо. і д о м л ц о Щоб зацікавити учнів під час усної роботи можна зашифрувати відповіді буквами: Розташуйте числа в порядку їх зростання: 8,5 -2,19 -2,9 -15 -9 3 -9,2 Виконання таких вправ активізує пізнавальну діяльність, сприяє розвитку логічного мислення та аналітичних здібностей, стимулює і підвищує інтерес до навчання. Позитивний ефект можна одержати, коли після вивчення математичного факту запропонувати учням самостійно скласти вправи для усного рахунку. Так під час вивчення теми «Подільність чисел» на уроці використати гру «Лабіринт» ( Ознака подільності на 5).

« Математичне лото» Відповіді: 2,76 5 0,24 0,024 28 11,2a 20a 13a 2,8 60,7 85 1,12 0,42,76∙2,5 1,5a + 6,5a =40 0,2∙1,12∙5 13,2a –0,2a 4,3∙0,024 + 5,7∙0,024 8,5a – 8,5b Якщоa-b= 10 13,65a + 6,44 a 1,4a+1,4b Якщоa+b= 20 3,2∙6,07 + 6,8∙6,07

Добре розвинені навички усного рахунку одна із умов успішного навчання учнів в старших класах. У старших класів можуть виникати складнощі моделювання розв’язування текстових задач через не сформованість навичок лічби та навичок пошуку раціональних шляхів обчислень. Концентрація уваги і пошукова активність при розв’язуванні текстових задач знижується, коли учні відволікаються на лічбу як проблемне завдання. Окрім того, не сформованість обчислювальних навичок викликає проблеми не лише на уроках математики, а й при вивчені фізики та інших природничо – математичних дисциплін. Тому формування стійких обчислювальних навичок повинно завжди бути в центрі уваги вчителя. При формуванні навичок усної лічби треба навчити учнів 5 – 6 класів деякими прийомами усних та раціональних обчислень.

5 клас Дії з натуральними числами: Якщо один з доданків збільшити на кілька одиниць, то від суми треба відняти стільки ж одиниць: 364 + 592 = 364 +(592 + 8) -8 = 364 + 600 – 8 =956 Якщо один з доданків збільшити на кілька одиниць, а другий зменшити на стільки ж одиниць, то сума при цьому не зміниться: 997 + 856 = (997 +3 ) + ( 856 – 3) = 1000 + 853 = 1853 Якщо від’ємник збільшити на кілька одиниць і зменшуване збільшити на стільки ж одиниць то різниця не зміниться (аналогічно – «зменшити») 1 351 – 994 = (1 351 + 6) – (994 + 6 ) = 1 357 – 1 000 = 357 Прийоми усних обчислень:

Існують прийоми множення чисел на 5, 11, 25, 93, 97, 98, 99, 125; Множення чисел, близьких до 100 96 ∙ 92 Кожне число доповнюють до 100. Від першого множника віднімають доданок другого множника (96 – 8 = 88), або від другого множника віднімаємо доданок першого (92 – 4 = 88) – це перші дві цифри добутку. Множимо цифри які додавали (4∙8=32) – це останні цифри добутку 96 4 92 8 96 ∙ 92 =8832 88 32 Піднесення до квадрата числа, що закінчується цифрою 5 Перший множник округляємо до десятків з надлишком, а другий – з недостачею. Перемножуємо круглі десятки і до одержаного добутку додаємо 25. 852 = 85 ∙ 85 = 90 ∙ 80 + 25 = 7200 + 25 = 7225 Навички таких обчислень з натуральними числами значно полегшуються множення десяткових дробів. Учні досить швидко виконують завдання типу: 0,64 ∙ 12,5; 10,5 ∙ 10,5; 0,83 ∙ 9,8; 2,44 ∙ 2,5; 0,49 ∙ 9,9 Щоб учні не втрачали інтерес до прийомів усних обчислень такі завдання слід включати до самостійної роботи: (93 ∙ 98 57 ∙ 2) : 45 ∙ (162,375 + 379,625) (848 ∙ 25 – 19 ∙ 1100) : 100

6 клас при вивченні теми «Ознаки подільності чисел» , доцільно, крім обов’язкових показати учням ознаки подільності на 11; 13; Якщо сума цифр, що стоять на непарних місцях відрізняється від суми цифр що стоять на парних місцях на величину яка ділиться на 11, то і число ділиться на 11 1969 ділиться на 11 так як (9 + 9) – (1 + 6) = 11 – ділиться на 11 Число ділиться на 13, якщо на 13 ділиться число, яке дістанемо шляхом закреслення його останньої цифри й до результату додамо число яке дорівнює добутку закресленої цифри на 4 52 ділиться на 13, так як 5 + 2 ∙ 4 = 13 – ділиться на 13

Ще в 5 класі, коли учні вивчають і узагальнюють матеріал початкової школи про дріб, доцільно ознайомити їх з доповнення дробу до 1. звернути увагу на чисельник і знаменник даних пар, зробити потрібний висновок про доповнення дробу до 1, після чого запропонувати вправи 1 - ; 1 - 1 - ; 1 - Перш ніж приступати до виконання дій з мішаними числами, запропонувати записати їх у вигляді суми цілої та дробової частини повторити правило віднімання числа від суми і запропонувати вправи: а) 5 7 б) 5 - ; 6 - Перед вивченням теми « Множення і ділення звичайних дробів доцільно повторити розподільний закон, а потім запропонувати знайти значення виразів: а) 6 б) 22 Під час виконання арифметичних дій з мішаними числами слід привчати учнів спочатку аналізувати умову обираючи раціональний спосіб обчислення: а) (16 б) ( « Дії зі звичайними дробами».

А для того, щоб учні звикли аналізувати вирази перед обчисленнями необхідно їм систематично на хвилинках усної лічби пропанувати вправи типу: а) 15 г) 5 є) ( б) 254 д) 25 ж) 25 в) 26 е) 17

Так у 7 класі вивчення формул скороченого множення розкриває деякі прийоми усних обчислень. Уваги застосовує тотожне перетворення за допомогою формул різниці квадрату ( а2 – а – 1 ) ( а2 + а + 1) не за загальним правилом, а саме за допомогою формули різниці квадратів ( а2 – а – 1 ) ( а2 + а + 1) = ( а2 – (а + 1) ) ( а2 +( а + 1)) = а4 – (а+1)2=а4 –а2 – 2а -1 При розкладанні многочлена 12а2 – 5аb – 3b2 треба добуток 12 ∙ (-3) замінити добутком чисел, сума яких дорівнює -5. Це числа -9 і 4. Таким чином 12а2 – 5аb – 3b2 = 12а2 – 9аb + 4ab – 3b2.

Після розв’язування ряду таких вправ у учнів сформуються стійкі навички, які вже у 8 класі дозволять їм досить швидко скоротити дроби типу: Розглянемо ще приклад добутку раціональних виразів: (х + 1) ( ) Розв’язуючи дану вправу акцентуємо увагу на тому, що значно краще тут застосувати розподільну властивість множення і усно виконавши перетворення й скорочення дробів перейти до додавання дробів яке теж можна виконати усно. Учні, розв’язуючи тестові задачі, складають рівняння: а) х(х-1) =72 - де за умовою задачі х і х-1 – натуральні числа. Отже х1 = 9, х2= 8 б) Дуже добре, якщо в ході незначних аналітичних дій учні знайдуть швидко помилку, допущену при складанні даного рівняння, адже завідомо в лівій частині його є від’ємне число. А подібні помилки при розв’язуванні текстових задач діти допускають досить часто.

А усвідомлений підхід до обчислень, вибір раціональних шляхів міркувань сприяє формуванню мислення та самостійної діяльності учнів, що в свою чергу впливає на формування особистості учнів.