Презентація на тему:
Вписані й описані призми

Вписані і описані призми Геометрія 11 клас Інтегрований курс

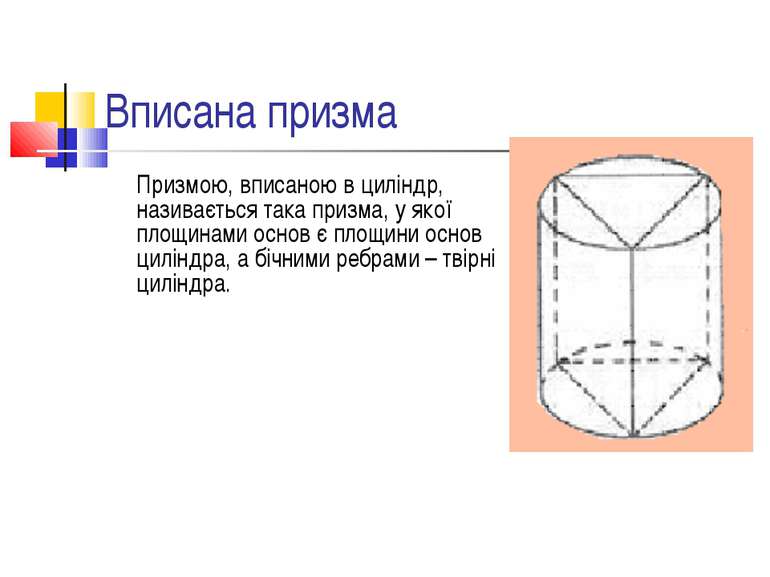
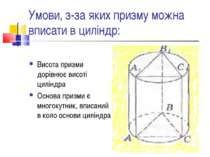
Вписана призма Призмою, вписаною в циліндр, називається така призма, у якої площинами основ є площини основ циліндра, а бічними ребрами – твірні циліндра.

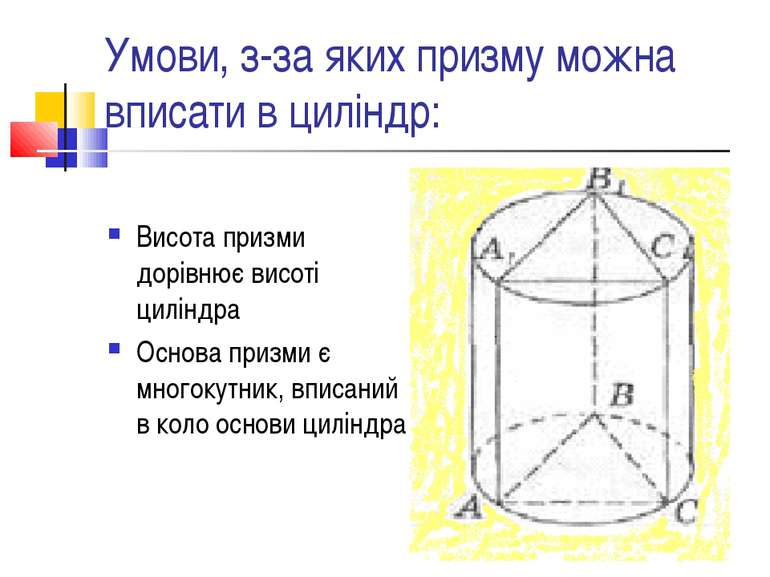
Умови, з-за яких призму можна вписати в циліндр: Висота призми дорівнює висоті циліндра Основа призми є многокутник, вписаний в коло основи циліндра

Оскільки циліндр є прямим, то і призма має бути прямою, за означенням її ребра збігаються з твірними циліндра;основою призми має бути многокутник, який можна вписати в коло. Теорема : призму можна вписати в циліндр, якщо вона пряма і в основі лежить многокутник, навколо якого можна описати коло. Отже, якщо призма є паралелепіпедом, то обов'язково прямокутним, якщо в основі призми лежить трапеція, то ця трапеція – рівнобічна. Радіус кола основи циліндра є радіусом кола, описаного навколо многокутника основи призми.

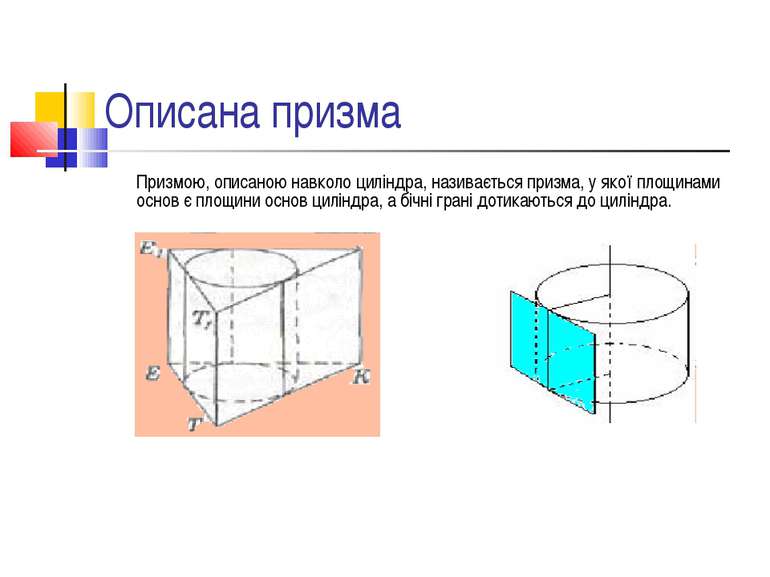
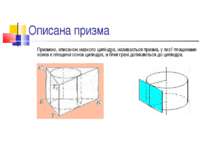
Описана призма Призмою, описаною навколо циліндра, називається призма, у якої площинами основ є площини основ циліндра, а бічні грані дотикаються до циліндра.

Умови, з-за яких призму можна описати навколо циліндра: Висота призми дорівнює висоті циліндра Основа призми є многокутник, описаний навколо кола основи циліндра

Призма має бути прямою, в її основі повинен лежати многокутник, у який можна вписати коло. Якщо це чотирикутник, то суми його протилежних сторін рівні. Якщо цей многокутник – паралелограм, то обов'язково – ромб. Радіус кола основи циліндра є радіусом кола, вписаного в основу призми. Теорема : призму можна описати навколо циліндру , якщо вона пряма і в основі лежить многокутник, в який можна вписати коло. Оскільки навколо довільного трикутника і будь-якого правильного многокутника можна описати коло і в будь-який трикутник та правильний многокутник можна вписати коло, то будь-яку пряму трикутну і будь-яку правильну призму можна вписати в циліндр і описати навколо нього.