Презентація на тему:
«Вписані чотирикутники. Ознака належності чотирьох точок одному колу. Пряма Симсона.

A B C D

Вписані чотирикутники:

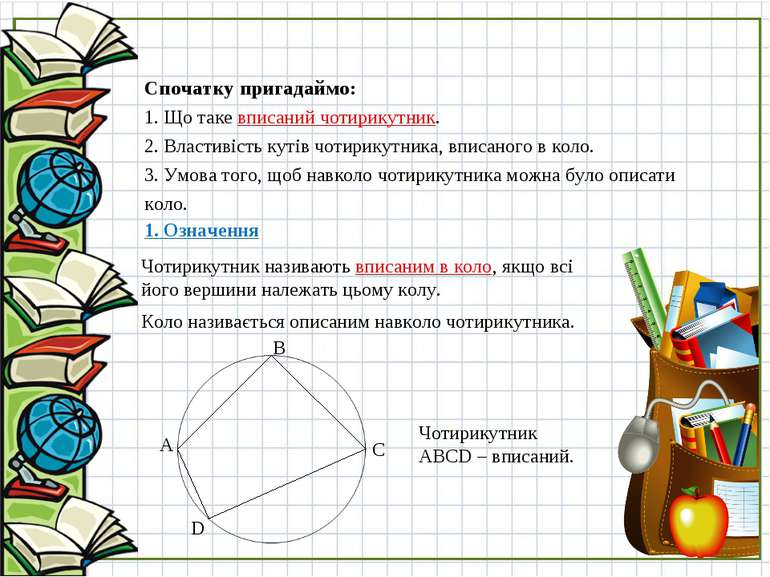
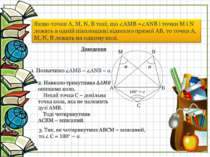
Спочатку пригадаймо: 1. Що таке вписаний чотирикутник. 2. Властивість кутів чотирикутника, вписаного в коло. 3. Умова того, щоб навколо чотирикутника можна було описати коло. 1. Означення Чотирикутник називають вписаним в коло, якщо всі його вершини належать цьому колу. B A D C Чотирикутник ABCD – вписаний. Коло називається описаним навколо чотирикутника.

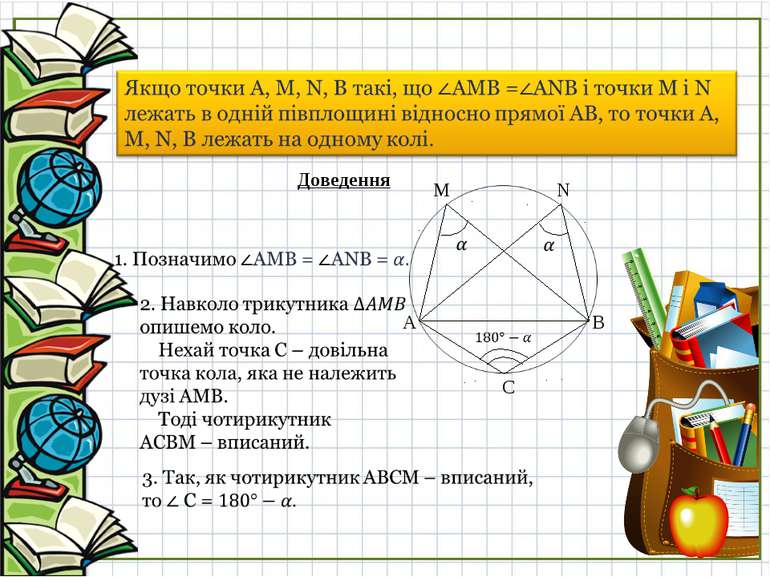
2. Властивість кутів чотирикутника, вписаного в коло. 3. Умова того, щоб навколо чотирикутника можна було описати коло. Згадавши загальну теорію про вписані чотирикутники, почнемо вчити нову тему.

A B С M N Доведення

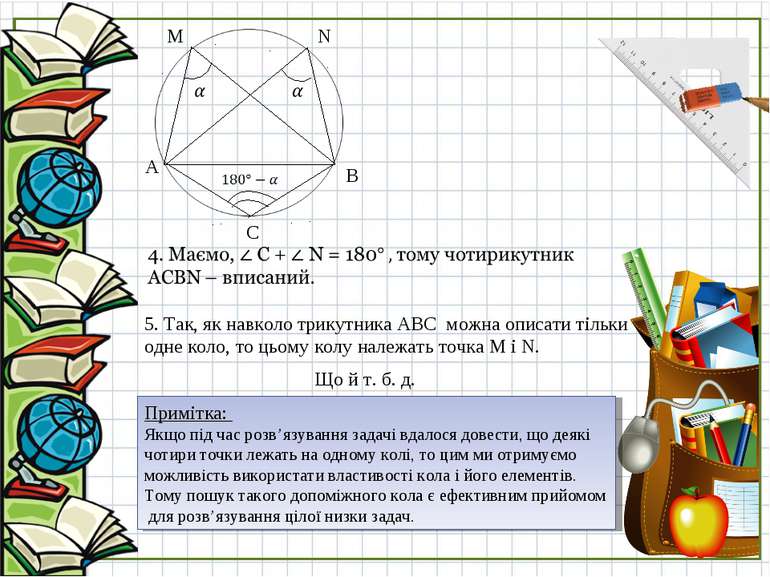
5. Так, як навколо трикутника АВС можна описати тільки одне коло, то цьому колу належать точка M і N. B N С A M Що й т. б. д. Примітка: Якщо під час розв’язування задачі вдалося довести, що деякі чотири точки лежать на одному колі, то цим ми отримуємо можливість використати властивості кола і його елементів. Тому пошук такого допоміжного кола є ефективним прийомом для розв’язування цілої низки задач.

Теорема Основи перпендикулярів, проведених до сторін трикутника ( або їх продовжень ) з довільної точки описаного кола, лежать на одній прямій. Цю пряму називають прямою Симсона. Історія Відкриття цієї прямої тривалий час приписувалося Роберту Сімсону, але насправді вона була відкрита лише в 1797 році Вільямом Уоллесом. Тому з традиційною назвою часто використовується назва пряма Уоллеса.

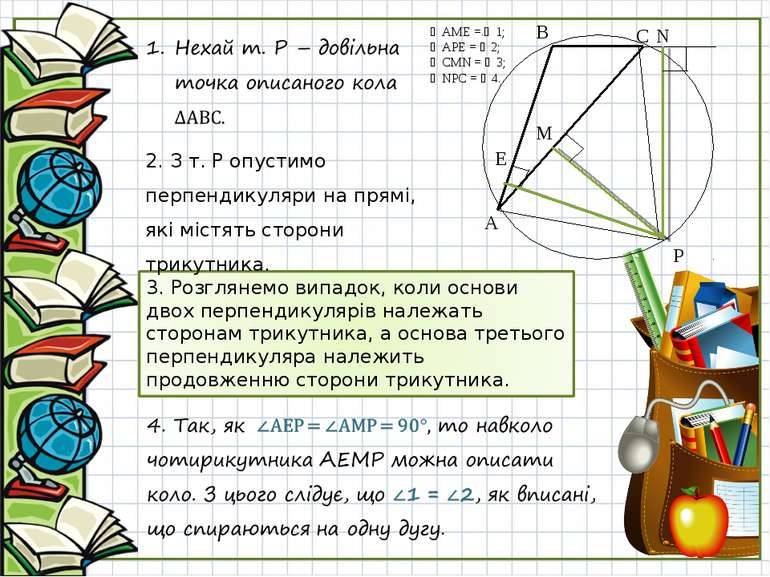
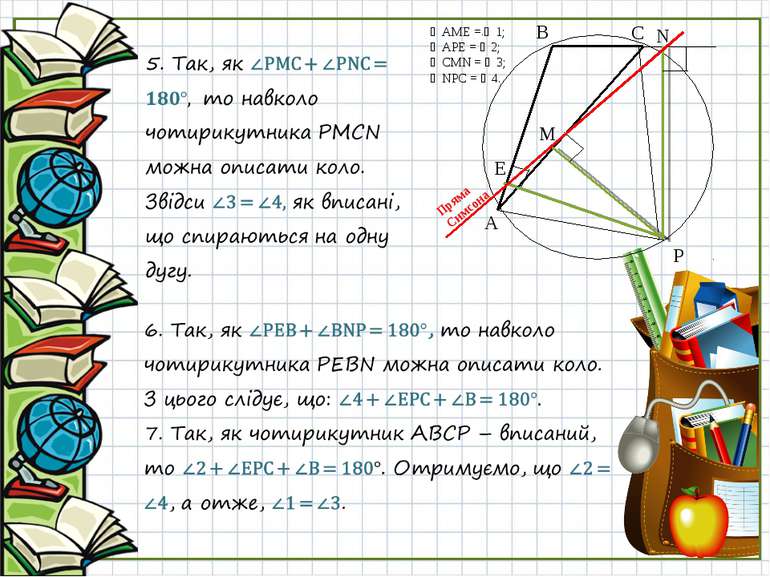
Роберт Сімсон (14 жовтня 1687 — 1 жовтня 1768) — шотландський математик, д-р медицини, професор математики в Глазговському університеті. Доведення P N C B E A M ∠AME = ∠1; ∠APE = ∠2; ∠CMN = ∠3; ∠NPC = ∠4. Пряма Симсона

P N C B E A M ∠AME = ∠1; ∠APE = ∠2; ∠CMN = ∠3; ∠NPC = ∠4. 2. З т. Р опустимо перпендикуляри на прямі, які містять сторони трикутника.

P N C B E A M ∠AME = ∠1; ∠APE = ∠2; ∠CMN = ∠3; ∠NPC = ∠4. Пряма Симсона

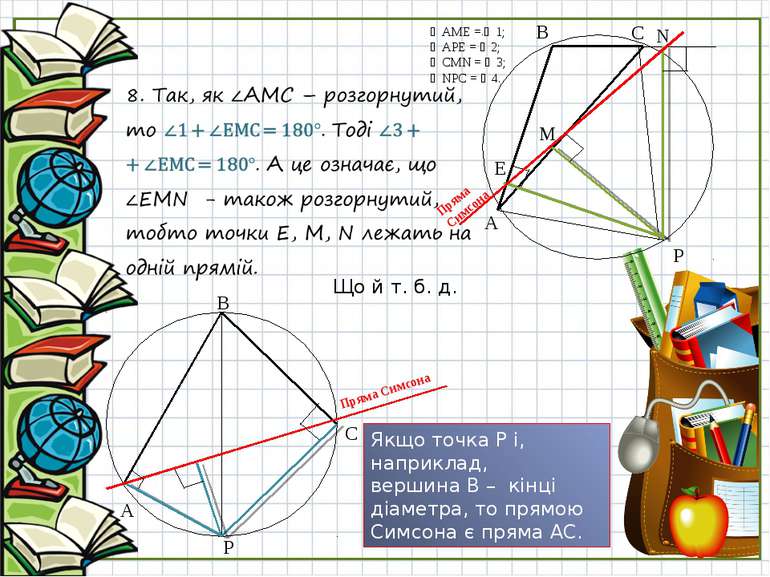
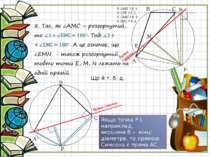
P N C B E A M ∠AME = ∠1; ∠APE = ∠2; ∠CMN = ∠3; ∠NPC = ∠4. Що й т. б. д. P C B A Якщо точка Р і, наприклад, вершина В – кінці діаметра, то прямою Симсона є пряма АС. Пряма Симсона Пряма Симсона

B C A P Ще один випадок, коли основи всіх трьох перпендикулярів, опущених з точки Р на прямі, що містять сторони трикутника, не належать сторонам. Пряма Симсона Справедлива і теорема, обернена до теореми про пряму Симсона: Якщо основи перпендикулярів, опущених з точки Р на прямі, що містять сторони трикутника, лежать на одній прямій, то точка Р належить описаному колу даного трикутника.

Буду дуже рада, якщо моя робота станеться вам в нагоді.