Презентація на тему:
Вписані кути. Вписані та описані чотирикутники

Вписані кути. Вписані та описані чотирикутники Тема 1.2. Трапеція. Теорема Фалеса

Задача 1. Хорда ділить коло у відношенні 5:7. Визначте величини вписаних кутів, що спираються на цю хорду. Нехай хорда АВ ділить коло з центром у точці О у відношенні 5:7. Тоді градусна міра меншої з дуг 360 : 12-5 = 150°, а більшої 360°-150° = 210°. На меншу дугу спирається кут 150°: 2 = 75°, а на більшу — 105° (за теоремою про вписані кути). Відповідь: 75° і 105°. Перевірка домашнього завдання

Задача 2. Точка О — центр кола, описаного навколо рівнобедреного трикутника ABC. Знайдіть кути трикутника ABC, якщо кут АОВ дорівнює 128°. Скільки розв'язків має задача? Нехай трикутник ABC — гострокутний рівнобедрений трикут ник з основою АС (рис. 2, а). Тоді ∠ACB = ∠AOB = 64°. Отже, ∠BAC = 64°, ∠ ABC = 180°- 2∙∠ACB = 180°- 2∙64° = 52°. Якщо основа трикутника — сторона АВ, то ∠ACB = 64°, ∠ А = ∠ В = (180°-64°): 2 = 58°. Якщо трикутник АСВ — тупокутний, тоді ∠ ACS = (360°-128°) :2= 232°:2 = =116°. А оскільки цей трикутник рівнобедрений, то ∠A = ∠B = (180°-116°):2 = 32°.   Відповідь: 1) 64°, 64°, 52°; 2) 64°, 58°, 58°; 3) 116°, 32°, 32°. Перевірка домашнього завдання

Задача 3. Чотирикутник ABCD вписаний в коло. Діагональ АС даного чотирикутника є діаметром кола. Знайдіть кут між діагоналями чотирикутника, що лежить проти сторони AD, якщо ∠ ВАС = 23°, ∠ DAC = 52°. Нехай ABCD — даний чотирикутник, вписаний в коло, АС — діаметр кола. Отже, ∠ B=∠ D= 90°. Нехай К — точка пе ретину діагоналей чотирикутника, тоді шуканий кут — AKD. Кути ВАС і BDC спираються на одну й ту саму дугу та лежать з одного боку від хорди ВС. Отже, ∠BDC = ∠ ВАС = 23°. Оскільки ∠D = 90°, то ∠ADK = 90°- ∠ BDC = 90° - 23° = 67°. У трикутнику АКD ∠ AKD = 180°-(∠ KAD+ ∠ ADK) = 180°- (52°+67°) = 61°. Відповідь: 61°. Перевірка домашнього завдання

Задача 4. Рівнобічна трапеція, один із кутів якої дорівнює 54°, вписана в коло. Кут між діагоналями трапеції, що лежить проти бічної сторони, дорівнює 36°. Знайдіть положення центра кола, описаного навколо трапеції, відносно трапеції. Нехай ABCD — дана рівнобічна трапеція (BC ∥ AD), AB = CD, ∠A = 54°, ∠AKB = 36°. Оскільки трапеція рів нобічна, то ∠ KAD = ∠ KDA = ∠ АКВ: 2 = 36°: 2 = 18° (за властивістю зовнішнього кута трикутника). У трикутнику ABD ∠ABD = 180° - (54°+18°)= 108°. Коло, описане нав коло трапеції ABCD, є описаним і навколо три кутника ABD, який є тупокутним. Тоді центр описаного навколо нього кола розміщений поза трикутником ABD. Аналогічно доводиться, що центр даного кола розміщений і поза трикутником BCD. Отже, і поза трапецією ABCD. Перевірка домашнього завдання

Розв'язання задач за готовими рисунками

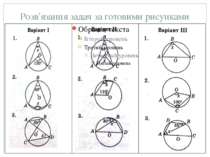
Відповіді до завдань для самоперевірки Відповіді: Варіант I. 1. 60°; 2. 140°; 3. 30°. Варіант II. 1. 80°; 2. 125°; 3. 120°. Варіант III. 1. 90°; 2. 160°; 3. 55°.

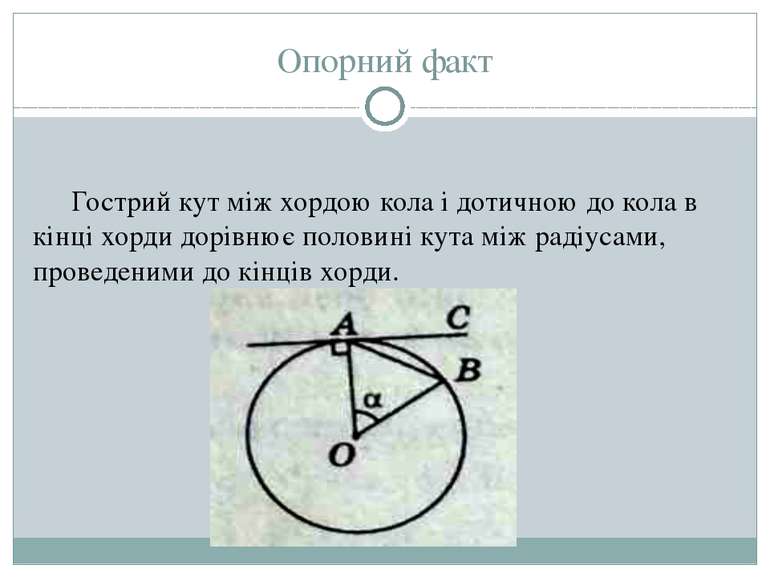
Опорний факт Гострий кут між хордою кола і дотичною до кола в кінці хорди дорівнює половині кута між радіусами, проведеними до кінців хорди.