Презентація на тему:
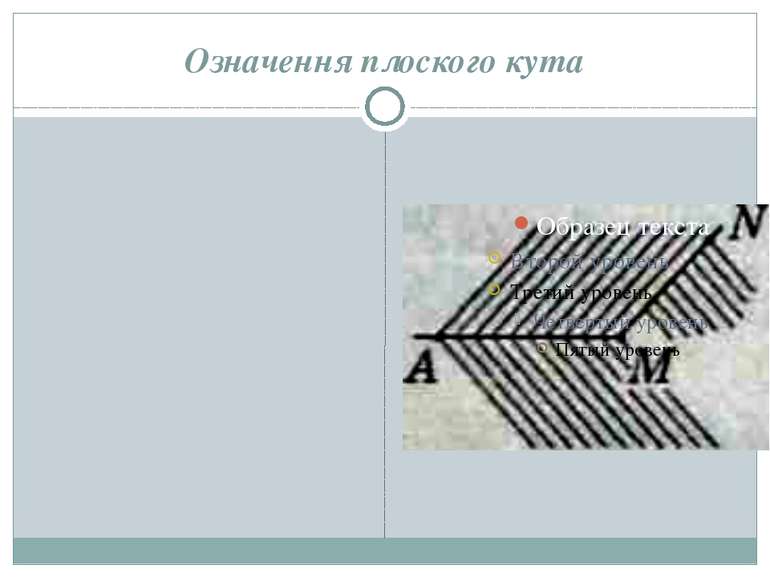
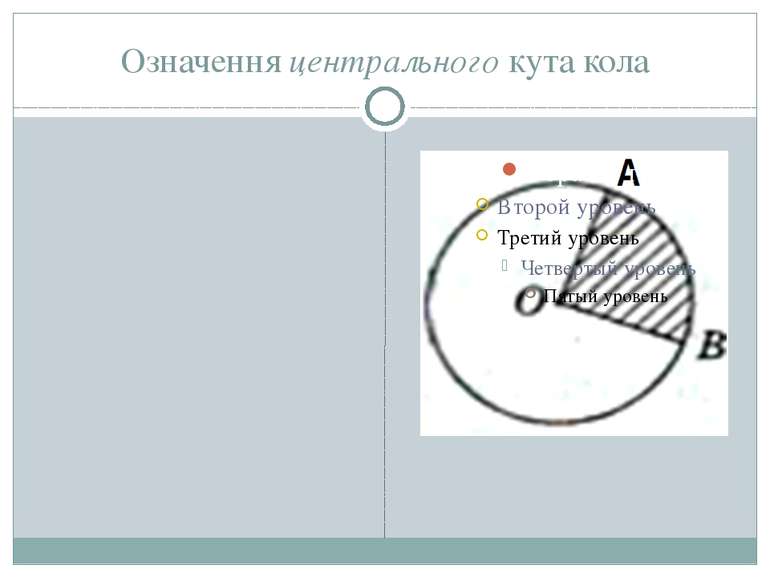
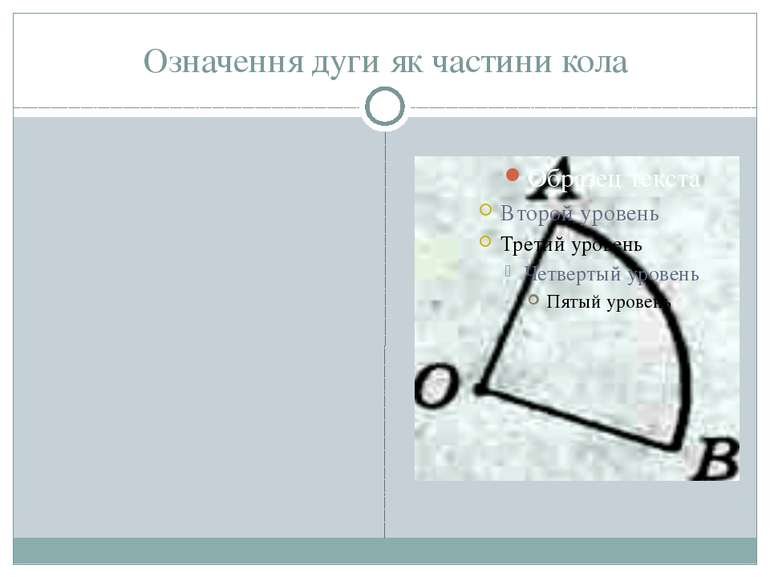
Кути, вписані в коло. Центральний кут

Кути, вписані в коло. Центральний кут Тема 1.2. Трапеція. Теорема Фалеса

Математичний диктант Продовжіть речення: Усі вершини вписаного в коло чотирикутника розташовані на... Сторони чотирикутника, описаного навколо кола, є... Центр кола, описаного навколо чотирикутника, є точкою перетину... Центр кола, вписаного в чотирикутник, є точкою перетину... Коло не можна вписати в чотирикутник, якщо... У паралелограм можна вписати коло за умови, що цей паралелограм є...

Опорні факти Якщо в трапецію вписати коло, то кут, утворений бісектрисами кутів, прилеглих до бічної сторони трапеції,— прямий. У ромб і квадрат завжди можна вписати коло. Його центр є точкою перетину діагоналей. Радіус вписаного в ромб кола у два рази менший за його висоту.

Означення плоского кута

Означення центрального кута кола

Означення дуги як частини кола

Чи є кути вписаними в коло?

Градусна міра дуги кола

Теорема про вписані кути

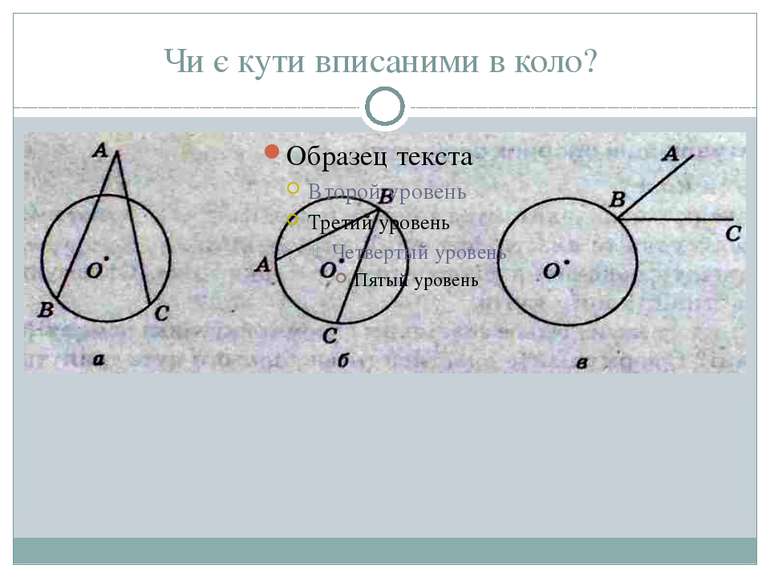
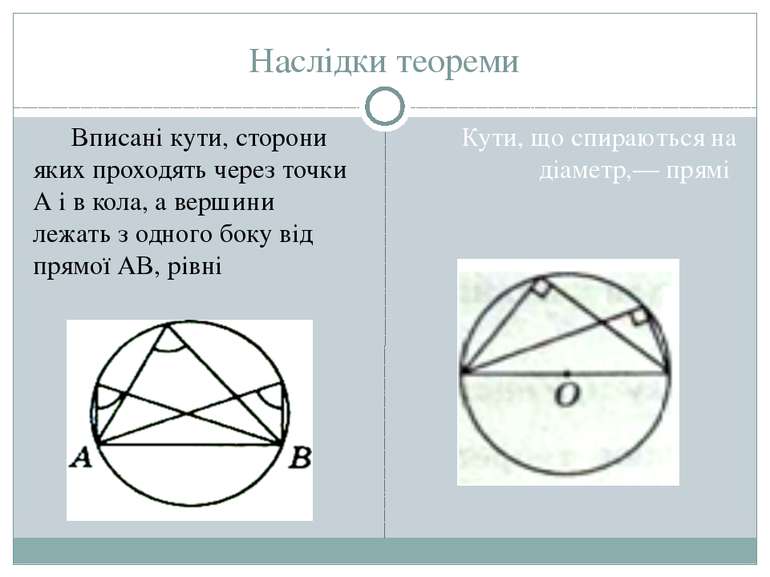
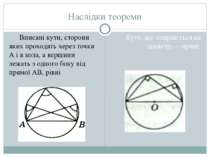
Наслідки теореми Вписані кути, сторони яких проходять через точки А і в кола, а вершини лежать з одного боку від прямої АВ, рівні Кути, що спираються на діаметр,— прямі

Опорні факти Сума протилежних кутів вписаного чотирикутника дорівнює 180° Якщо в чотирикутнику сума двох протилежних кутів дорівнює 180°, то навколо цього чотирикутника можна описати коло.

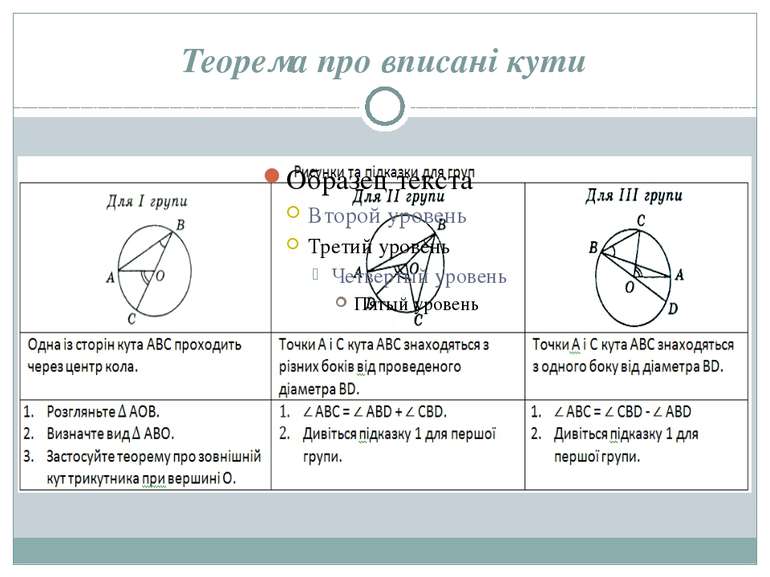
Виконання усних вправ Визначте градусну міри кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює: а) 45°; б) 125°. Визначте градусну міру центрального кута кола, якщо градусна міра відповідного йому вписаного кута дорівнює: а) 15°; б) 87°. У трикутнику ABC ∠ А = 46°, ∠ В = 68°, точка О — центр описаного кола. Знайдіть кути АОВ, ВОС, АОС. Чи можна описати коло навколо чотирикутника ABCD, якщо: а) ∠A = 33°, ∠C = 137°; б) ∠B = 69°, ∠D = 111°; в) ∠A: ∠B: ∠C: ∠D = 5:7:8:4.