Презентація на тему:
"Вектор"

Вектор Підготувала Учениця 5(9) класу Чечет Аліна Тема презентації:

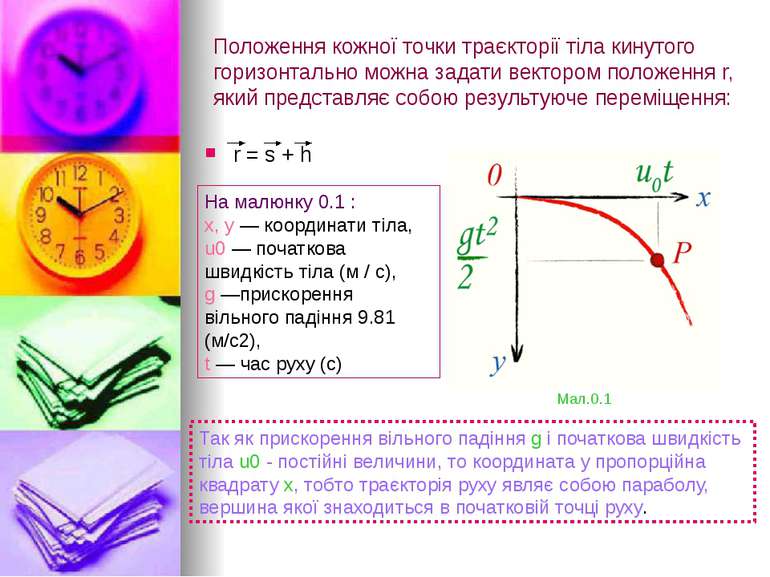
Положення кожної точки траєкторії тіла кинутого горизонтально можна задати вектором положення r, який представляє собою результуюче переміщення: r = s + h На малюнку 0.1 : x, y — координати тіла, u0 — початкова швидкість тіла (м / с), g —прискорення вільного падіння 9.81 (м/c2), t — час руху (c) Так як прискорення вільного падіння g і початкова швидкість тіла u0 - постійні величини, то координата y пропорційна квадрату x, тобто траєкторія руху являє собою параболу, вершина якої знаходиться в початковій точці руху. Мал.0.1

Інтуїтивно вектор розуміється як об'єкт, що має величину, напрям і (необов'язково) точку програми. Зачатки векторного числення з'явилися разом з геометричною моделлю комплексних чисел (Гаусс, 1831). Розвинені операції з векторами опублікував Гамільтон як частину свого кватерніонів обчислення (вектор утворювали уявні компоненти кватерниона). Гамільтон запропонував сам термін вектор (лат. vector, що несе) і описав деякі операції векторного аналізу. Цей формалізм використовував Максвелл у своїх працях з електромагнетизму, тим самим звернувши увагу вчених на нове літочислення. Незабаром вийшли «Елементи векторного аналізу» Гіббса (1880-і роки), а потім Хевісайд (1903) надав векторному аналізу сучасного вигляду.

Гаусс, 1831 Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr2). Иными словами, суммарный поток будет равен: 4πr2 × kq/r2 = 4πkq Это и есть теорема Гаусса.

Гіббса (1880-ті роки) Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному исчислению современный вид. Уже в работах Максвелла кватернионная терминология почти отсутствует, фактически заменённая на чисто векторную. Термин «векторный анализ» предложил Гиббс (1879) в своём курсе лекций.

Хевісайд (1903) Хевісайд розвинув ідею іоносфери, передбачивши існування шару Кеннеллі - Хевісайда. Хевісайд розробив теорію ліній передач (відому як «телеграфні рівняння»). Хевісайд незалежно ввів вектор Пойнтінга і за три роки до Лоренца знайшов вираз для сили Лоренца.

Алгоритм применения векторов при решении геометрических задач состоит из следующих этапов: Выясняем, является ли рассматриваемая задача аффинной или метрической. Если задача аффинная, то, как правило, выбираем произвольный базис или вводим в рассмотрение наименьшее количество векторов, через которые можно выразить все интересующие нас векторы. Если же задача метрическая, то, как правило, выбираем ортонормированный базис. Все, что дано в задаче, записываем с помощью векторов. Все, что необходимо найти или доказать, записываем с помощью векторов.

Из приведенного алгоритма видно, что если задачу можно перевести на язык векторов, то она решается с помощью векторов. И для успешного использования векторной алгебры к решению геометрических задач необходимо уметь переводить геометрические факты на язык векторов или на языке координат.