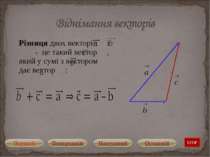Презентація на тему:
ВЕКТОРИ

Виконала: студентка 4 курсу групи БМі Солоненко Марина

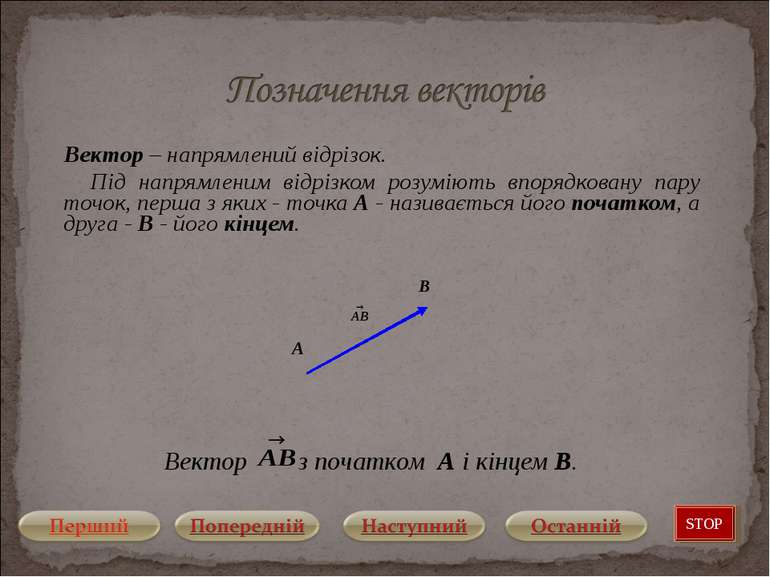
Вектор – напрямлений відрізок. Під напрямленим відрізком розуміють впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем. Вектор з початком A і кінцем B. STOP

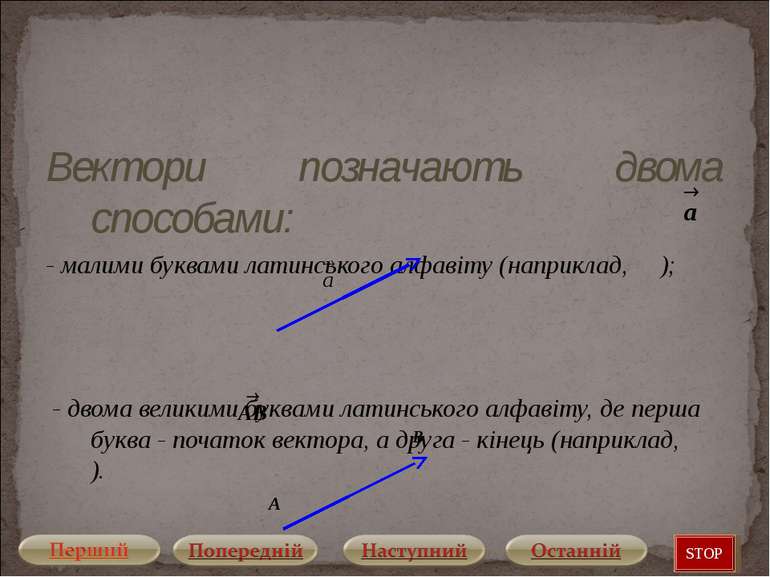
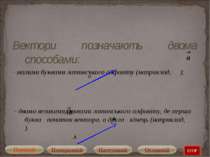
Вектори позначають двома способами: - малими буквами латинського алфавіту (наприклад, ); - двома великими буквами латинського алфавіту, де перша буква - початок вектора, а друга - кінець (наприклад, ). STOP

Чисельне значення вектора називається модулем чи довжиною і позначається Довжина вектора - це довжина відрізка, що зображає цей вектор. Вектори AB і CD називають протилежно напрямленими, якщо протилежно напрямлені півпрямі AB і CD. Вектори AB і CD називають співнапрямленими, якщо співнапрямлені півпрямі AB і CD. STOP

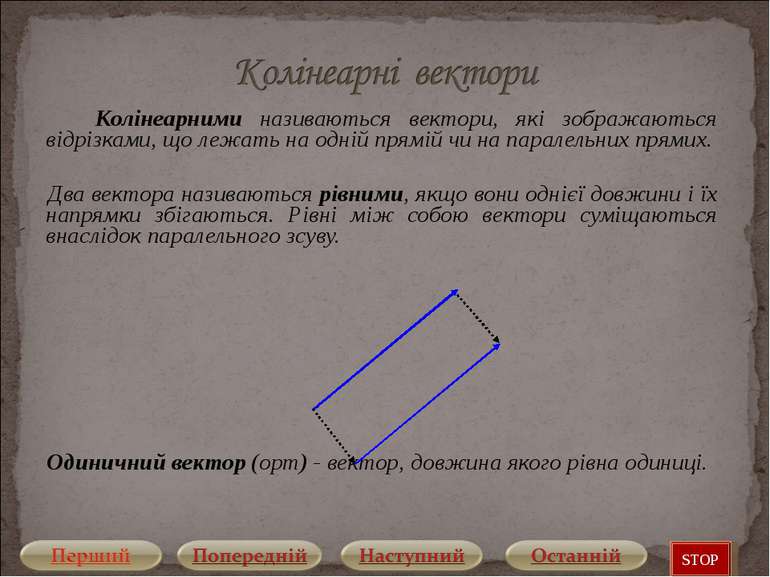
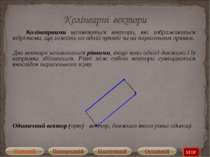
Колінеарними називаються вектори, які зображаються відрізками, що лежать на одній прямій чи на паралельних прямих. Два вектора називаються рівними, якщо вони однієї довжини і їх напрямки збігаються. Рівні між собою вектори суміщаються внаслідок паралельного зсуву. Одиничний вектор (орт) - вектор, довжина якого рівна одиниці. STOP

STOP

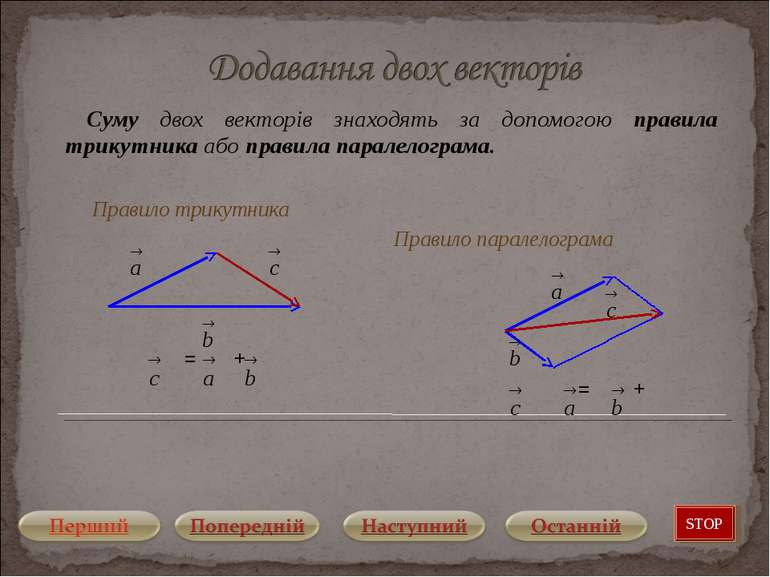
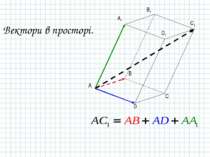
Суму двох векторів знаходять за допомогою правила трикутника або правила паралелограма. Правило трикутника Правило паралелограма = + = + STOP

Суму декількох векторів знаходять за допомогою правила многокутника, яке є узагальненням правила трикутника: STOP

Різниця двох векторів і - це такий вектор , який у сумі з вектором дає вектор : STOP

Добуток вектора на число λ – це колінеарний йому вектор λ співнапрямлений з вектором , якщо λ>0, і напрямлений протилежно йому, якщо λ

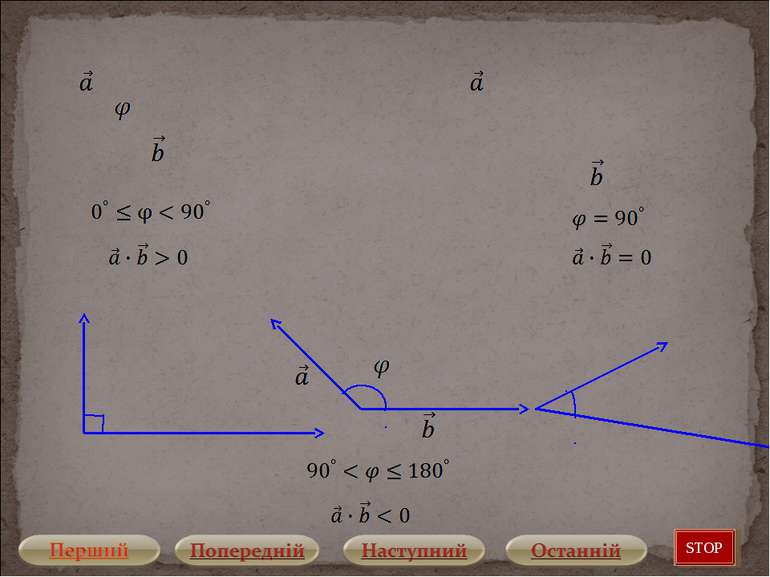
Скалярний добуток ∙ векторів і - це число, що дорівнює добутку модулів векторів на косинус кута між ними: Модуль вектора задовольняє співвідношенню: STOP

STOP