Презентація на тему:
Вектори та їх властивості

Вектори та їх властивості Створили Гурко Катерина та Зінченко Ірина Історична довідка означення вектора Рівні вектори Довжина вектора Додавання векторів теорема Способи побудови суми векторів віднімання векторів Множення вектора на число Скалярний добуток векторів задача фото

Інтерес до векторів і векторного методу виник у математиків у 19ст. через потреби фізики й механіки. Але витоки числення з напрямленими відрізками знаходимо ще в далекій давнині, в роботах піфагорійців і геометричній теорії Евдокса (408-355 до н. е). У геометричному численні, що його виклав Евклід, додавання і віднімання чисел зводилося до відповідних операцій з відрізками, а множення - до побудови прямокутника зі сторонами, довжини яких дорівнюють множникам. У 14-16 ст. геометрична алгебра через обмеженість засобів дослідження майже не розвивалася. Однак у 1587р.фламандський учений Симон Стевін (1548-1620), розглядаючи додавання двох сил у роботі “ Початки статики “, дійшов висновку, що для визначення рівнодійної слід скористатися так званим “ паралелограмом сил “. Для позначення сил Стевін першим увів відрізки зі стрілками. Значно пізніше, у 1803р., французький математик Луї Пуансо (1777-1859) розробив загальну теорію векторів, узагальнивши дослідження попередників. назад

Вектор – це напрямлений відрізок А а В Нульовий вектор – це вектор початок и кінець якого збігаються А.А продовжень назад

Ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих. А В F E А В Вектори АВ і СD називаються спів напрямленими (або однаково напрямленими), якщо промені АВ і СD співнапрямлені . Вектори АВ і СD називаються протилежно напрямленими, якщо промені АВ і СD протилежно напрямлені. назад

Два вектори називаються рівними, якщо вони суміщаються паралельним перенесенням. Властивості й ознаки рівних векторів: 1) Рівні вектори співнапрямлені і мають рівні довжини. 2)Якщо вектори співнапрямлені мають рівні довжини, то вони рівні. 3)Від будь-якої точки можна відкласти вектор що дорівнює даному, і притому тільки один. назад

Довжиною вектора АВ називається відрізок АВ , що зображає вектор. Довжина вектора а ( а ; а ) обчислюється за формулою: а = а + а задача назад

В С С1 Дано: АВСD –паралелограм А1ВС1D- паралелограм Довести:АА1=С1С А1 А D Доведення За правилом трикутника: BC+CC1+C1D=BD BA1+A1A+AD=BD BC+CC1+C1D=BA1+A1A+AD. Оскільки АВСD- паралелограм, то ВС=АD A1BC1D- паралелограм, тому ВА1=C1D,тому СС1=А1А; AA1=C1C Що й треба було довести. назад

Сумою векторів а(а1;а2) і b(b1;b2) називається вектор с(с1;с2) з координатами с1=a1+b1, c2=a2+b2. Властивості додавання векторів: Для будь-яких векторів а(а1;а2), b(b1;b2), c(c1;c1): 1)a+b=b +a; 2)(a+b)+c=a +(b +c); 3)a+0=a назад

Для будь - яких точок А,В і С справджується векторна рівність: АВ+ВС=АС. Доведення Нехай дано точки А(х1;у), В(х2;у2) і С(х3;у3). Виразивши координати векторів-доданків, маємо АВ(х2-х1;у2-у1), ВС(х3-х2;у3-у2). За означенням суми векторів для визначення координат вектора-суми додамо відповідні координати векторів АВ і ВС: х2-х1+х3-х2=х3-х1, у2-у1+у3-у2=у3-у1. Отже, координати вектора-суми збігаються з координатами вектора АС, тобто вектори АВ+ВС і АС рівні. Теорему доведено. назад А(х1;у1) С(х3;у3) В(х2;у2)

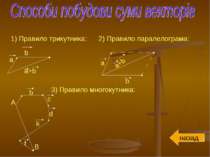
1) Правило трикутника: 2) Правило паралелограма: 3) Правило многокутника: назад a b a+b a b a+b b c d k f A B

Різницею векторів a (a1;а2) і b (b1;b2) називається такий вектор с (с1;с2), який у сумі з вектором b дає вектор а Протилежними векторами називаються два протилежно напрямлені вектори однакової довжини. назад задача a b +c = а b M N O . а - а А В a-b

Дано: Вектори та їх властивості Доведення 1) х і у не колінеарні. х+у х + у , інакше трикутника не існує. 2) х у АВ= х+у, х + у = х + у 3) х у АВ = х, ВС = у х + у = АС, х+у х + у назад В А С x у х х+у x +y Довести: х у А х у В С А В х у

Добутком вектора a(a1;а2) на число k називається вектор ka=(ka1;ka2). Властивості множення вектора на число: Для будь-яких векторів a і b та чисел k,m: 1) ka= ak; 2) (km) a=k (ma); 3) k0=0; 4) 0a=0; 5) (k +m) a= ka +ma; 6) k (a +b)=ka +kb; Довжина вектора ka дорівнює k a . Якщо а 0, то вектор ka співнапрямлений з вектором а за умови k 0 і протилежно напрямлений з вектором а за умови k 0. назад

Скалярним добутком векторів а(а1;а2) і b(b1;b2) називається число a1b1+a2b2. Властивості скалярного множення векторів: Для будь-яких векторів a, b, с та число k: 1) ab=ba ; В 2) (ka) b=k (ab); 3) (a +b) c=ac+ bc; A C Кутом між довільними ненульовими векторами a і b називається кут між векторами, що дорівнюють даним і мають спільний початок. Скалярний добуток векторів дорівнює добутку їх довжин на косинус кута між ними: ab= a b cos (a,b) назад

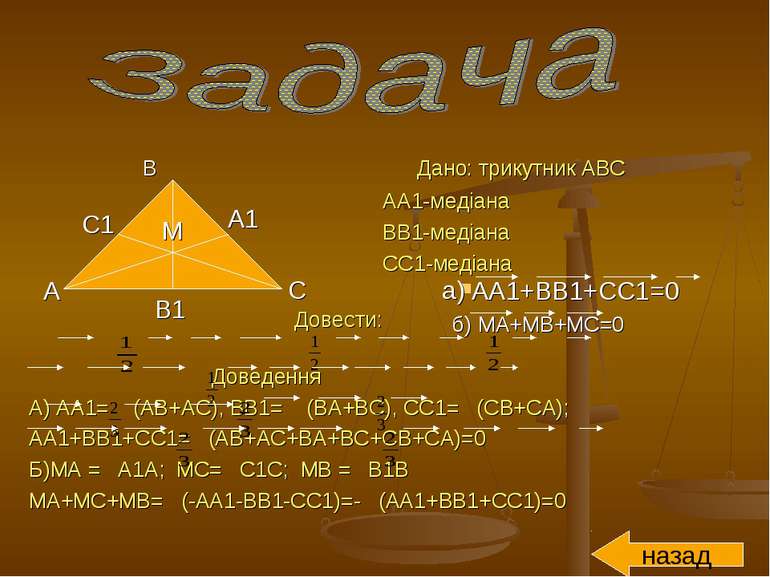
B Дано: трикутник АВС АА1-медіана ВВ1-медіана СС1-медіана Довести: Доведення А) АА1= (АВ+АС), ВВ1= (ВА+ВС), СС1= (СВ+СА); АА1+ВВ1+СС1= (АВ+АС+ВА+ВС+СВ+СА)=0 Б)МА = А1А; МС= С1С; МВ = В1В МА+МС+МВ= (-АА1-ВВ1-СС1)=- (АА1+ВВ1+СС1)=0 назад M C A A1 B1 C1 АА1+ВВ1+СС1=0 а) б) МА+МВ+МС=0

назад