Презентація на тему:
ВИКОРИСТАННЯ ВЕКТОРІВ ПРИ РОЗВ’ЯЗАННІ ГЕОМЕТРИЧНИХ ЗАДАЧ

Данилюк Аліса Михайлівна, учениця 9 класу, Вихрівської ЗОШ І-ІІ ступенів

Науковий керівник: Семкова А.К. Вчитель математики та інформатики

Тема науково-дослідницької роботи: “ВИКОРИСТАННЯ ВЕКТОРІВ ПРИ РОЗВ’ЯЗАННІ ГЕОМЕТРИЧНИХ ЗАДАЧ”

Мета роботи: дослідити метод використання векторів до розв’язання геометричних задач на площині; застосувати даний метод на практиці.

Об’єкт дослідження: теоретичні та практичні аспекти векторного методу розв’язання геометричних задач на площині. Предмет дослідження: розв’язання геометричних задач на площині векторним методом.

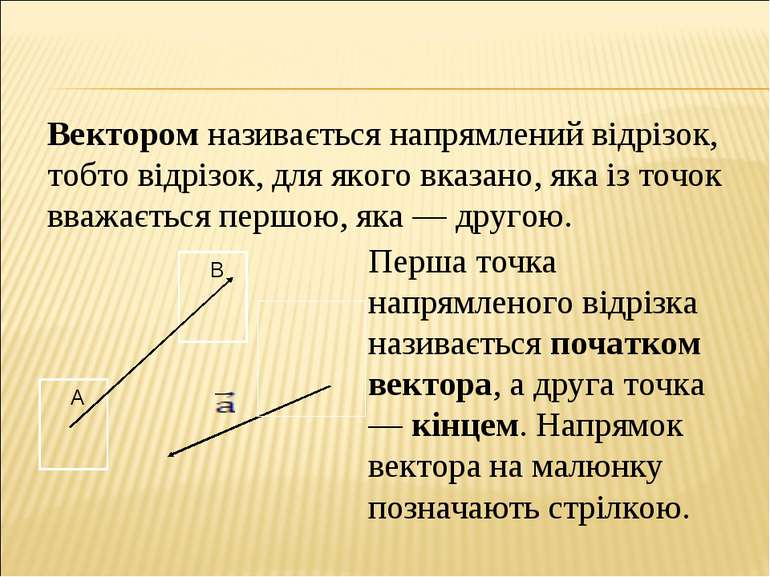
Вектором називається напрямлений відрізок, тобто відрізок, для якого вказано, яка із точок вважається першою, яка — другою. Перша точка напрямленого відрізка називається початком вектора, а друга точка — кінцем. Напрямок вектора на малюнку позначають стрілкою.

D C B A Колінеарними називаються вектори, які зображуються відрізками, що лежать на одній прямій чи на паралельних прямих. Вектори , , попарно колінеарні. Якщо не нульові вектори колінеарні, то вони можуть мати однаковий напрямок, або ж протилежні напрямки. В першому випадку їх називають співнапрямленими, а в другому випадку — протилежно напрямленими.

Довжиною або модулем вектора називається довжина відрізка, що зображує даний вектор. Довжина вектора позначається символом . Два вектори і називаються рівними, якщо виконуються наступні умови: модулі векторів рівні: = ; якщо вектори і не нульові, то вони спів напрямлені.

Правило трикутника. Вектори переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається вектором початок якого збігається з початком першого вектора, а кінець — з кінцем другого вектора. + =

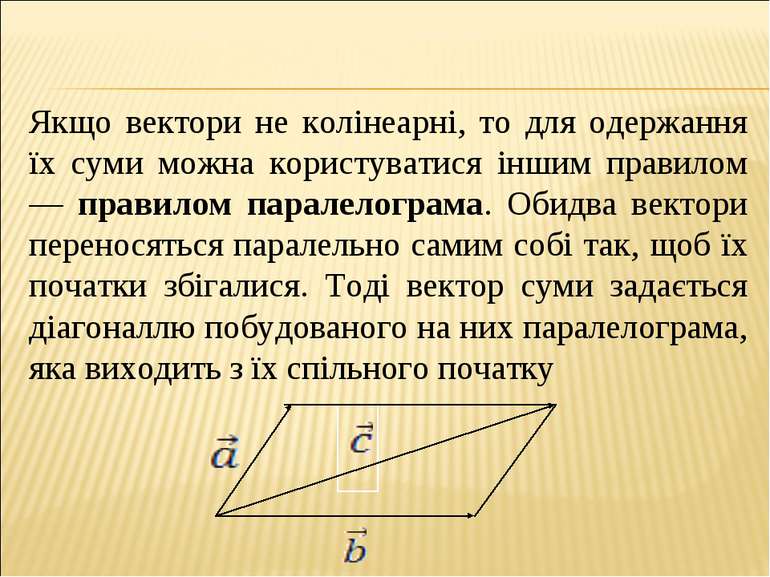
Якщо вектори не колінеарні, то для одержання їх суми можна користуватися іншим правилом — правилом паралелограма. Обидва вектори переносяться паралельно самим собі так, щоб їх початки збігалися. Тоді вектор суми задається діагоналлю побудованого на них паралелограма, яка виходить з їх спільного початку

Добуток не нульового вектора на число називається вектор , який задовольняє умовам: 1) ,де – модуль числа ; 2)Якщо , то і співнапрямлені вектори, якщо , то вектори протилежно напрямлені. Скалярний добуток векторів називається число, що дорівнює добутку довжин цих векторів на косинус кута між ними, тобто

1.Переклад умови задачі мовою векторів, у тому числі: введення в розгляд векторів; вибір системи координат (якщо це необхідно); вибір базисних векторів; розкладання всіх введених векторів на не колінеарні. 2.Запис умови задачі мовою векторів, тобто складання системи векторних рівностей за умовою задачі. 3.Спрощення системи векторних рівностей. 4.Заміна векторних рівностей алгебраїчними рівняннями та їх розв’язування. 5.Пояснення геометричного змісту здобутого розв’язання. Схема розв’язування задач на площині векторним методом:

Міркування в багатьох випадках спрощується, якщо користуватися означенням паралельності в загальному: називати паралельними прямі, які не перетинаються. Тоді для доведення того що існує еквівалентне твердження на векторній мові: існує число , таке що , де — вектори прямих . Доведення паралельності прямих і відрізків

Опираючись на перший пункт, візьмемо за першу пряму , за другу — ми отримуємо твердження, еквівалентне тому, що точки лежать на одній прямій: Враховуючи, що і отримаємо наступне твердження , де — довільна точка. Доведення належності трьох і більше точок одній прямій

Твердження, що точка ділить відрізок в відношенні , тобто , де еквівалентне твердженню або , де — довільна точка. Знаходження відношення, в якому точка ділить відрізок

Доведення перпендикулярності прямих Прямі перпендикулярні тоді і тільки тоді, коли , де , . Знаходження кута між прямими

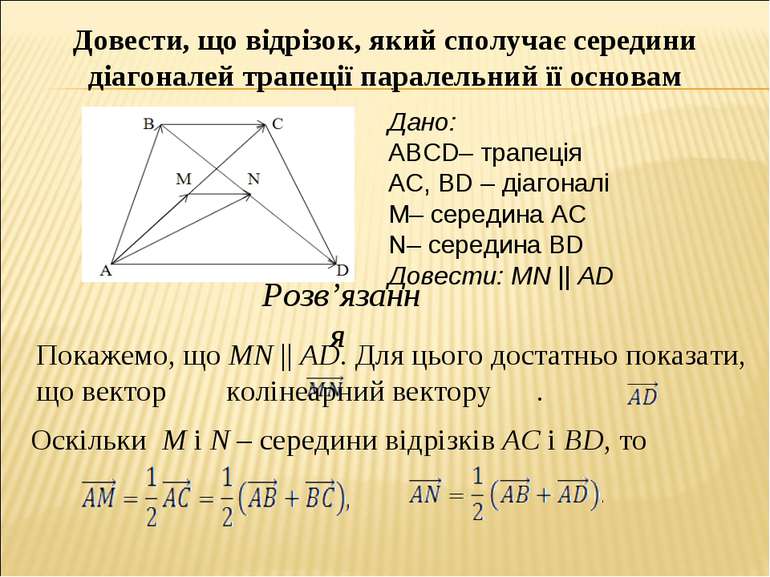
Довести, що відрізок, який сполучає середини діагоналей трапеції паралельний її основам Дано: ABCD– трапеція AC, ВD – діагоналі M– середина AC N– середина ВD Довести: MN || AD . Покажемо, що MN || AD. Для цього достатньо показати, що вектор колінеарний вектору . . Розв’язання Оскільки M і N – середини відрізків AC і BD, то

Звідси, Але вектор колінеарний вектору , тому . Тоді Звідси маємо, що вектори і колінеарні, що потрібно було довести. Отже прямі MN || AD.

Наукова новизна: структуровано та класифіковано геометричні задачі на площині при розв’язанні яких використовуються вектори. Практичне значення роботи: використання векторів до розв’язання геометричних задач на площині, що забезпечує вірність і раціональність розв’язання тієї чи іншої геометричної задачі.