Презентація на тему:
прогресія

1. Дайте означення арифметичної прогресії. Відповідь: Арифметичною прогресією називається числова послідовність, кожний член якої, начинаючи з другого, дорівнює попередньому, до якого додається одне й те ж число.

2. Що називають різницею арифметичної прогресії? Як позначають? Відповідь: це число, яке показує на скільки кожний наступний член більший або менший попереднього. Позначають буквою d.

3. Назвати формулу n-ого члена арифметичної прогресії.

4. Які властивості арифметичної прогресії? Відповідь: Кожний член арифметичної прогресії, починаючи з другого дорівнює середньому арифметичному двох сусідніх з ним членів.

4. Які властивості арифметичної прогресії? Відповідь: Сума будь-яких двох членів скінченної арифметичної прогресії, які рівновіддалені від її крайніх членів, дорівнює сумі крайніх членів цієї прогресії.

6. Які бувають арифметичні прогресії? Відповідь: Якщо в арифметичній прогресії різниця d > 0, то прогресія є зростаючою. Якщо в арифметичній прогресії різниця d

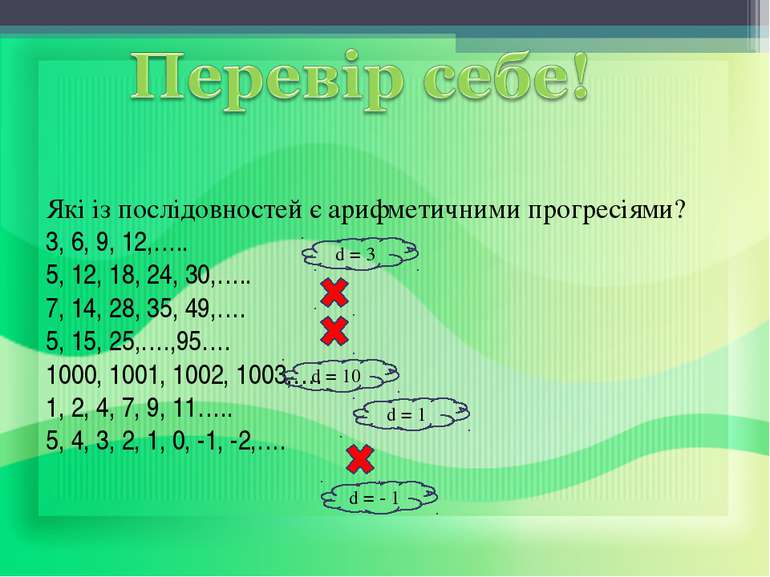
Які із послідовностей є арифметичними прогресіями? 3, 6, 9, 12,….. 5, 12, 18, 24, 30,….. 7, 14, 28, 35, 49,…. 5, 15, 25,….,95…. 1000, 1001, 1002, 1003,…. 1, 2, 4, 7, 9, 11….. 5, 4, 3, 2, 1, 0, -1, -2,…. d = 3 d = 10 d = 1 d = - 1

Знайти різницю арифметичної прогресії: 1; 5; 9……… 105; 100…. -13; -15; -17…… 11; ; 19,….

1. В арифметичній прогресії 2,4; 2,6;… різниця дорівнює 2. 2. Четвертий член арифметичної прогресії 0,3; 0,7; 1,1,… дорівнює 1,5 3. 11-ий член арифметичної прогресії, для якої дорівнює 0,2

Між числами 6 і 21 вставте 4 числа так, щоб разом з даними числами вони утворили арифметичну прогресію. Розв’язання: = 6, = 21, d = (21 – 6)/ (6 – 1)= 3, 6, 9, 12, 15, 18, 21.

Прогресії як часткові види числових послідовностей, трапляються у папірусах II тисячоліття до н.е. На зв’язок між прогресіями вперше звернув увагу великий АРХІМЕД ( 287–212 рр. до н.е)

Найдавнішою задачею, пов’язаною з прогресіями, вважають задачу з єгипетського папірусу Ахмеса Райнда про поділ 100 мір хліба між п’ятьма людьми так, щоб другий одержав на стільки більше від першого, на скільки третій одержав більше другого і т. д . У V ст. до н. е. греки знали слідуючі прогресії і їх суми:

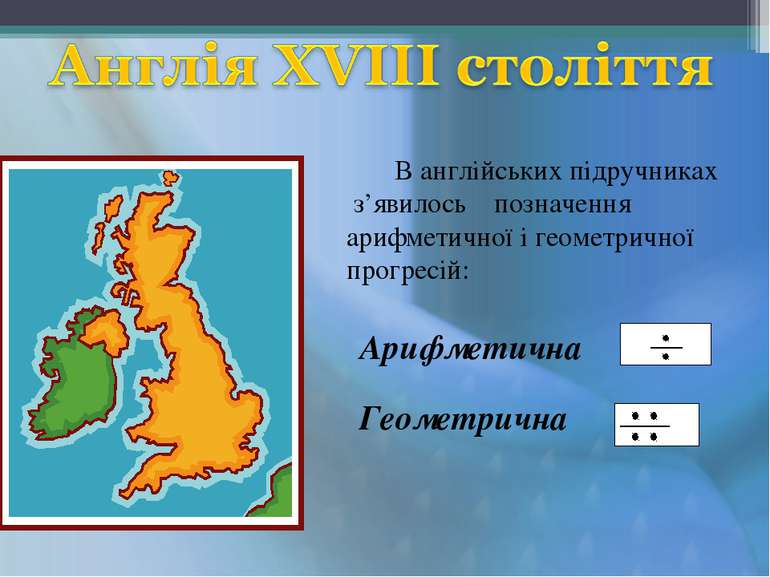
Правило для знаходження суми членів арифметичної прогресії дається у «Книзі абака» (1202 р.) італійського вченого-математика Леонардо Фібоначчі. Правило для суми скінченної геометричної прогресії зустрічається у книзі Н. Шюке «Наука про числа», яка побачила світ у 1484 році. Наука про числа

В англійських підручниках з’явилось позначення арифметичної і геометричної прогресій:

Карл Гаус ( 1777 – 1855 ) Німецький математик, астроном, геодезист, фізик, вважається «королем математики». «Математика – цариця всіх наук, арифметика – цариця математики» Народився 30 квітня 1777 року в герцогстві Брауншвейг у сім’ї садівника. Видатні математичні здібності проявив вже у ранньому дитинстві.

Знайшов моментально суму всіх натуральних чисел від 1 до 100, будучи ще учнем початкової школи. Розв’язання 1 + 2 + 3 + 4 + ….. + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) + ….. = 101 ∙ 50 = 5050

Формула суми n перших членів арифметичної прогресії.