Презентація на тему:
Прогресія

Тема 6 Арифметична та геометрична прогресії Числові послідовності. Властивості числових послідовностей Арифметична прогресія. Формула n-го члена арифметичної прогресії Сума перших n членів арифметичної прогресії Геометрична прогресія. Формула n-го члена геометричної прогресії Сума перших n членів геометричної прогресії Нескінченна геометрична прогресія (|q| < 0) та її сума Розв’язування вправ

Пункт 10.2. Прогресії як часткові види числових послідовностей, трапляються у папірусах II тисячоліття до н.е. На зв’язок між прогресіями вперше звернув увагу великий АРХІМЕД ( 287–212 рр. до н.е) Арифметична прогресія. Формула n-го члена арифметичної прогресії

Древній Єгипет Найдавнішою задачею, пов’язаною з прогресіями, вважають задачу з єгипетського папірусу Ахмеса Райнда про поділ 100 мір хліба між п’ятьма людьми так, щоб другий одержав на стільки більше від першого, на скільки третій одержав більше другого і т. д . У V ст. до н. е. греки знали слідуючі прогресії і їх суми: Арифметична прогресія. Формула n-го члена арифметичної прогресії

Правило для знаходження суми членів арифметичної прогресії дається у «Книзі абака» (1202 р.) італійського вченого-математика Леонардо Фібоначчі. Правило для суми скінченної геометричної прогресії зустрічається у книзі Н. Шюке «Наука про числа», яка побачила світ у 1484 році. Наука про числа Цікаво знати

В англійських підручниках з’явилось позначення арифметичної і геометричної прогресій: Англія XVIII століття Геометрична

Арифметична прогресія. Формула n-го члена арифметичної прогресії

Поняття арифметичної прогресії Розглянемо числові послідовності та звернемо увагу на їх особливості: а) 7; 10; 13; 16; 19; (а — діаметри шківів (у см), насаджених на спільний вал). Кожен член цієї послідовності, починаючи з другого, можна отримати, додавши до попереднього члена число 3. б) 6; 4,5; 3; 1,5; 0; -1,5; ... У послідовності кожен член, починаючи з другого, можна отримати, віднявши 1,5 від попереднього члена (або додавши до попереднього члена -1,5). Такі послідовності називають арифметичною прогресією.

Поняття арифметичної прогресії Числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому членові, до якого додають одне і те саме число, називається арифметичною прогресією. Інакше кажучи, числова послідовність a1 , a2 , а3, ..., аn, ... є арифметичною прогресією, якщо для будь-якого натурального числа n виконується умова an+1 = a n + d. З цієї рівності випливає рівність an+1 - a n = d яка означає, що різниця між будь-яким наступним і попереднім членами арифметичної прогресії дорівнює одному і тому самому числу, яке тому і називають різницею прогресії (d). Якщо різниця прогресії d > 0, то прогресія є зростаючою, якщо різниця d < 0, то прогресія є спадною, а при d = 0 — сталою.

Поняття арифметичної прогресії Приклад 1. прогресія 20; 24; 28; ... є зростаючою (d = 4 > 0); Приклад 2. прогресія 11; 8; 5; ... є спадною (d = -3 < 0); Приклад 3. прогресія 2; 2; 2; ... є сталою (d = 0).

Формула загального члена арифметичної прогресії Нехай маємо арифметичну прогресію: -12; -8; -4; 0; 4; ... . Закономірність утворення її членів очевидна: в даному випадку різниця прогресії d = 4. Продовжуючи додавати це число до кожного нового члена прогресії, можемо обчислити значення її члена, який стоїть на будь-якому місці (з будь-яким порядковим номером). Однак цей шлях громіздкий і не досить раціональний. Уявімо, скільки потрібно виконати обчислень, щоб знайти значення, наприклад, сотого члена даної прогресії.

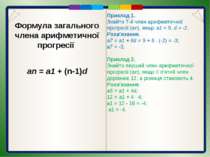
Формула загального члена арифметичної прогресії аn = а1 + (n-1)d З означення арифметичної прогресії випливає: а2 = а1 + d а3 = а2 + d = (а1 + d) + d = а1 + 2d; а4 = а3 + d = (а1 + 2d) + d = a1 + 3d; а5 = а4 + d = (а1 + 3d) + d = а1 + 4d і т.д. Аналізуючи здобуті формули, помічаємо, що відповідний член прогресії отримують додаванням до першого її члена а1 різниці прогресії d, помноженої на число, яке на 1 менше від порядкового номера шуканого члена. Поширюючи за аналогією цей висновок на наступні члени , можемо записати, що аn = а1 + (n-1)d. Таким чином, ми отримали формулу загального члена арифметичної прогресії.

Формула загального члена арифметичної прогресії аn = а1 + (n-1)d Приклад 1. Знайти 7-й член арифметичної прогресії (аn), якщо а1 = 9, d = -2. Розв'язання. а7 = а1 + 6d = 9 + 6 (-2) = -3; а7 = -3. Приклад 2. Знайти перший член арифметичної прогресії (аn), якщо її п'ятий член дорівнює 12, а різниця становить 4. Розв'язання. а5 = a1 + 4d; 12 = а1 + 4 4; а1 = 12 - 16 = -4; а1 = -4.

Формула загального члена арифметичної прогресії аn = а1 + (n-1)d Приклад 3. Знайти перший член і різницю арифметичної прогресії (аn), якщо а6 = 18 і а11 = З0. Розв'язання. Знайдемо d. а6 = а1 + 5d, a11 = а1 + 10d; a11 - а6 = (а1 + 10d ) - (а1 + 5d) = 5d; 30-18 =5d, d = 2,4 Знайдемо а1 : а6 = а1 + 5d 18 = а1 + 5 2,4; 18 = а1 + 12; а1 =18 - 12 = 6; a1 = 6. Відповідь. a1 = 6, d = 2,4.

Запитання для самоперевірки Яку числову послідовність називають арифметичною прогресією? Що таке різниця арифметичної прогресії? Як обчислити будь-який член арифметичної прогресії, знаючи її перший член і різницю? Чи правильне твердження: арифметичну прогресію можна задати її першим членом і різницею прогресії? Чи правильне твердження: арифметичну прогресію задають будь-які два її члени?

Первинне закріплення вивченого матеріалу 471. Які з послідовностей є арифметичними прогресіями: а) 2; 5; 8; 11; ...; б) 2; 6; 12; 24;...; в) 7; 4; 1; -2;...; г) 1; 2; 3; 5; 8;... ? 472°. Сходи, що ведуть на веранду, мають 8 східців. Перший східець — бетонна плита заввишки 10 см; усі інші східці мають висоту 15 см. На якій висоті від землі розташовані 2-й, 3-й, 4-й східці та підлога веранди?

Первинне закріплення вивченого матеріалу 483. На стороні АВ кута ABC відкладено рівні відрізки BA1 , А1С4 , А2С3, ..., А7С8 і через їхні кінці проведено паралельні прямі до перетину зі стороною ВС. Довжина відрізка А1С1 дорівнює 2,5 см. Знайдіть довжину відрізків А4С4 і А8С8

Запитання для самоперевірки Запитання для самоперевірки

Первинне закріплення вивченого матеріалу Первинне закріплення вивченого матеріалу

Первинне закріплення вивченого матеріалу Первинне закріплення вивченого матеріалу