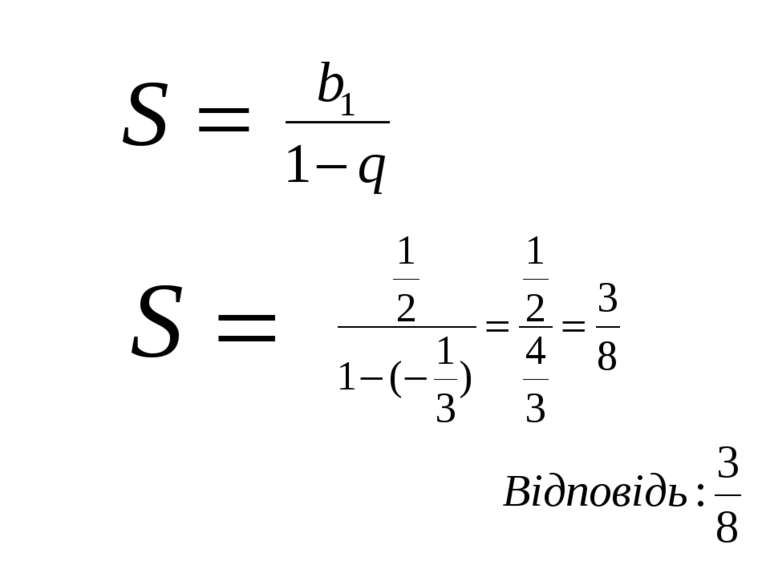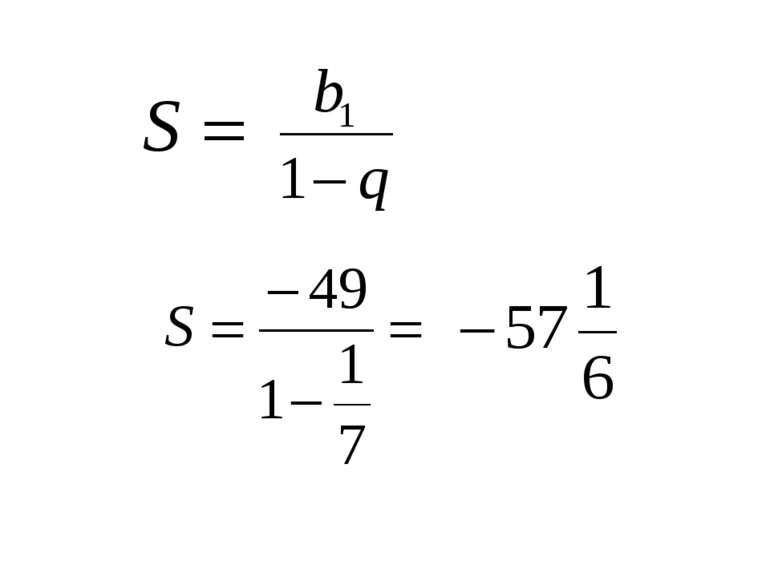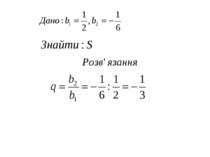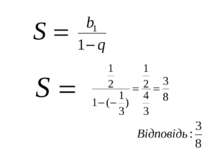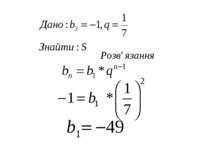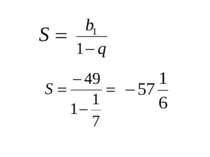Презентація на тему:
Арифметична та геометрична прогресія

Тема 6 Арифметична та геометрична прогресії Числові послідовності. Властивості числових послідовностей Арифметична прогресія. Формула n-го члена арифметичної прогресії Сума перших n членів арифметичної прогресії Геометрична прогресія. Формула n-го члена геометричної прогресії Сума перших n членів геометричної прогресії Нескінченна геометрична прогресія (|q| < 0) та її сума Розв’язування вправ

Готуємося до уроку Використано матеріали Бібліотеки електронних наочностей “Алгебра 7-9 клас”. Робота вчителя СЗОШ І- ІІІ ступенів № 8 м. Хмельницького Кравчук Г.Т. Мультимедійні технології на уроках алгебри 2011 рік

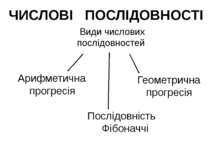
Види числових послідовностей Арифметична прогресія Геометрична прогресія Послідовність Фібоначчі ЧИСЛОВІ ПОСЛІДОВНОСТІ

Італійський купець і мандрівник , син міського писаря ,Леонардо із Пізи (1180-1240р.) , більш відомий під прізвищем Фібоначчі ,був одним із найвідоміших математиків середньовіччя. Роль його книг у розвитку математики і поширенню у Європі математичних знань важко переоцінити. Життя і наукова кар’єра Леонардо тісно пов’язані з розвитком європейської культури і науки. Леонардо Пізанський (Фібоначчі)

При розв’язуванні однієї задачі про можливість кількості народження кроликів від однієї пари через рік, він одержав ряд чисел:1,1,2,3,5,8,13,21,34,55…. Особливістю цієї послідовності чисел є те, що кожний її член, починаючи з третього, дорівнює сумі двох попередніх, а відношення сусідніх чисел ряду наближається до відношення золотого перерізу, який дуже хвилював голови того часу. Так, 21:34=0,617, а 34:55=0,618

Математичний диктант 1.У геометричній прогресії перший член дорівнює 32, другий дорівнює 8. Знайти знаменник цієї прогресії. 2. Знайти шостий член геометричної прогресії, знаючи, що її перший член дорівнює 3, а знаменник дорівнює 2. 3. Знайти перший член геометричної прогресії, якщо, її п’ятий член дорівнює 125, а знаменник дорівнює 5. 4. 3; 6… - геометрична прогресія. Знайти суму шести її членів.

Перевір себе ! 1. 1/4 2. 96 3. 1/5 4. 189

Знайти знаменник геометричної прогресії:

Пункт 11.3. Нескінченна геометрична прогресія (|q| < 0) та її сума Розглянемо геометричні прогресії: Усі вони — нескінченні, і знаменник q кожної з них такий, що |q| < 1. Їхньою особливістю є те, що зі збільшенням номера члена прогресії його значення дедалі менше відрізняється від нуля (кажуть: “значення членів прогресії bn прямують до нуля при необмеженому зростанні n”, а записують так:

Нескінченна геометрична прогресія (|q| < 0) та її сума Розглянемо, що відбувається із сумою n перших членів таких прогресій при необмеженому зростанні n. За відомою формулою

Нескінченна геометрична прогресія (|q| < 0) та її сума Вираз вважають сумою нескінченної геометричної прогресії з першим членом b1 і знаменником q, де |q| < 1. Позначивши цю суму буквою S, можна записати:

Нескінченна геометрична прогресія (|q| < 0) та її сума Приклад 1. Обчислити суму – Розв'язання. Маємо суму членів нескінченної геометричної прогресії, в якої Скориставшись формулою , маємо: Отже,

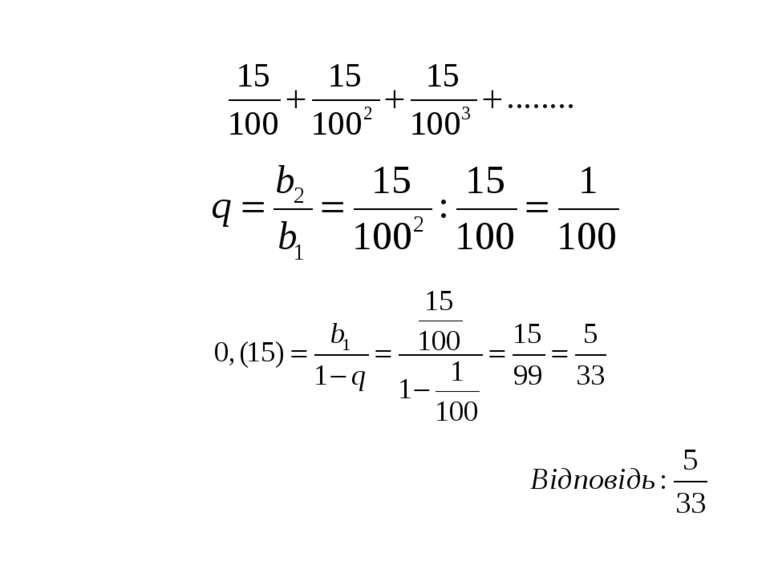
Нескінченна геометрична прогресія (|q| < 0) та її сума Приклад 2. Періодичний дріб 0,151515… записати у вигляді суми членів нескінченної геометричної прогресії і знайти цю суму. Розв'язання. Маємо: 0,(15) = У прогресії Отже,

Нескінченна геометрична прогресія (|q| < 0) та її сума Приклад 3. Періодичний дріб 0,2777... перетворити у звичайний. Розв'язання. 0,2777 = Розглянуті приклади 2 і 3 показують, як періодичні десяткові дроби можна записати у вигляді звичайних.

Узагальнююче повторення вивченого матеріалу

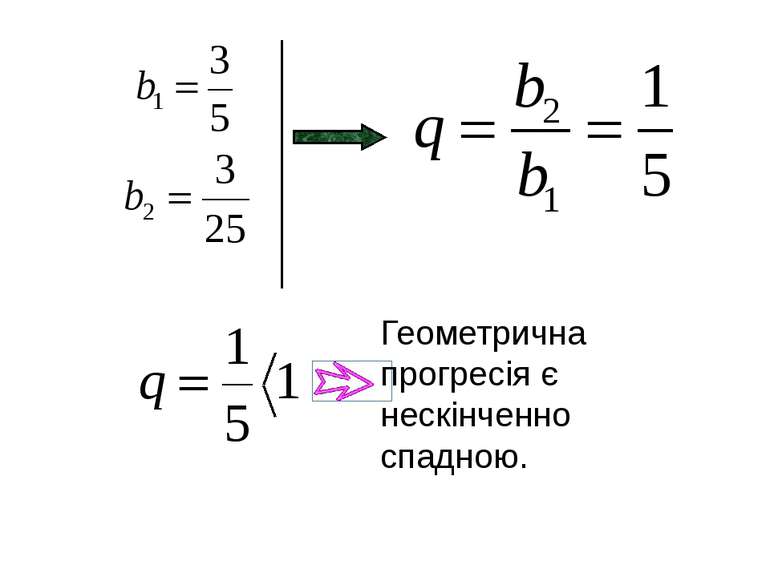
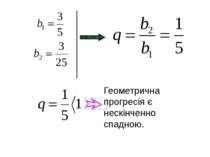
Геометрична прогресія називається нескінченно спадною, якщо модуль знаменника менший за одиницю.

Довести, що геометрична прогресія є нескінченно спадною. Доведення.

Геометрична прогресія є нескінченно спадною.

Сума нескінченно спадної геометричної прогресії

Записати нескінченний періодичний десятковий дріб 0,(15) = 0,151515… у вигляді звичайного дробу.

0,(15) = 0,151515… Складемо послідовність наближених значень :

0,(15) = 0,151515… Складемо послідовність наближених значень :