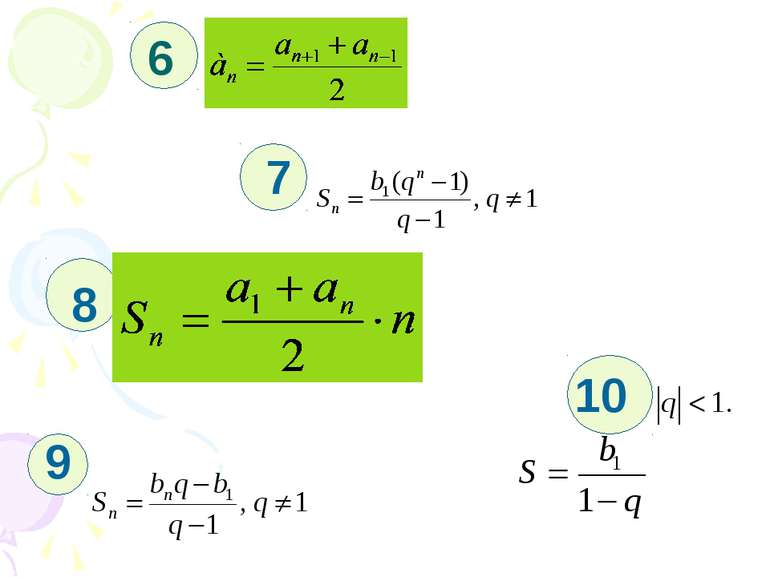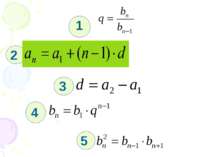Презентація на тему:
Арифметична та геометрична прогресії

узагальнюючий урок по темі Робота Резник О.В. вчителя математики та фізики Загальноосвітньої школи І-ІІІ ступенів №9 м. Шостки

ПЛАН УРОКУ Організаціно - вступна частина. Перевірка домашнього завдання. Мотивація навчальної діяльності. Повторення та систематизація знань учнів по темі. Підсумки уроку. Домашнє завдання.

Немає жодної галузі математики, хоч би якою абстрактною вона не була, що коли-небудь не буде застосованою до явищ дійсного світу. М.І.Лобачевський

найціннішим є використання набутих знань у життєвих ситуаціях.

1. Що називають числовою послідовністю? 2. Які способи задавання числових послідовностей ви знаєте? 3. Означення арифметичної прогресії. 4. Чи можна вважати арифметичну прогресію заданою, якщо відомі її перший член і різниця? Визначення геометричної прогресії. У якому випадку можна вважати геометричну прогресію заданою? 7. Які геометричні прогресії вам відомі?

Вірне чи хибне висловлювання ? 1. В арифметичній прогресії 2,4; 2,6; … різниція дорівнює 2. 2. В геометричній прогресії 0,3 ; 0,9 ; … третій член дорівнює 2,7 3. 11-ий член арифметичної прогресії, у якої дорівнює 0,2

4. Сума 5 перших членів геометричної прогресії, у якої дорівнює 11. 5. Послідовність чисел, кратних 5, є геометричною прогресією. 6. Послідовність степенів числа 3 - це арифметична прогресія.

1. В арифметичній прогресії 2,4; 2,6;… різниція дорівнює 2 d = 2,6 – 2,4 = 0,2, 2. істинне 3. В геометричній прогресії 0,3; 0,9;… третій член дорівнює 2,7 11-ий член арифметичної прогресії, у котрій дорівнює 0,2 хибне хибне

4. Сума 5 перших членів геометричної прогресії, у якої дорівнює 11. 5. 5; 10; 15;… - арифм. прогресія хибне. 6. Послідовність степенів числа 3 -це арифметична прогресія. 3; 9; 27;…- геометрична прогресія істинне Послідовність чисел, кратних 5,є геометричною прогресією. хибне

Частина 2

1 5 3 2 4

6 1 1 1 1 1 7 8 9 10

Назва формули Різниця арифметичної прогресії 3 Знаменник геометричної прогресії 1 Формула n -члена арифметичної прогресії 2 Формула n – члена геометричної прогресії 4 Властивість членів арифметичної прогресії 6 Властивість членів геометричної прогресії 5 Сума n -членів арифметичної прогресії 8 Сума n- членів геометричної прогресії 7,9 Сума членів нескінченної геометричної прогресії 10

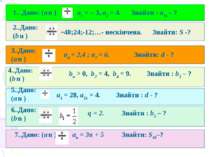
1.. Дано: (а n ) а1 = – 3, а2 = 4. Знайти : а16 – ? 2..Дано: (b n )  , -48;24;-12;…- нескінчена. Знайти: S -? 3..Дано: (а n )   а4 = 2,4 ; а7 = 6. Знайти: d - ? 4..Дано: (b n )  bп > 0,  b2 = 4,  b4 = 9. Знайти : b3 – ? 5..Дано: (а n )  а1 = 28, а21 = 4. Знайти : d - ? 6..Дано: (b n )  ,    q = 2. Знайти : b5 – ? 7..Дано: (а n ) an = 3n + 5 Знайти: S10–?

ПІДСУМКИ «Я сьогодні був вражений.....» « Я вже вмію....» « Ще треба навчитися....»

Трохи гумору Один з учнів, викликаний до дошки, має йти від свого місця до дошки по прямій. Перший крок він робить довжиною 1 м, другий ½ м, третій 1/4 м і и т. д. так, що довжина наступного кроку в два рази менша довжини попереднього. Чи дійде учень до дошки, якщо відстань місця учня до дошки по прямій 3 м?

Розв’язок Запишемо послідовність чисел Висновок: не дійде!

Домашня контрольна робота Завдання середнього рівня 1. Знайдіть суму нескінченної геометричної прогресії: 12; -6; 3. 2. Чому дорівнює сума п'яти перших членів геометричної прогресії, перший член якої b1=6, а знаменник q= 2. 3. Знайдіть перший член арифметичної прогресії, різниця якої дорівнює 15, а сума її перших тринадцяти членів дорівнює 1326. Завдання достатнього рівня 1. Знайдіть суму десяти перших членів арифметичної прогре сії (an), якщо a6=46, a14=-43. 2. Знайдіть суму чотирьох перших членів геометричної прогресії (bп), якщо b5=16, b8=1024. Завдання високого рівня 1. Знайдіть суму всіх від'ємних членів арифметичної прогресії: -5,2; -4,8; -4,4; ... . 2. Знайдіть перший член і знаменник геометричної прогре сії (bп), якщо b4-b1=-9, b2+b3+b4=-6.