Презентація на тему:
Прогресії. Види прогресій.

Прогресії. Види прогресій. Габузя Сергія 3Гм ІМФІТО

Прогресії бувають двох видів: Арифметичні прогресії; Геометричні прогресії. А зараз про них детальніше

Перше число прогресії називається початковий елемент і позначається a1. Число, на яке ми змінюємо, називається різницею арифметичної прогресії і позначається d. Арифметична прогресія – це послідовність чисел, в якій кожен член відмінний від попереднього на одне і те саме число.

Приклади арифметичної прогресії 1) 1, 3, 5, 7, 9, 11… а1=1, d=2, 2) -12, -8, -4, 0, 4… а1= 3) 3, 3, 3, 3, 3, 3… а1= -12, d= 4, 3, d= 0.

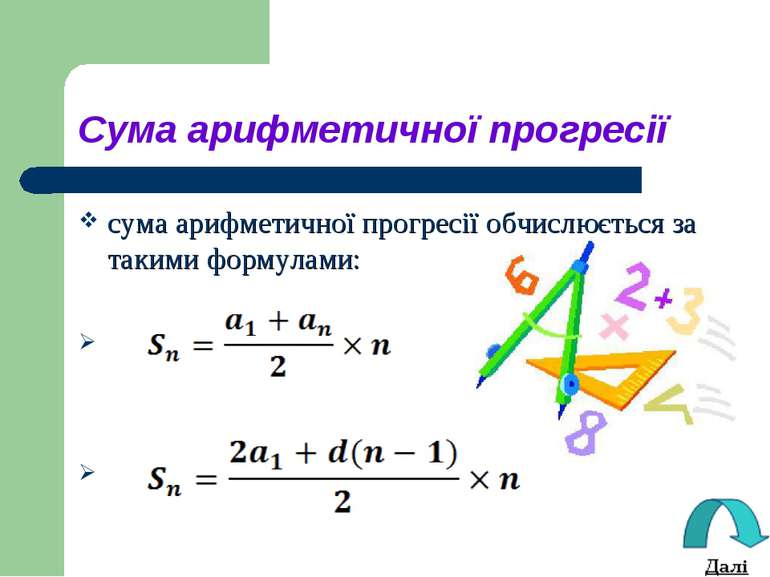
Основні формули арифметичної прогресії формула знаходження n–го елемента арифметичної прогресії - an: an = a1 + d(n-1) формула знаходження різниці арифметичної прогресії - d: d = an+1 - an

Сума арифметичної прогресії сума арифметичної прогресії обчислюється за такими формулами:

Практичні завдання Які з наведених послідовностей чисел є арифметичною прогресією? Перший робітник отримав 20 гривень і кожний наступний з робітників отримував на 5 гривень більше. Скільки заплатили 8 робітникам? а) 15, 17, 21, 23, 25 в) 3, 6, 8, 10, 12 б) 8, 9, 11, 13, 15 г) 10, 12, 14, 16, 18 а) 320 грн. б) 300грн. в) 290грн.

Геометрична прогресія - це послідовність кожен член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Перше число прогресії називається початковий елемент і позначається b1. Число, на яке ми змінюємо, називається знаменник геометричної прогресії – q.

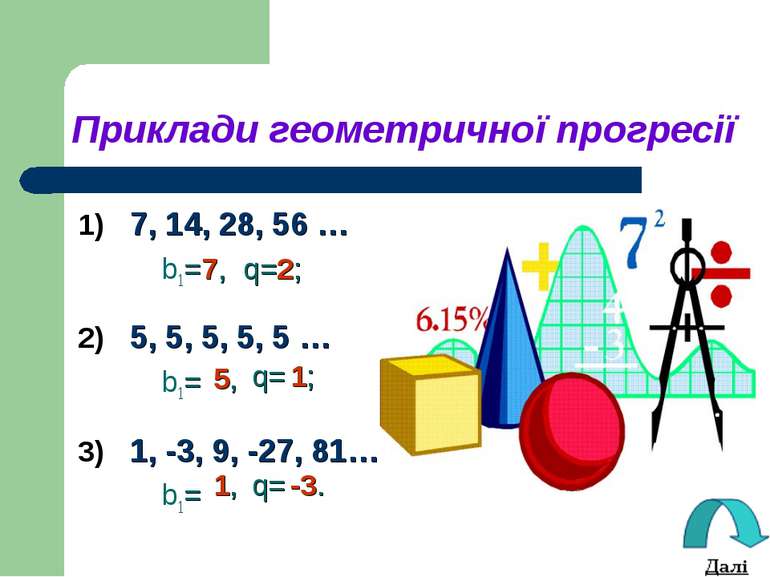
Приклади геометpичної прогресії 1) 7, 14, 28, 56 … b1=7, q=2; 2) 5, 5, 5, 5, 5 … b1= 3) 1, -3, 9, -27, 81… b1= 5, q= 1; 1, -3. q=

Основні формули геометричної прогресії формула знаходження n–го елемента геометричної прогресії - bn: формула знаходження знаменника геометричної прогресії - q:

Види геометричної прогресії Геометрична прогресія буває 3 видів: зростаюча - |q| > 1; стала - |q| = 1; спадна - |q| < 1; Основна властивість геометричної прогресії: (Середнє геометричне)

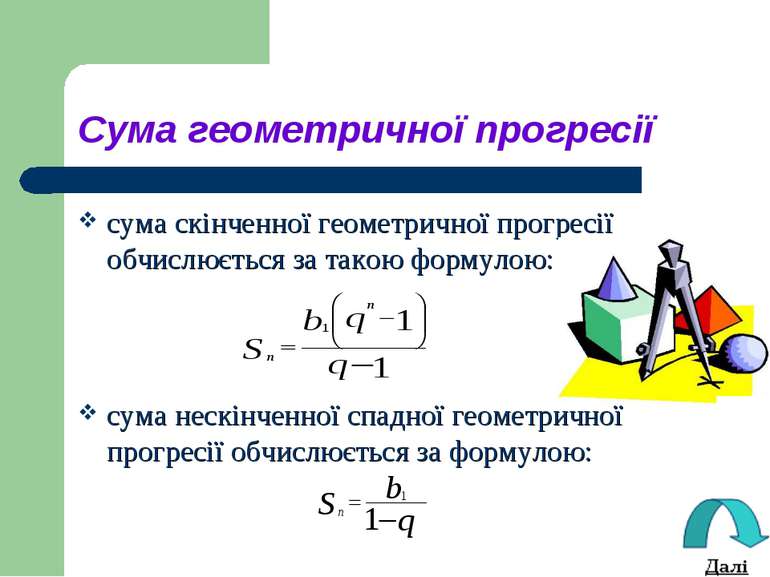
Сума геометричної прогресії сума скінченної геометричної прогресії обчислюється за такою формулою: сума нескінченної спадної геометричної прогресії обчислюється за формулою:

Практичні завдання Які з наведених послідовностей чисел є геометричною прогресією? Знайдіть четвертий член геометричної прогресії, перший член якої b1= 1/27 , а q= -3. г) -3 а) 1, 2, 4, 8, 10 в) 4, 8, 16, 32, 64 б) 2, -10, 50, 100, 150 г) 80, 40, 20, 5, 1 а) -1 б) 1 в) 3

Домашнє завдання Початковий елемент арифметичної прогресії 10. Різниця пргресії – 6. Знайти суму перших 8 членів прогресії. Знайти початковий елемент скінченної геометричної прогресії, якщо її знаменник 3, а сума 5 елементів прогресії дорівнює 242.