Презентація на тему:
Правильний многокутник

ПРАВИЛЬНИЙ МНОГОКУТНИК

МЕТА УРОКУ: Формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв'язування задач

ПРИГАДАЙМО! Сформулюйте означення многокутника; вершин многокутни ка; сторін многокутника; діагоналей многокутника. Які многокутники вам відомі? Скільки утворюється трикутників, якщо в п-кутнику (п > 3) провести всі його діагоналі з однієї вершини? Що таке кут многокутника? зовнішній кут многокутника? Чому дорівнює сума кутів опуклого п-кутника? Чому дорівнює сума зовнішніх кутів опуклого многокутника? В опуклого многокутника всі зовнішні кути прямі. Який це многокутник? Чи можна побудувати чотирикутник з двома прямими і двома тупими кутами? Чи може найменший кут чотирикутника становити 91°? Чи можна побудувати опуклий п'ятикутник, усі кути якого прямі?

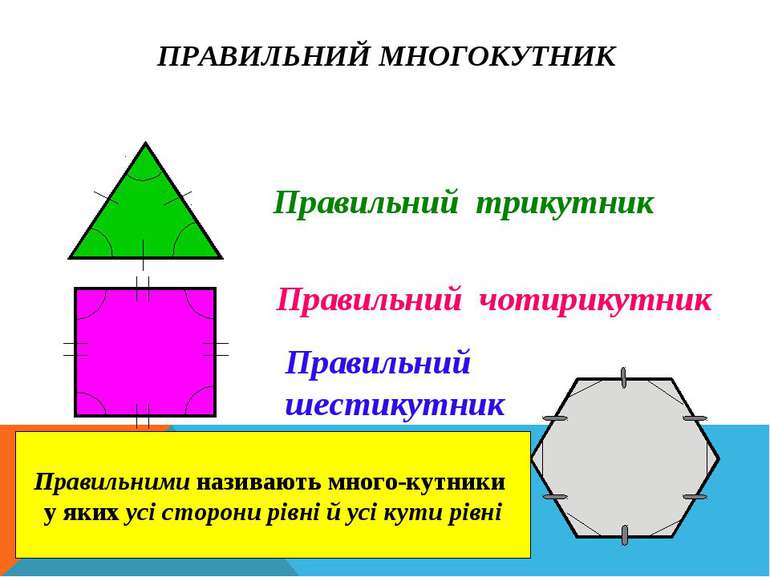
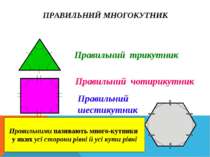
ПРАВИЛЬНИЙ МНОГОКУТНИК Правильний трикутник Правильний чотирикутник Правильний шестикутник Правильними називають много кутники у яких усі сторони рівні й усі кути рівні

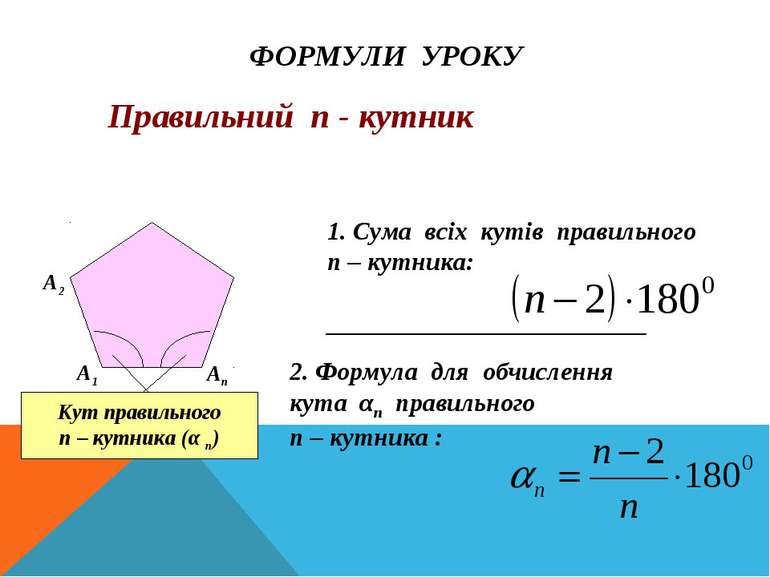
ФОРМУЛИ УРОКУ Кут правильного п – кутника (α п) А1 А2 Ап 1. Сума всіх кутів правильного п – кутника: _________________________ 2. Формула для обчислення кута αп правильного п – кутника : Правильний п - кутник

ТЕСТ Виберіть правильне твердження: 1. Многокутник є правильним, якщо він випуклий і всі його сторони рівні. 2. Будь-який рівносторонній трикутник є правильним. 3. Будь-який чотирикутник з рівними сторонами є правильним.

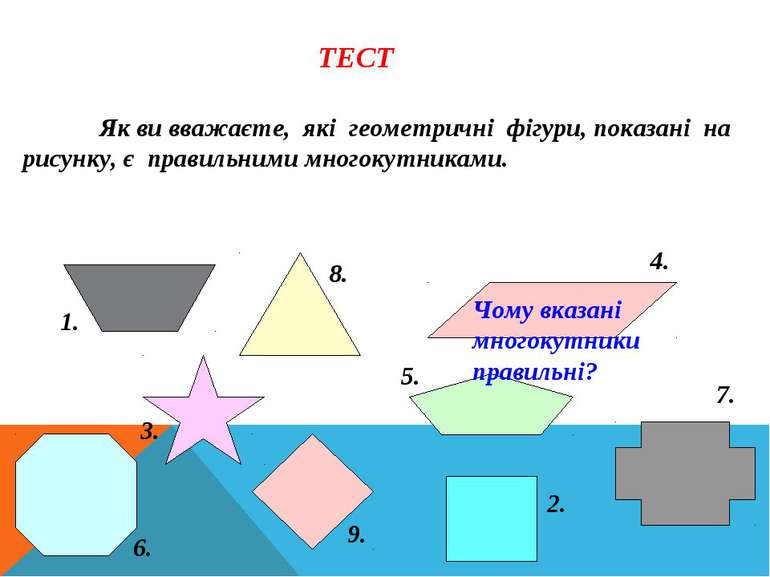
Як ви вважаєте, які геометричні фігури, показані на рисунку, є правильними многокутниками. ТЕСТ 1. 2. 3. 4. 5. 6. 7. 8. 9. Чому вказані многокутники правильні?

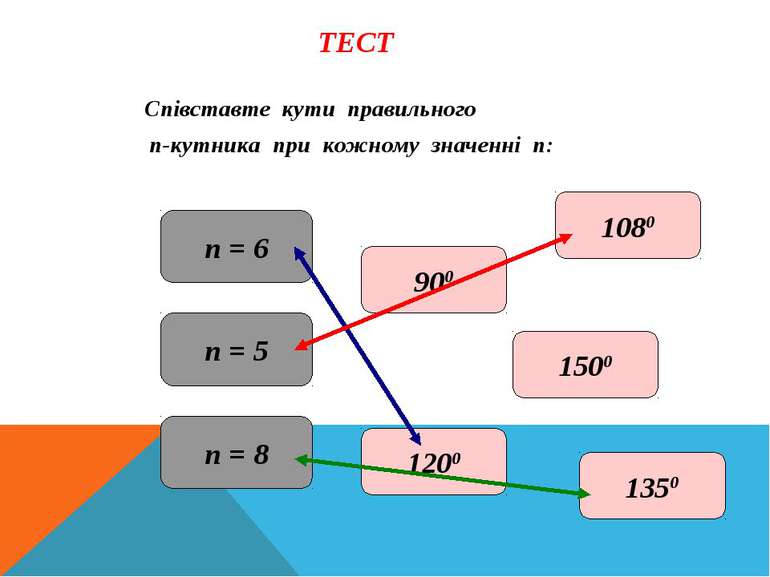
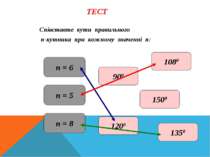
ТЕСТ Співставте кути правильного п-кутника при кожному значенні п: п = 6 п = 5 п = 8 1200 1080 1500 900 1350

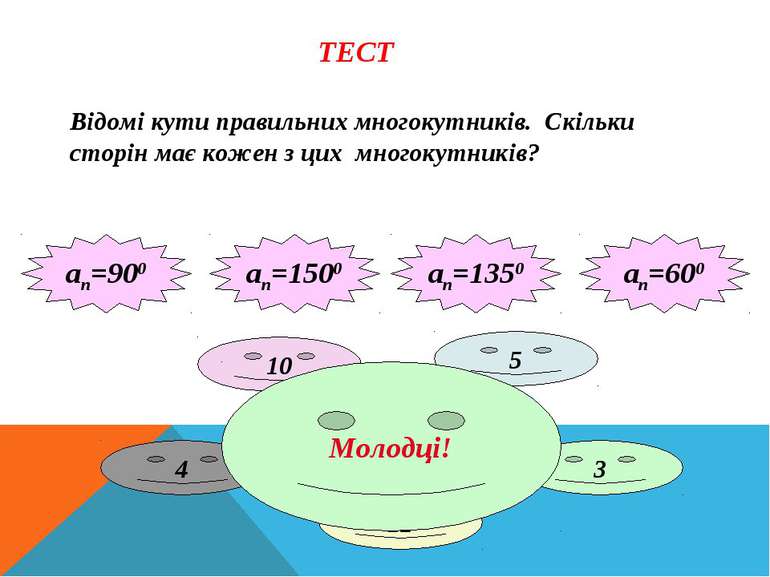
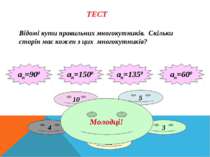
ТЕСТ Відомі кути правильних многокутників. Скільки сторін має кожен з цих многокутників? ап=1350 ап=1500 ап=900 ап=600 4 12 3 8 5 10 Молодці!

ТЕОРЕМА Правильний многокутник є вписаним у коло й описаним навколо кола.

ДОВЕДЕННЯ Нехай А і В — дві сусідні вершини правильного многокутника. Проведемо бісектриси кутів А і В, які пере- тинаються в точці О. Трикутник АОВ — рівнобедрений ( OAB = ОВА = , де α — кут правильного многокутника). Сполучимо точку О з вершиною С, що є сусідньою з вершиною В. ΔАВО = ΔСВО (за першою ознакою рівності трикутників). Із рівності трикутників випливає, що трикутник ОВС — рівнобедрений з кутом C = , тобто CO — бісектриса кута С. Потім сполучимо точку О із вершиною D, що є сусідньою з вершиною С, і доводимо, що трикутник COD — рівнобедрений і DO — бісектриса кута D і т.д. Отже, ΔABO = ΔBCO = ΔCDO = ... Усі ці трикутники мають рівні бічні сторони і рівні висоти, проведені до їхніх основ. Звідси випливає, що всі вершини многокутника лежать на колі з центром О і радіусом, що дорівнює бічним сторонам трикутників, а всі сторони многокутника дотикаються до кола з центром О і радіусом, що дорівнює висотам трикутників, проведеним із вершини О. Теорему доведено.

ЗАДАЧА Доведіть, що взяті через одну вершини правильного 2п-кутника є вершинами правильного п-кутника.

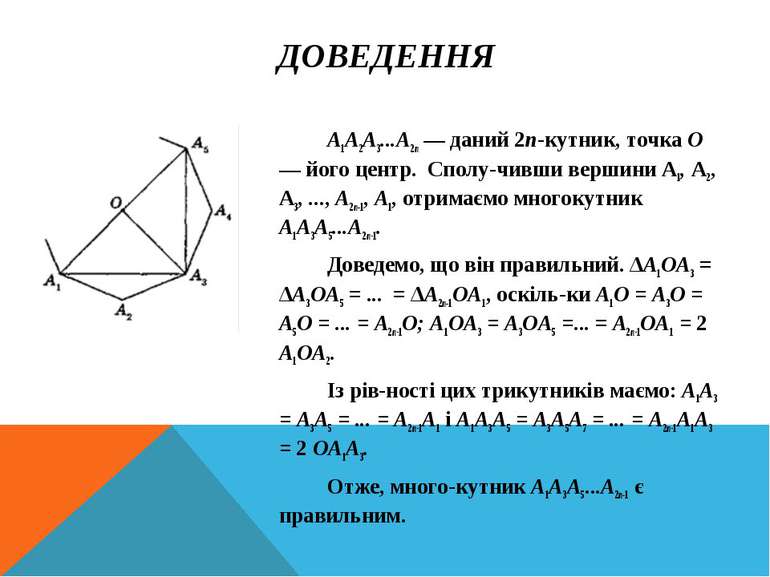
ДОВЕДЕННЯ А1А2А3...А2п — даний 2п-кутник, точка О — його центр. Сполу чивши вершини А1, A2, A3, ..., А2п-1, A1, отримаємо многокутник А1А3А5...А2п-1. Доведемо, що він правильний. ΔA1OA3 = ΔА3ОА5 = ... = ΔA2п-1OA1, оскіль ки А1О = А3О = А5О = ... = А2п-1О; A1ОA3 = A3ОA5 =... = A2n-1OA1 = 2 A1ОA2. Із рів ності цих трикутників маємо: А1А3 = А3А5 = ... = А2п-1А1 і A1A3A5 = A3A5A7 = ... = A2n-1A1A3 = 2 OA1A3. Отже, много кутник A1A3A5...A2п-1 є правильним.

ДОМАШНЄ ЗАВДАННЯ № № № №

ДЖЕРЕЛА: Роганін О.М. Геометрія 9клас: Розробки уроків http://karmanform.ucoz.ru http://ito.vspu.net