Презентація на тему:
Побудова правильних многокутників

Геометрія 9 клас

ознайомлення з правилами побудови правильних многокутників (зокрема трикутників, чотирикутників і шестикутників)

п 3 4 6

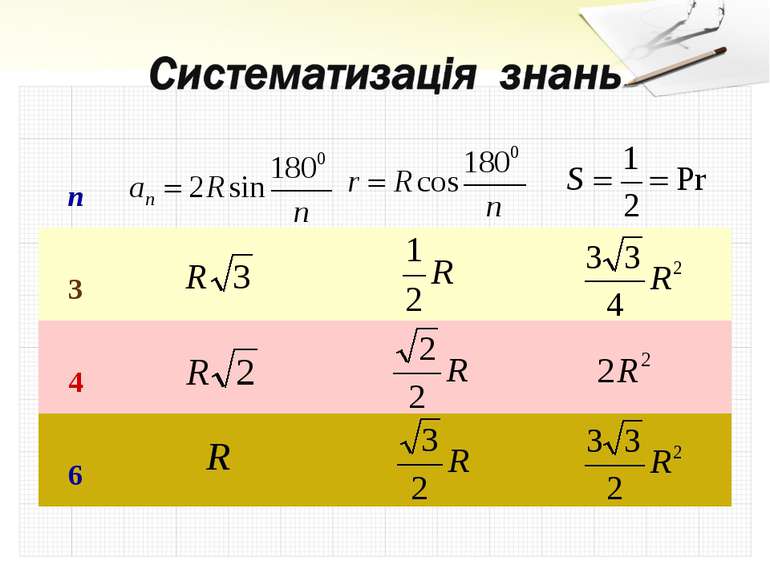
Дано коло, радіус якого дорівнює: Варіант 1 Варіант 2 6 см 8 см Знайдіть: а) сторону правильного трикутника, вписаного в це коло; б) сторону правильного трикутника, описаного навколо цьо го кола; в) сторону правильного чотирикутника, описаного навколо даного кола; г) сторону правильного чотирикутника, вписаного в дане коло; д) сторону правильного шестикутника, вписаного в дане коло; є) периметр правильного шестикутника, описаного навколо цього кола

Варіант 1. а) 6 см; б) 12 см; в) 12 см; г) 6 см; д) 6 см; є) 24 см. Варіант 2. а) 8 см; б) 16 см; в) 16 см; г) 8 см; д) 8 см; є) 32 см.

Карл Гаус, учень першого курсу Геттингенського університету, розв’язав задачу, перед якою математична наука пасувала більше двох тисяч років.

Незважаючи на те, що ще древніми греками були знайдені способи побудови з допомогою тільки циркуля та лінійки правильних многокутників з числом сторін 3, 4, 5, 15, а також з числом сторін, більшим в 2 рази, по відношенню до решти правильних многокутників панувала повна невідомість. И ось в 1796 році майбутній «король математиків» Гаус здогадався, як побудувати правильний 17-кутник, до речі, також, з допомогою циркуля і лінійки. Це відкриття стало поворотним пунктом в його житті: раніш він коливався між філологією і математикою, тепер він твердо вирішив присвятити себе останній. До речі, він заповідав зобразити 17-кутник на своїй надгробній плиті – що й було зроблено.

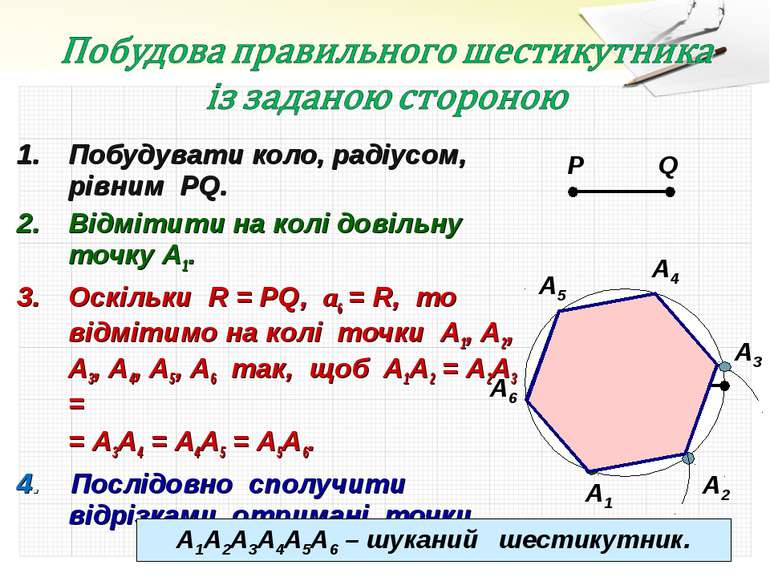
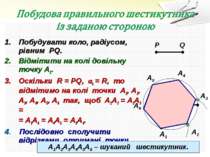
Побудувати коло, радіусом, рівним PQ. Відмітити на колі довільну точку А1. Оскільки R = PQ, а6 = R, то відмітимо на колі точки А1, А2, А3, А4, А5, А6 так, щоб А1А2 = А2А3 = = А3А4 = А4А5 = А5А6. 4. Послідовно сполучити відрізками отримані точки. P Q А1 А2 А3 А1А2А3А4А5А6 – шуканий шестикутник. А4 А5 А6

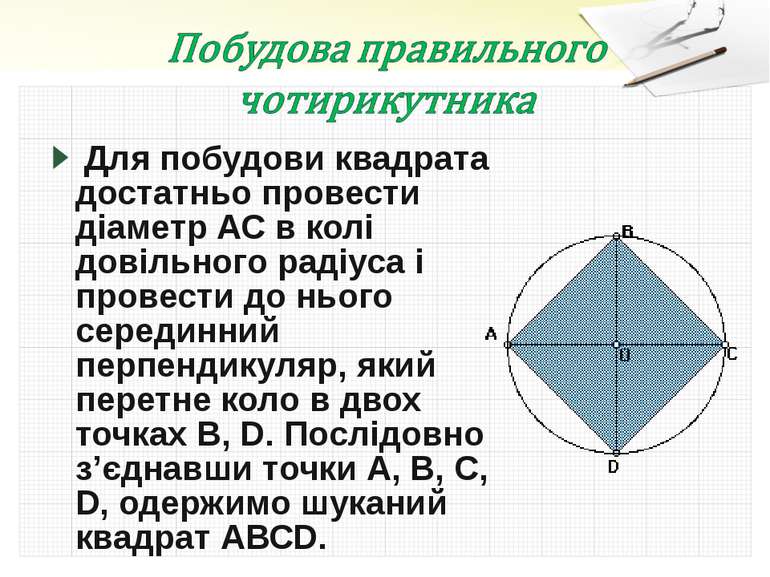
Для побудови квадрата достатньо провести діаметр АС в колі довільного радіуса і провести до нього серединний перпендикуляр, який перетне коло в двох точках В, D. Послідовно з’єднавши точки А, В, С, D, одержимо шуканий квадрат АВСD.

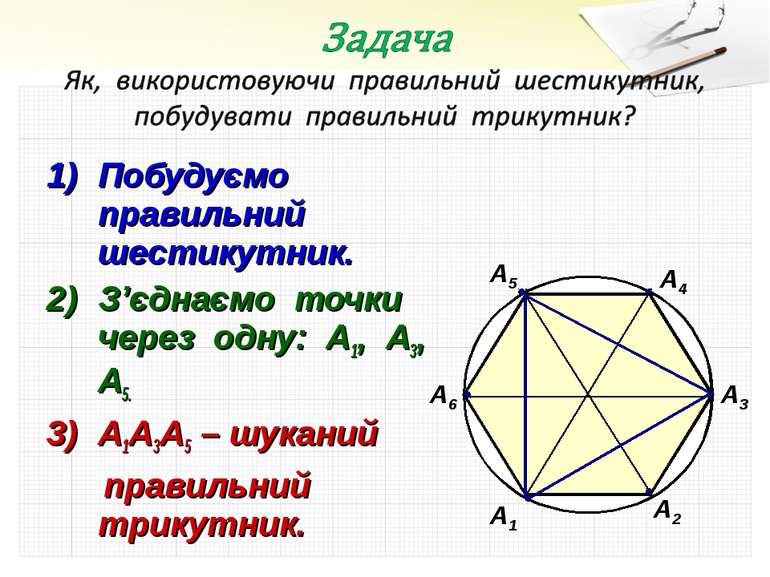
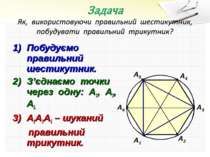
Побудуємо правильний шестикутник. З’єднаємо точки через одну: А1, А3, А5. А1А3А5 – шуканий правильний трикутник. А1 А2 А3 А4 А5 А6

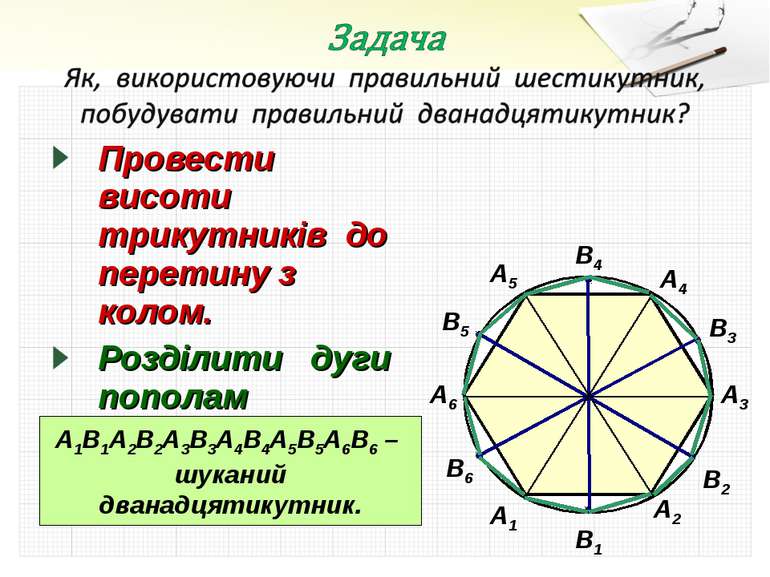
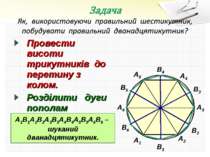
Провести висоти трикутників до перетину з колом. Розділити дуги пополам точками В1, В2, В3, В4, В5, В6. А1 А2 А3 А4 А5 А6 В1 В4 В2 В5 В3 В6 А1В1А2В2А3В3А4В4А5В5А6В6 – шуканий дванадцятикутник.

№ Успіхів!

Роганін О.М. Геометрія 9клас: Розробки уроків http://karmanform.ucoz.ru http://ito.vspu.net