Презентація на тему:
Властивість точки, рівновіддаленої від сторін многокутника

Геометричні місця точок Властивість точки, рівновіддаленої від сторін многокутника Творчий проект Новоренської Мар’яни

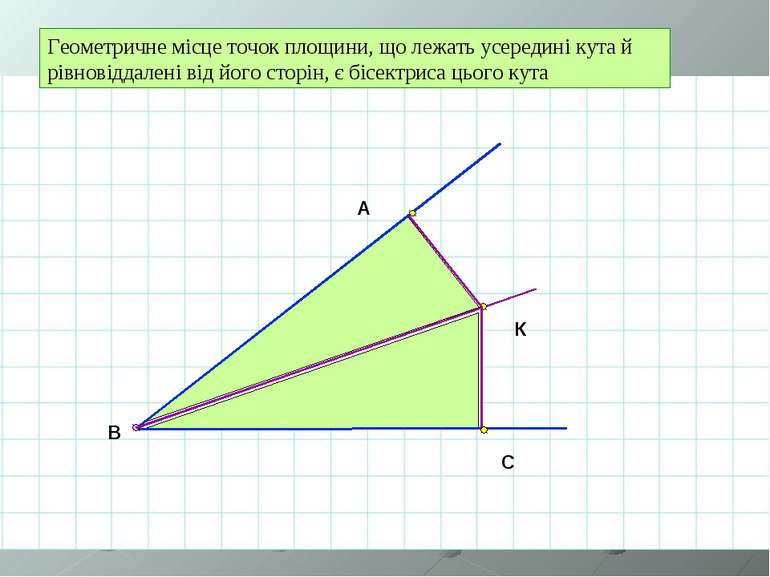
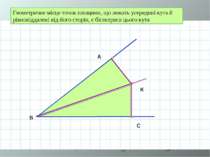
Геометричне місце точок площини, що лежать усередині кута й рівновіддалені від його сторін, є бісектриса цього кута A B C К

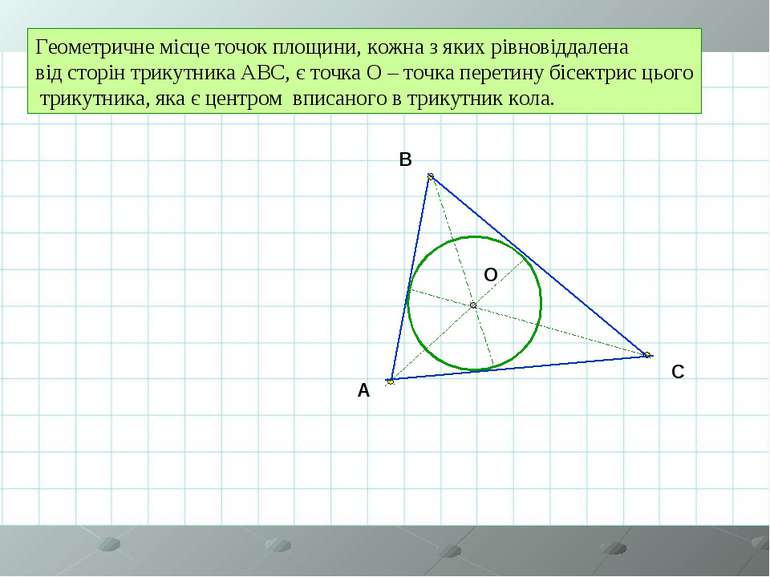
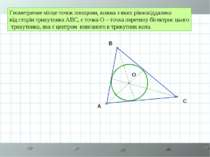
Геометричне місце точок площини, кожна з яких рівновіддалена від сторін трикутника АВС, є точка О – точка перетину бісектрис цього трикутника, яка є центром вписаного в трикутник кола. A B C O

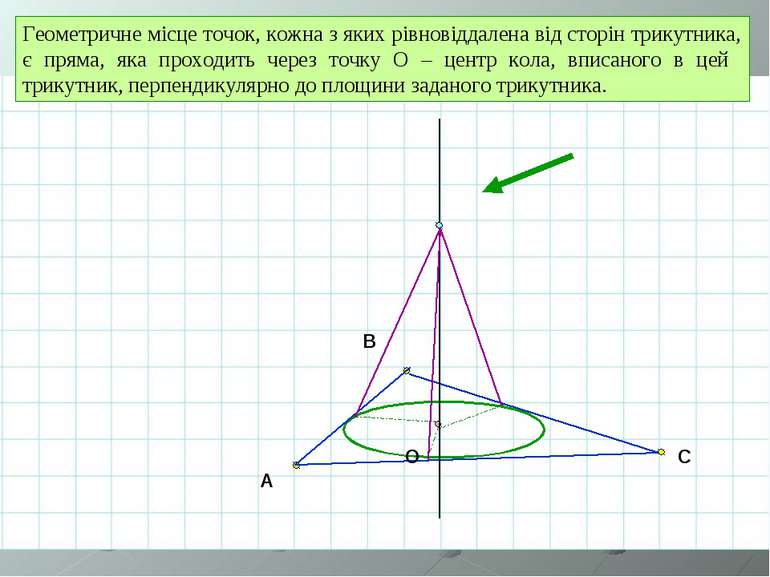
A B C O Геометричне місце точок, кожна з яких рівновіддалена від сторін трикутника, є пряма, яка проходить через точку О – центр кола, вписаного в цей трикутник, перпендикулярно до площини заданого трикутника.

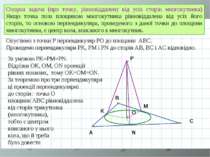
A B C O Опорна задача (про точку, рівновіддалену від усіх сторін многокутника) Якщо точка поза площиною многокутника рівновіддалена від усіх його сторін, то основою перпендикуляра, проведеного з даної точки до площини многокутника, є центр кола, вписаного в многокутник. Р Опустимо з точки Р перпендикуляр РО до площини АВС. Проведемо перпендикуляри PK, PM i PN до сторін АВ, ВС і АС відповідно. N K M За умовою PK=PM=PN. Відрізки ОK, ОM, ОN проекції рівних похилих, тому ОK=ОM=ОN. За теоремою про три перпендикуляри ці проекції перпендикулярні до сторін : точка О площини АВС рівновіддалена від сторін трикутника (многокутника), тобто є центром вписаного у нього кола, що й треба було довести

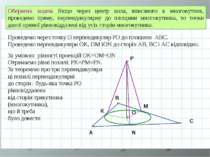
A B C O Р Проведемо через точку О перпендикуляр РО до площини АВС. Проведемо перпендикуляри ОK, ОM iОN до сторін АВ, ВС і АС відповідно. N K M За умовою рівності проекцій ОK=ОM=ОN Отримаємо рівні похилі: PK=PM=PN. За теоремою про три перпендикуляри ці похилі перпендикулярні до сторін : будь-яка точка РО рівновіддалена від сторін трикутника (многокутника), що й треба було довести Обернена задача Якщо через центр кола, вписаного в многокутник, проведено пряму, перпендикулярну до площини многокутника, то точки даної прямої рівновіддалені від усіх сторін многокутника.

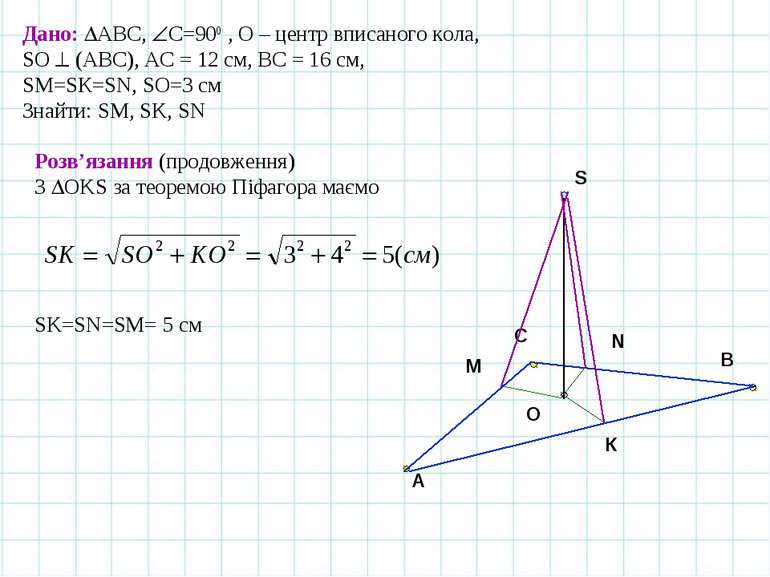
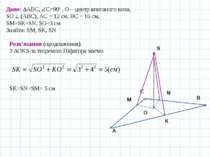
A B C O Задача 1. Катети прямокутного трикутника дорівнюють 12 см і 16см. Точка, рівновіддалена від усіх сторін трикутника, розміщена на відстані 3 см від площини трикутника. Знайдіть відстань від даної точки до сторін трикутника. К Дано: АВС, С=900 , О – центр вписаного кола, SО (АВС), АС = 12 см, ВС = 16 см, SM=SК=SN, SO=3 см Знайти: SM, SK, SN Розв’язання Перпендикуляр SО до площини АВС проектується в центр вписаного кола. З АВС за теоремою Піфагора маємо N M S Для прямокутного трикутника АВС радіус вписаного кола можна обчислити за формулою

A B C O К Дано: АВС, С=900 , О – центр вписаного кола, SО (АВС), АС = 12 см, ВС = 16 см, SM=SК=SN, SO=3 см Знайти: SM, SK, SN Розв’язання (продовження) З OKS за теоремою Піфагора маємо N M S SK=SN=SM= 5 см

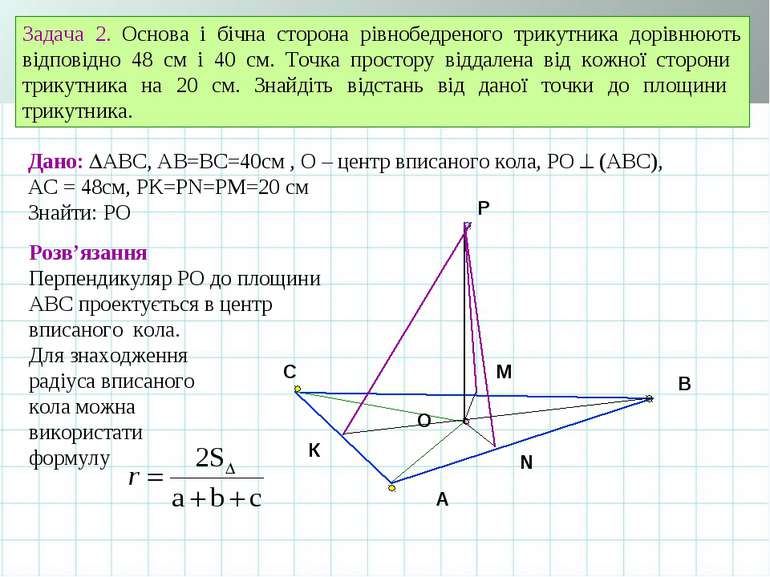
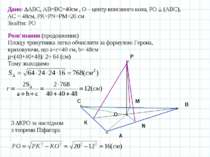
A B C O Задача 2. Основа і бічна сторона рівнобедреного трикутника дорівнюють відповідно 48 см і 40 см. Точка простору віддалена від кожної сторони трикутника на 20 см. Знайдіть відстань від даної точки до площини трикутника. К Дано: АВС, АВ=ВС=40см , О – центр вписаного кола, РО (АВС), АС = 48см, РK=РN=РM=20 см Знайти: РO Розв’язання Перпендикуляр РО до площини АВС проектується в центр вписаного кола. Для знаходження радіуса вписаного кола можна використати формулу Р N M

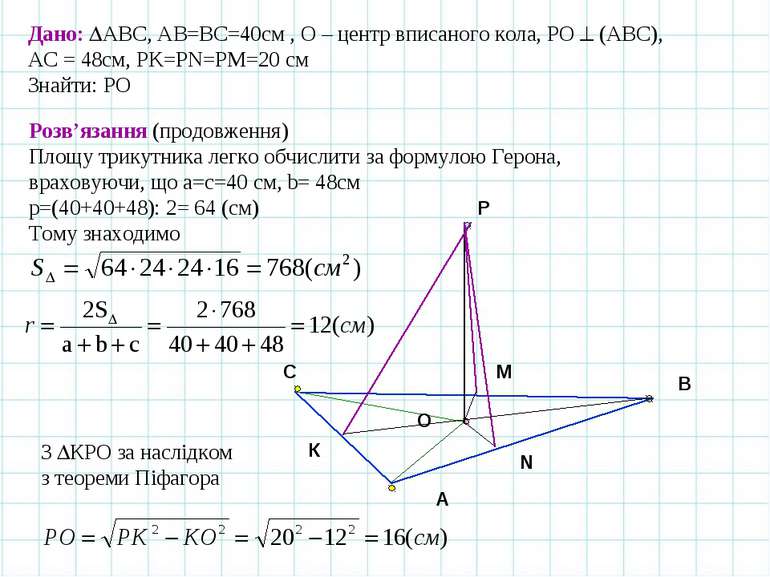
A B C O К Дано: АВС, АВ=ВС=40см , О – центр вписаного кола, РО (АВС), АС = 48см, РK=РN=РM=20 см Знайти: РO Р N M Розв’язання (продовження) Площу трикутника легко обчислити за формулою Герона, враховуючи, що a=c=40 см, b= 48см р=(40+40+48): 2= 64 (см) Тому знаходимо З КРО за наслідком з теореми Піфагора