Презентація на тему:
Проеціювання площини. Точки і прямі в площині. Метод перетворення площин.

Лекція 2 Проеціювання площини. Точки і прямі в площині. Метод перетворення площин. Кафедра нарисної геометрії, інженерної та комп'ютерної графіки

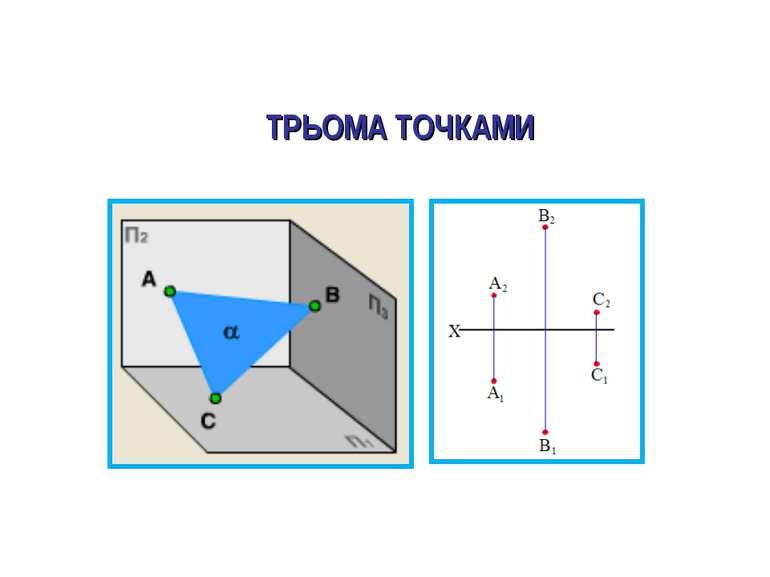
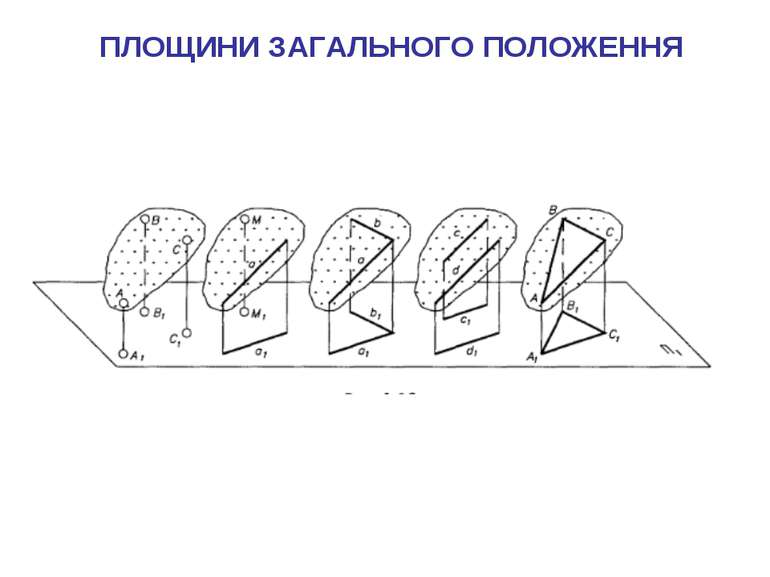
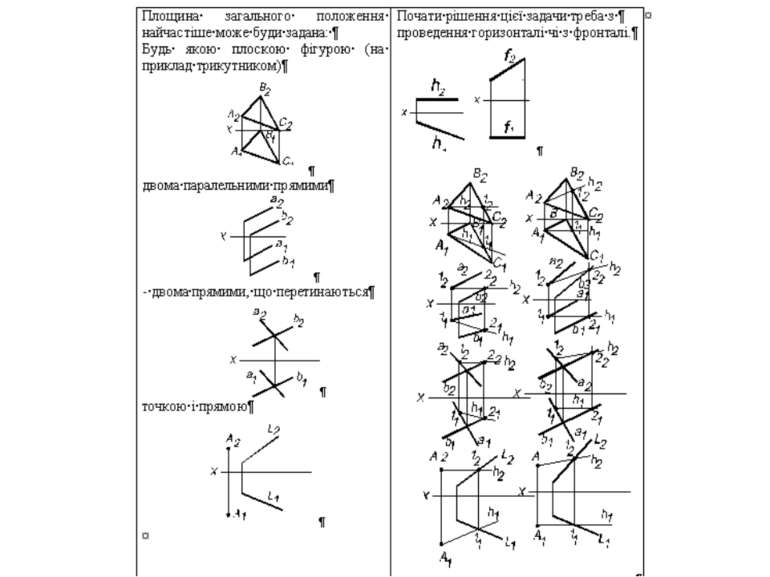
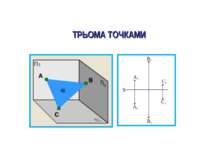
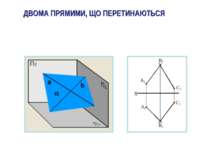
СПОСОБИ ЗАВДАННЯ ПЛОЩИН НА КРЕСЛЕНИКУ Для графічного завдання площини досить задати проекції трьох ії точок, які не належать одній прямій.

ТРЬОМА ТОЧКАМИ

ВІДРІЗКОМ ПРЯМОЇ І ТОЧОЮ

ДВОМА ПРЯМИМИ, ЩО ПЕРЕТИНАЮТЬСЯ

ДВОМА ПАРАЛЕЛЬНИМИ ПРЯМИМИ

ПЛОЩИНИ ЗАГАЛЬНОГО ПОЛОЖЕННЯ

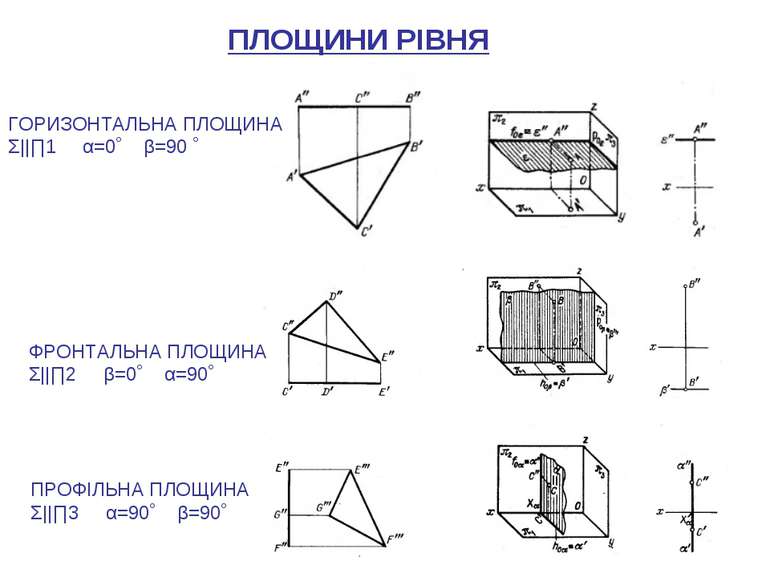
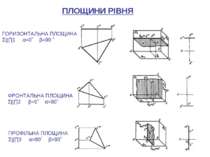
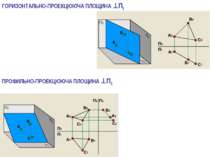
ПЛОЩИНИ РІВНЯ ГОРИЗОНТАЛЬНА ПЛОЩИНА Σ||∏1 α=0˚ β=90 ˚ ФРОНТАЛЬНА ПЛОЩИНА Σ||∏2 β=0˚ α=90˚ ПРОФІЛЬНА ПЛОЩИНА Σ||∏3 α=90˚ β=90˚

ФРОНТАЛЬНО-ПРОЕКЦЮЮЧА ПЛОЩИНА ABC П2

ГОРИЗОНТАЛЬНО-ПРОЕКЦЮЮЧА ПЛОЩИНА П1 ПРОФИЛЬНО-ПРОЕКЦЮЮЧА ПЛОЩИНА П3

Задача: Площина загального положення задана плоскою фігурою – трикутником. Знайти натуральну величину трикутника за допомогою метода заміни площин проекцій. Щоб знайти натуральну величину площини загального положення, треба перетворити ії у площину рівня. Для цього треба виконати дві заміни. Увага ! На всі поставлені питання треба обов’язково дати відповідь. Якщо відповідь дати складно, питання треба запам’ятати чи записати і обов’язково запитати у викладача.

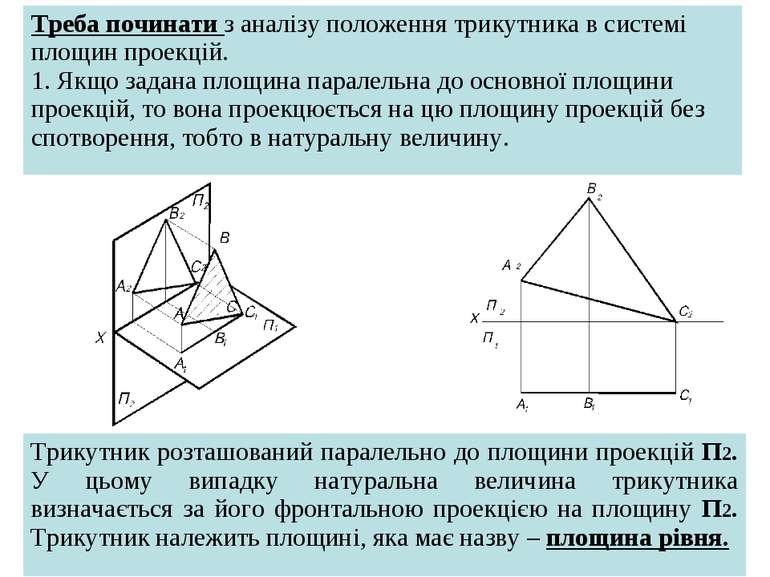
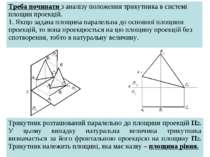
Треба починати з аналізу положення трикутника в системі площин проекцій. 1. Якщо задана площина паралельна до основної площини проекцій, то вона проекцюється на цю площину проекцій без спотворення, тобто в натуральну величину. Трикутник розташований паралельно до площини проекцій П2. У цьому випадку натуральна величина трикутника визначається за його фронтальною проекцією на площину П2. Трикутник належить площині, яка має назву – площина рівня.

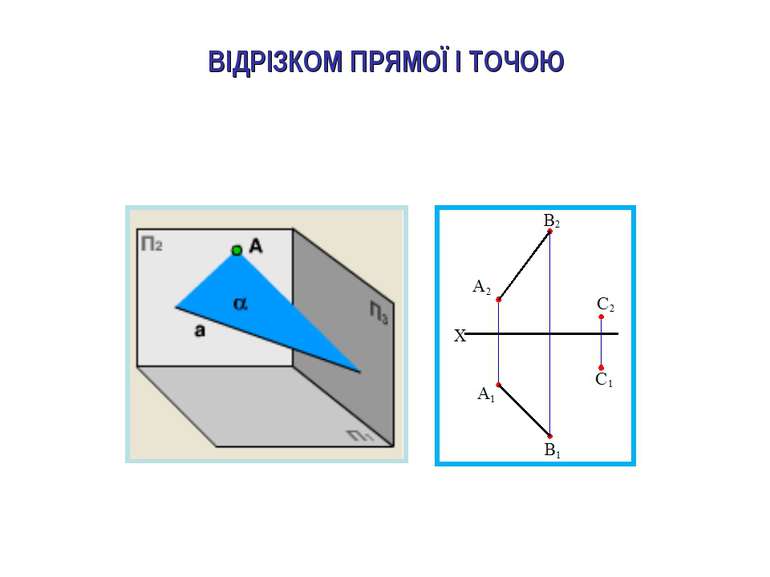
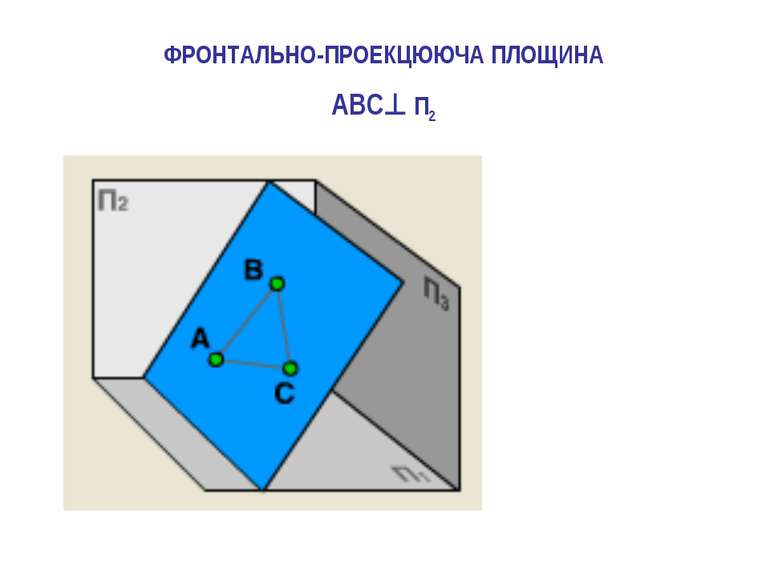
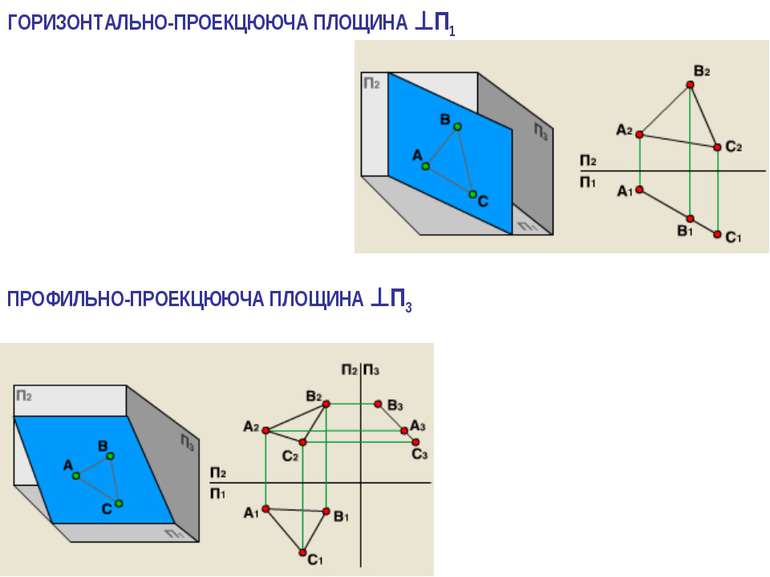
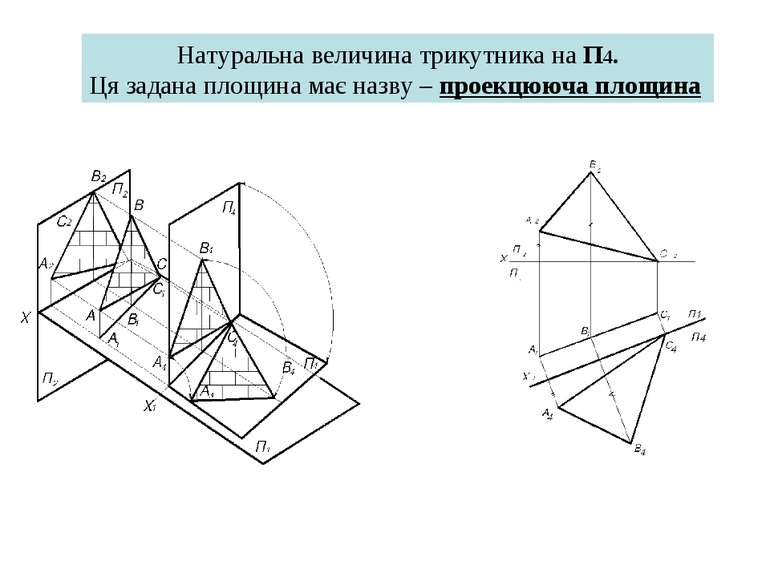
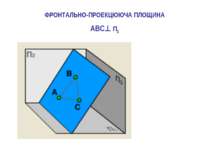
2.Якщо площина трикутника перпендикулярна до площини проекцій, то вона проекцюється на цю площину проекцій у вигляді прямої лінії – сліду проекції, а на іншу площину проекції спотворено. У цьому разі треба зробити одну заміну площин проекцій, щоб знайти натуральну величину заданої плоскої фігури. ЯК ? – паралельно до площини заданої плоскої фігури розташувати нову площину проекцій П4 за умовою, що вона буде перпендикулярна до тієї площини проекцій, що залишається в системі площин проекцій (тобто, або площини П1 чи площини П2).

Натуральна величина трикутника на П4. Ця задана площина має назву – проекцююча площина

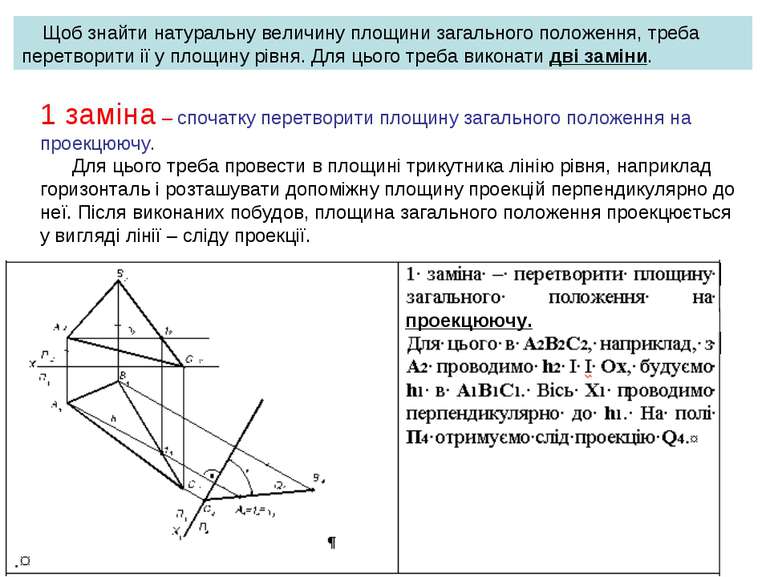
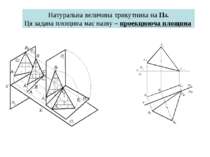
1 заміна – спочатку перетворити площину загального положення на проекцюючу. Для цього треба провести в площині трикутника лінію рівня, наприклад горизонталь і розташувати допоміжну площину проекцій перпендикулярно до неї. Після виконаних побудов, площина загального положення проекцюється у вигляді лінії – сліду проекції. Щоб знайти натуральну величину площини загального положення, треба перетворити ії у площину рівня. Для цього треба виконати дві заміни. проекцюючу.

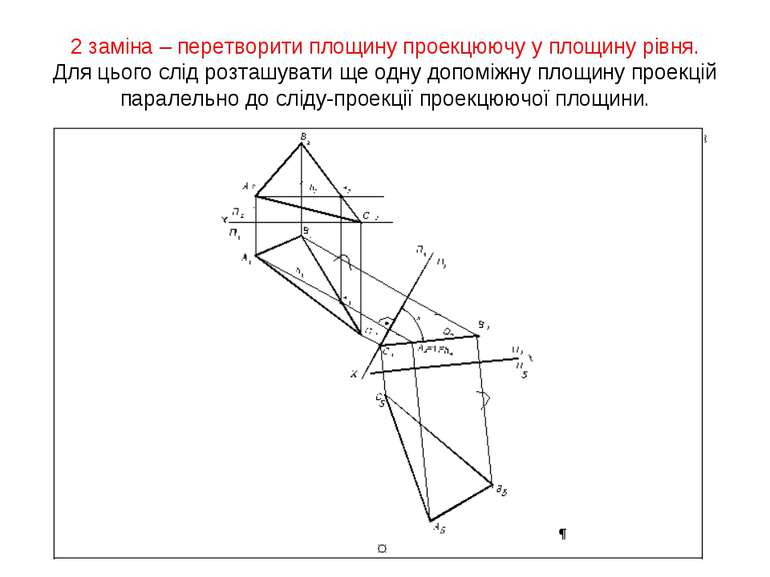
2 заміна – перетворити площину проекцюючу у площину рівня. Для цього слід розташувати ще одну допоміжну площину проекцій паралельно до сліду-проекції проекцюючої площини.

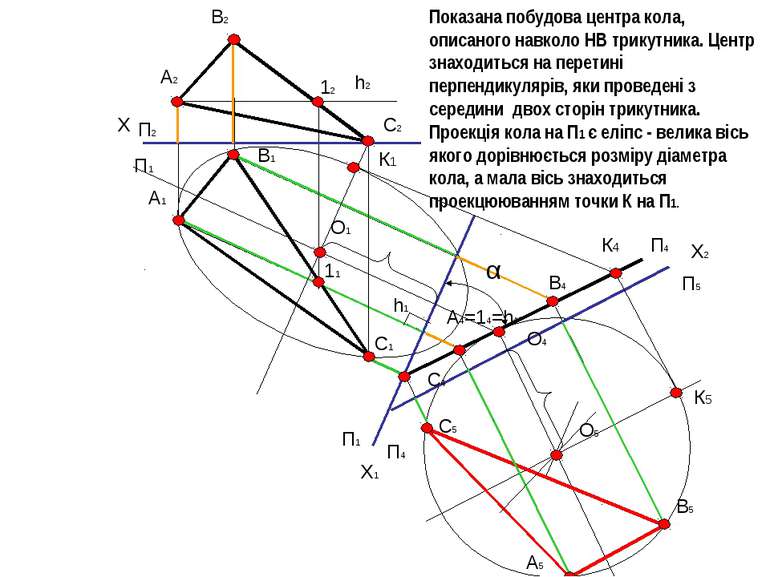
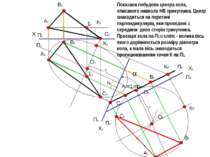
Х П2 П1 А2 А1 В2 В1 С2 С1 12 h2 11 h1 X1 П1 П4 С4 А4=14=h4 B4 X2 П4 П5 А5 В5 С5 O5 O4 O1 α Показана побудова центра кола, описаного навколо НВ трикутника. Центр знаходиться на перетині перпендикулярів, яки проведені з середини двох сторін трикутника. Проекція кола на П1 є еліпс - велика вісь якого дорівнюється розміру діаметра кола, а мала вісь знаходиться проекцююванням точки К на П1. К5 К4 К1

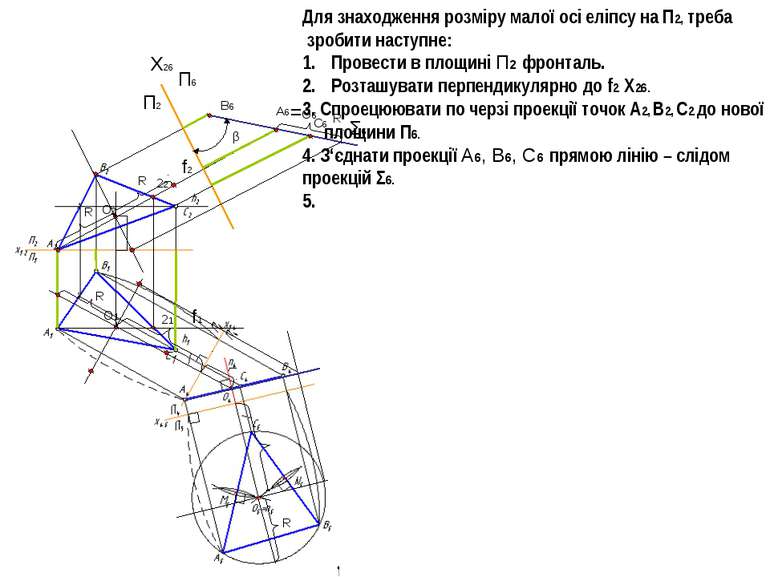
21 22 f1 f2 X26 П2 П6 Σ6 В6 А6 С6 β О1 О2 =О6 R R R R R Для знаходження розміру малої осі еліпсу на П2, треба зробити наступне: Провести в площині П2 фронталь. Розташувати перпендикулярно до f2 Х26. 3. Спроецюювати по черзі проекції точок А2, В2, С2 до нової площини П6. 4. З‘єднати проекції А6, В6, С6 прямою лінію – слідом проекцій Σ6. 5.