Презентація на тему:
Загальне рівняння площини та його дослідження

Загальне рівняння площини та його дослідження Виконали: Степанова Юлія, Фісенко Яна.

Покажемо, що алгебраїчною поверхнею першого порядку є площина. Для цього доведемо такі теореми.

Теорема 1. Площина в прямокутній Декартові системі координат визначається загальним рівнянням першого степеня відносно поточних координат. Доведення. Геометрично будь-яку площину в просторі хуz можна задати за допомогою вектора , перпендикуляр ного до цієї площини, і точки M0 (x0, y0, z0) Через яку проходить дана площина. Візьмемо довільну точку M (х, у, z) і знайдемо вектор . Точка M належить заданій площині тоді і тільки тоді, коли Тоді ;

Оскільки то скалярний добуток можна записати у вигляді: А(х – х0) + В(у – у0) + C(z – z0) = 0, Або Ах + By + Cz - (Aх0 + Ву0 + Cz0) = 0. (1) Позначивши - (AX0 + Ву0 + Cz0) = D дістанемо загальне алгебраїчне рівняння першого степеня: Ах + By + Cz + D = О,

Отже, будь-яка площина в декартових прямокутних координатах може бути зображена рівнянням першого степеня. Зауважимо, що рівняння Ах + By + Cz - (Aх0 + Ву0 + Cz0) = 0 є рівнянням площини, яка проходить Через точку M0 (х0, у0, z0) перпендикулярно до вектора = (А, В, С). Доведемо тепер обернену теорему.

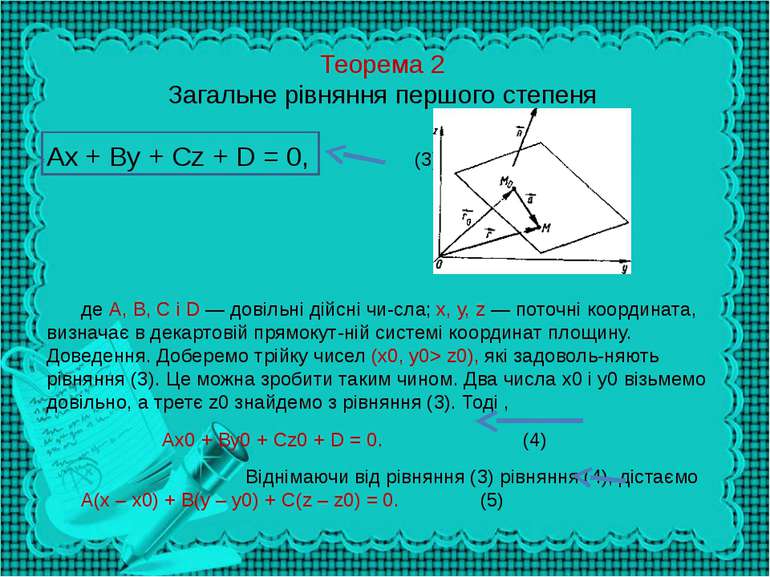
Теорема 2 Загальне рівняння першого степеня Ax + By + Cz + D = 0, (3) де А, В, С і D — довільні дійсні чи сла; х, у, z — поточні координата, визначає в декартовій прямокут ній системі координат площину. Доведення. Доберемо трійку чисел (х0, y0> z0), які задоволь няють рівняння (3). Це можна зробити таким чином. Два числа х0 і у0 візьмемо довільно, а третє z0 знайдемо з рівняння (3). Тоді , Ах0 + Ву0 + Cz0 + D = 0. (4) Віднімаючи від рівняння (3) рівняння (4), дістаємо А(х – х0) + В(у – у0) + C(z – z0) = 0. (5)

Це рівняння є рівнянням площини, перпендикулярної до векто ра = (А, В, С) і такої, що проходить через точку M0 (х0, у0, z0). Таким чином, кожна площина є поверхнею першого порядку, і, навпаки, кожна поверхня першого порядку є площиною. Тому рівняння (l) або (3) називається загальним рівнянням площини. Рівняння ; =0 (6) називається векторним рівнянням площини. Враховуючи, що векторне рівняння площини запишемо у вигляді: , або Якщо у загальному рівнянні площини покласти z – z0 = 0, то дістанемо рівняння, А(х – х0) + В(у – у0) = 0, або Ах + By + С = 0, (7) де С = - (Ax0 + Ву0). Рівняння ( 7) називається загальним рів нянням прямої, що лежить у площині хОу.

Дослідження загального рівняння площини Розглянемо загальне рівняння площини . Ах + Вy + Cz + D = 0. (8) де А, В, С і D — довільні числа, причому хоча б одне з перших трьох відмінне від нуля.

Дослідимо окремі випадки цього рівняння. 1 випадок Якщо D = О, то рівняння (8) набирає вигляду; Ах + By + Cz = 0 (9) Це рівняння задовольняє точка О (0, 0, 0). Отже, рівняння (9) визначає площину, яка проходить через початок координат.

2 випадок Якщо А = 0, то рівняння (8) має вигляд: By + Cz + D = О (10) і визначає площину, нормальний вектор якої = (О, В, С) перпен дикулярний до осі Ох. Отже, рівняння (10) визначає площину, паралельну осі абсцис, або перпендикулярну до площини yOz.

3 випадок Якщо А = В = 0, а С 0, то маємо рівняння площини, паралельної хОу: Рівняння х = 0, у = 0, z = 0 визначають відповідно координатні площини yOz, xOz, хОу.