Презентація на тему:
Властивість точки, рівновіддаленої від вершин многокутника

Геометричні місця точок Властивість точки, рівновіддаленої від вершин многокутника Творчий проект Фотенюк Надії

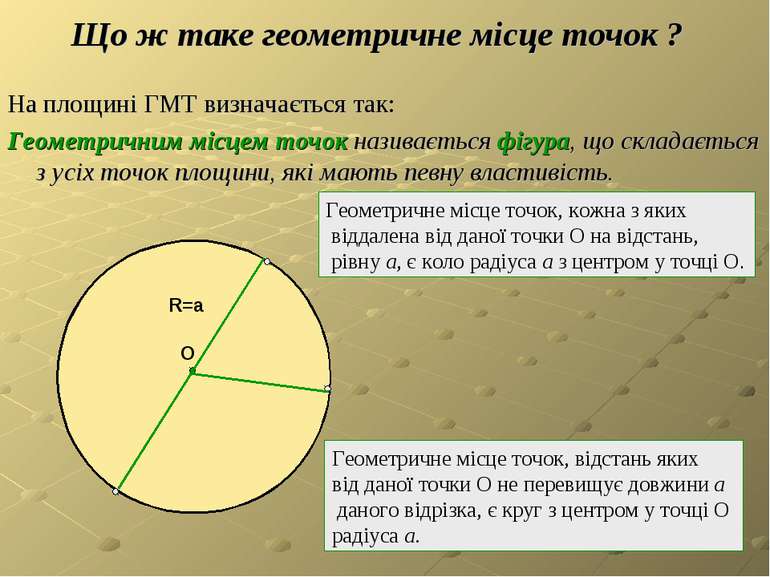
Що ж таке геометричне місце точок ? На площині ГМТ визначається так: Геометричним місцем точок називається фігура, що складається з усіх точок площини, які мають певну властивість. Геометричне місце точок, кожна з яких віддалена від даної точки О на відстань, рівну a, є коло радіуса a з центром у точці О. Геометричне місце точок, відстань яких від даної точки О не перевищує довжини a даного відрізка, є круг з центром у точці О радіуса a. О R=a

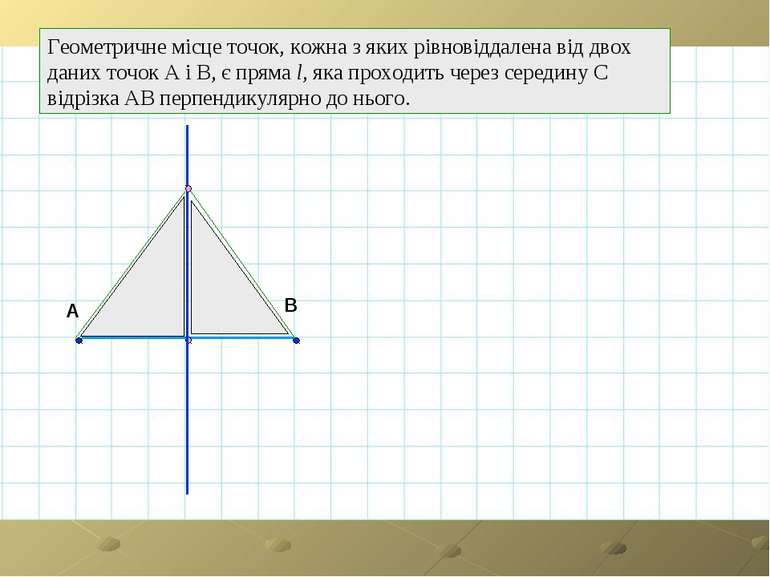
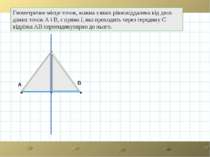
Геометричне місце точок, кожна з яких рівновіддалена від двох даних точок А і В, є пряма l, яка проходить через середину С відрізка АВ перпендикулярно до нього. A B C

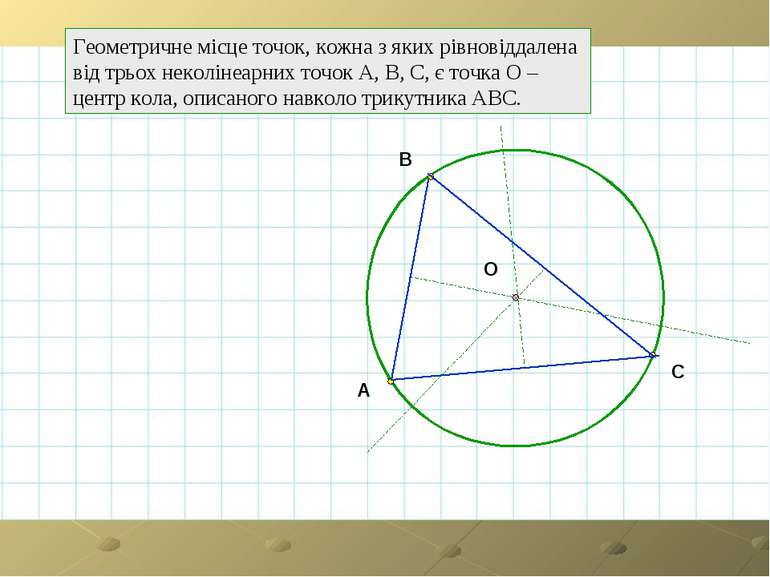
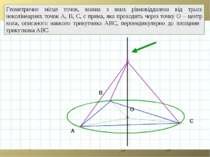
Геометричне місце точок, кожна з яких рівновіддалена від трьох неколінеарних точок А, В, С, є точка О – центр кола, описаного навколо трикутника АВС. A B C O

У просторі ГМТ визначається так: Геометричним місцем точок у просторі називається деяка фігура, що складається з усіх об’єктів простору, положення яких задовольняє одній або кільком певним умовам. О Геометричне місце точок, відстань яких від даної точки О не перевищує довжини a даного відрізка, є куля з центром у точці О радіуса a. Геометричне місце точок, кожна з яких віддалена від даної точки О на відстань, рівну a, є сфера радіуса a з центром у точці О.

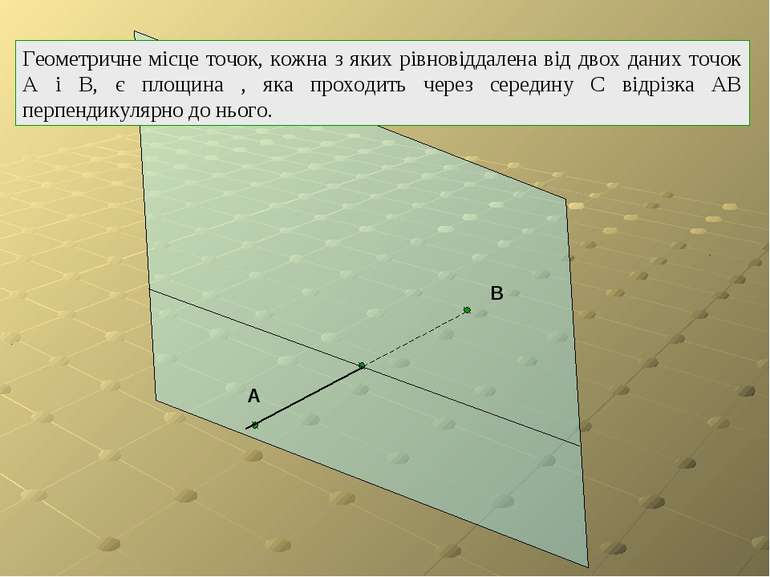
Геометричне місце точок, кожна з яких рівновіддалена від двох даних точок А і В, є площина , яка проходить через середину С відрізка АВ перпендикулярно до нього. A B

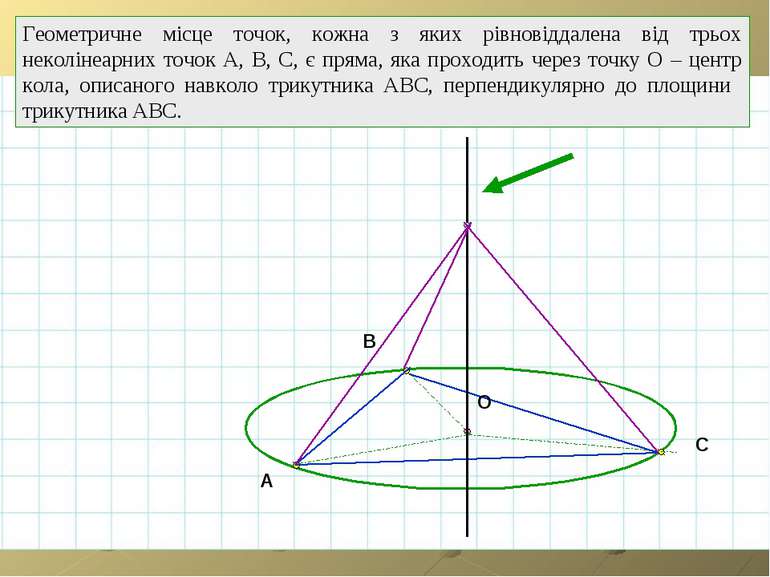
A B C O Геометричне місце точок, кожна з яких рівновіддалена від трьох неколінеарних точок А, В, С, є пряма, яка проходить через точку О – центр кола, описаного навколо трикутника АВС, перпендикулярно до площини трикутника АВС.

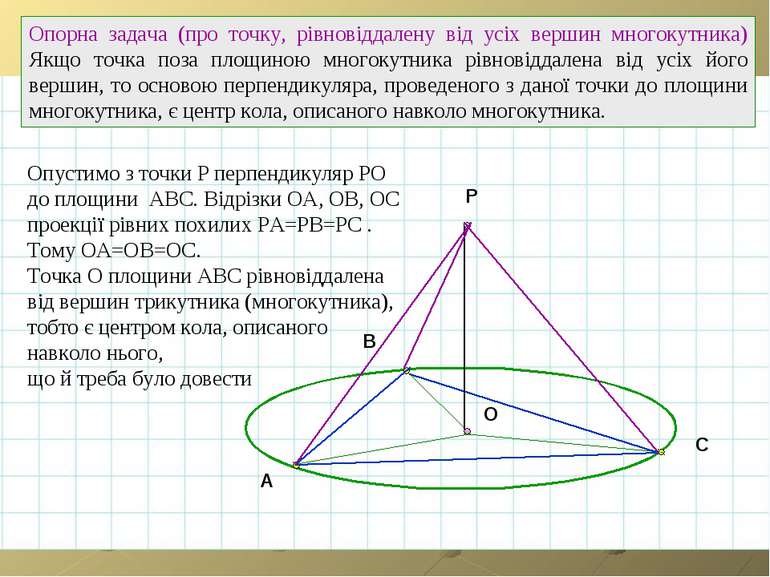
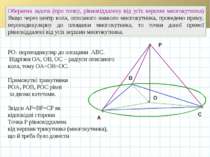
A B C O Опорна задача (про точку, рівновіддалену від усіх вершин многокутника) Якщо точка поза площиною многокутника рівновіддалена від усіх його вершин, то основою перпендикуляра, проведеного з даної точки до площини многокутника, є центр кола, описаного навколо многокутника. Р Опустимо з точки Р перпендикуляр РО до площини АВС. Відрізки ОА, ОВ, ОС проекції рівних похилих РА=РВ=РС . Тому ОА=ОВ=ОС. Точка О площини АВС рівновіддалена від вершин трикутника (многокутника), тобто є центром кола, описаного навколо нього, що й треба було довести

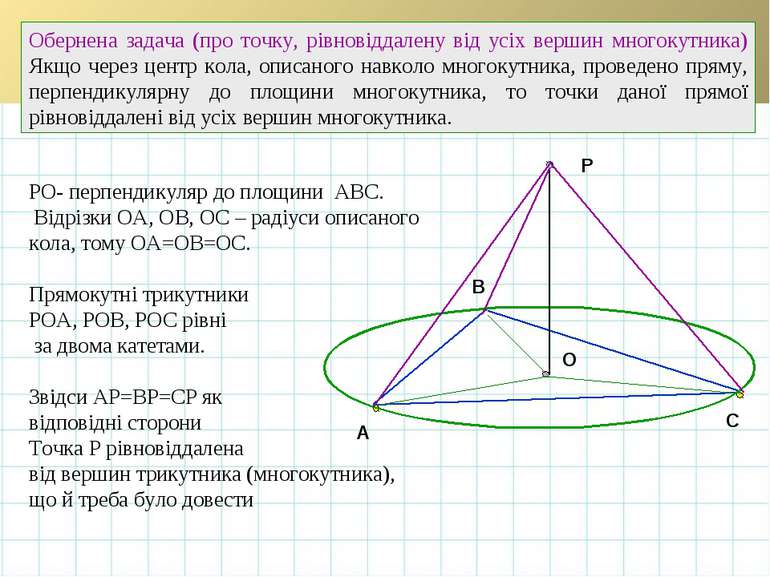
A B C Р O Обернена задача (про точку, рівновіддалену від усіх вершин многокутника) Якщо через центр кола, описаного навколо многокутника, проведено пряму, перпендикулярну до площини многокутника, то точки даної прямої рівновіддалені від усіх вершин многокутника. РО- перпендикуляр до площини АВС. Відрізки ОА, ОВ, ОС – радіуси описаного кола, тому ОА=ОВ=ОС. Прямокутні трикутники РОА, РОВ, РОС рівні за двома катетами. Звідси АР=ВР=СР як відповідні сторони Точка Р рівновіддалена від вершин трикутника (многокутника), що й треба було довести

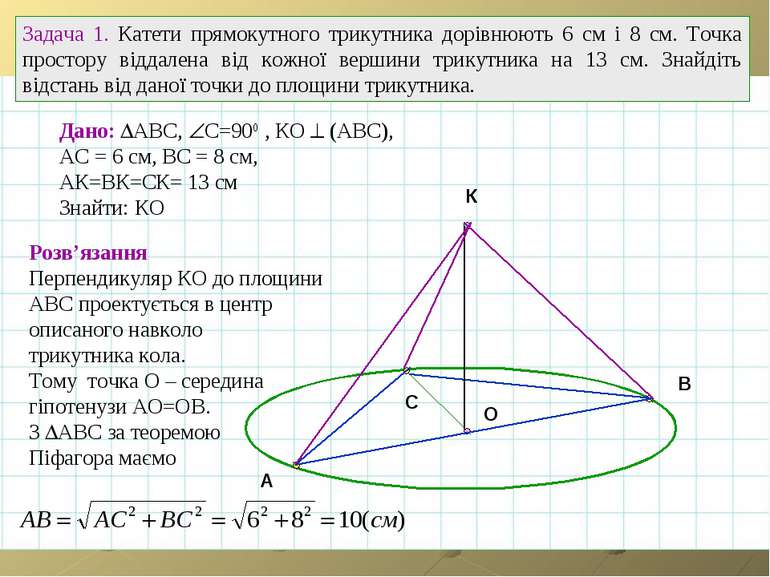
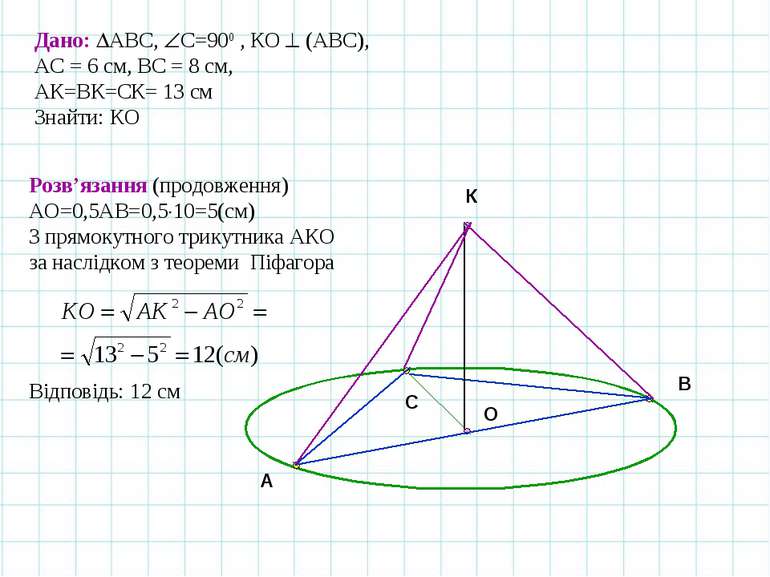
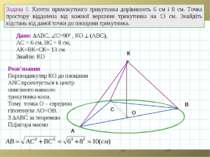
A B C O Задача 1. Катети прямокутного трикутника дорівнюють 6 см і 8 см. Точка простору віддалена від кожної вершини трикутника на 13 см. Знайдіть відстань від даної точки до площини трикутника. К Дано: АВС, С=900 , КО (АВС), АС = 6 см, ВС = 8 см, АК=ВК=СК= 13 см Знайти: КО Розв’язання Перпендикуляр КО до площини АВС проектується в центр описаного навколо трикутника кола. Тому точка О – середина гіпотенузи АО=ОВ. З АВС за теоремою Піфагора маємо

A B C O К Дано: АВС, С=900 , КО (АВС), АС = 6 см, ВС = 8 см, АК=ВК=СК= 13 см Знайти: КО Розв’язання (продовження) АО=0,5АВ=0,5 10=5(см) З прямокутного трикутника АКО за наслідком з теореми Піфагора Відповідь: 12 см

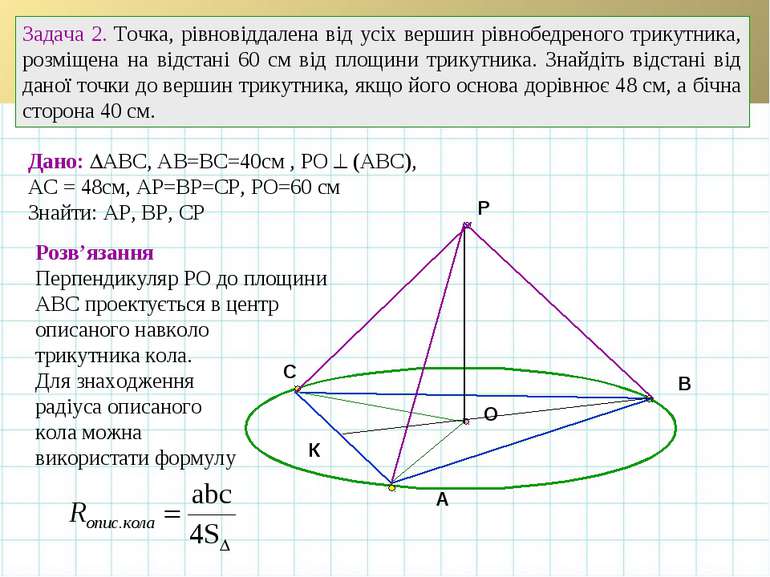
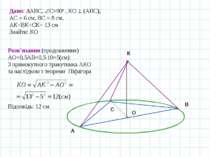
A B C O Задача 2. Точка, рівновіддалена від усіх вершин рівнобедреного трикутника, розміщена на відстані 60 см від площини трикутника. Знайдіть відстані від даної точки до вершин трикутника, якщо його основа дорівнює 48 см, а бічна сторона 40 см. К Дано: АВС, АВ=ВС=40см , РО (АВС), АС = 48см, АР=ВР=СР, РО=60 см Знайти: АР, ВР, СР Розв’язання Перпендикуляр РО до площини АВС проектується в центр описаного навколо трикутника кола. Для знаходження радіуса описаного кола можна використати формулу Р

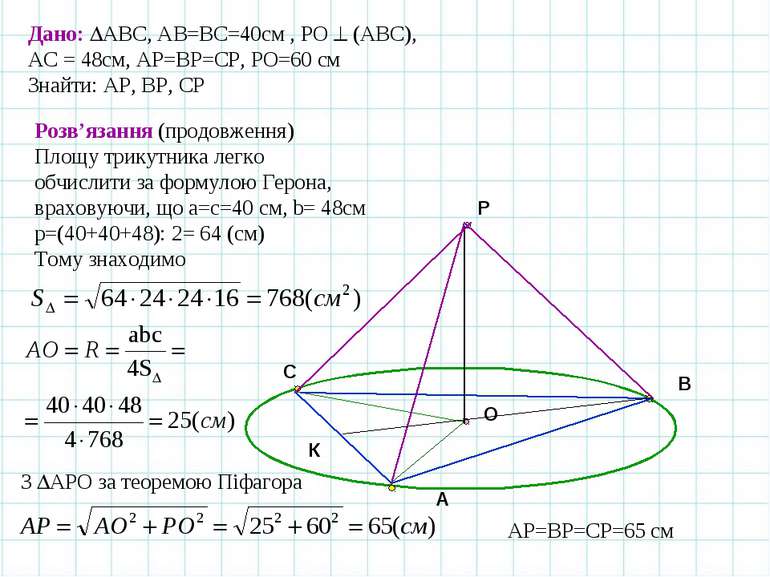
A B C O К Дано: АВС, АВ=ВС=40см , РО (АВС), АС = 48см, АР=ВР=СР, РО=60 см Знайти: АР, ВР, СР Розв’язання (продовження) Площу трикутника легко обчислити за формулою Герона, враховуючи, що a=c=40 см, b= 48см р=(40+40+48): 2= 64 (см) Тому знаходимо Р З АРО за теоремою Піфагора АР=ВР=СР=65 см

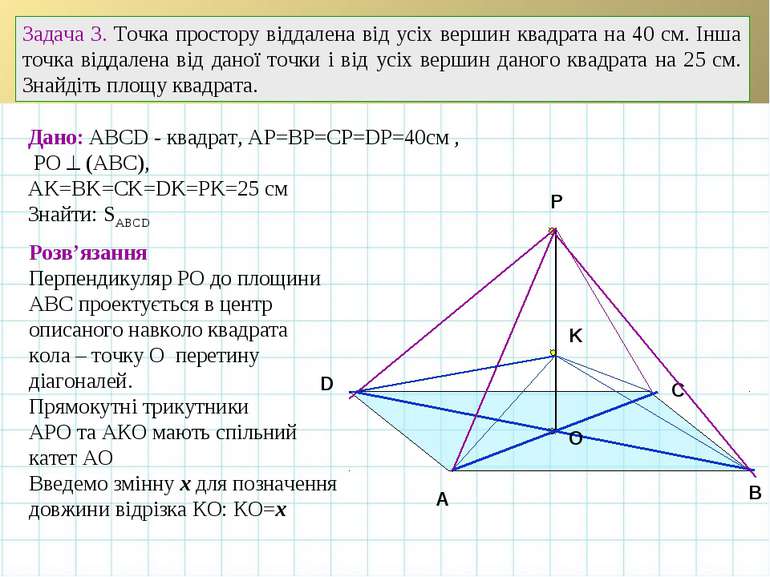
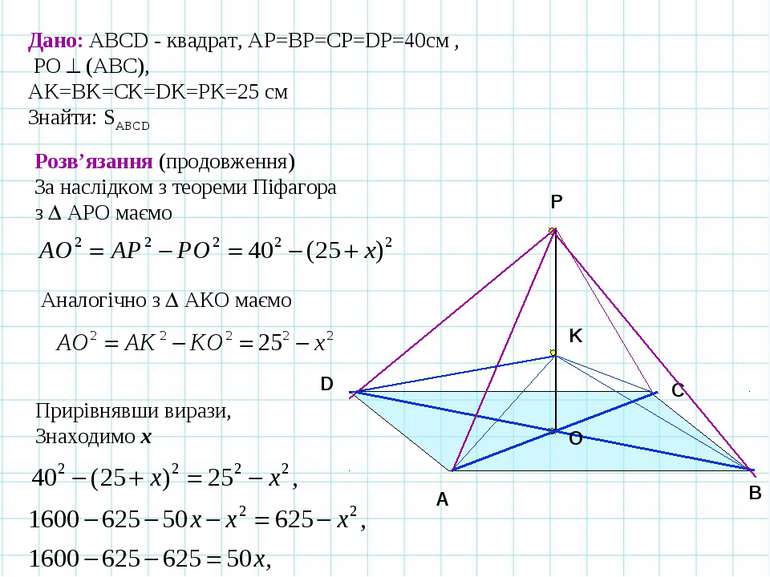
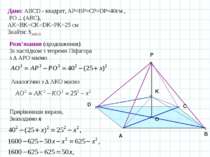
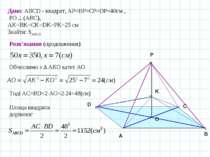
A B C O Задача 3. Точка простору віддалена від усіх вершин квадрата на 40 см. Інша точка віддалена від даної точки і від усіх вершин даного квадрата на 25 см. Знайдіть площу квадрата. D Дано: АВСD - квадрат, АP=ВP=CP=DP=40см , РО (АВС), АK=BK=CK=DK=РK=25 см Знайти: SABCD Розв’язання Перпендикуляр РО до площини АВС проектується в центр описаного навколо квадрата кола – точку О перетину діагоналей. Прямокутні трикутники АРО та АКО мають спільний катет АО Введемо змінну х для позначення довжини відрізка КО: КО=х K Р

A B C O D Дано: АВСD - квадрат, АP=ВP=CP=DP=40см , РО (АВС), АK=BK=CK=DK=РK=25 см Знайти: SABCD Розв’язання (продовження) За наслідком з теореми Піфагора з АРО маємо K Р Аналогічно з АКО маємо Прирівнявши вирази, Знаходимо х

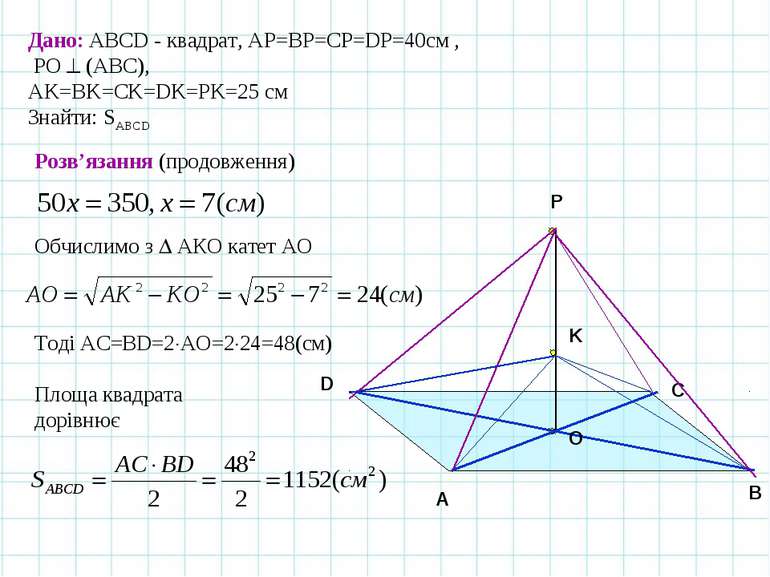
A B C O D Дано: АВСD - квадрат, АP=ВP=CP=DP=40см , РО (АВС), АK=BK=CK=DK=РK=25 см Знайти: SABCD Розв’язання (продовження) K Р Обчислимо з АКО катет АО Тоді АС=BD=2 AO=2 24=48(cм) Площа квадрата дорівнює