Презентація на тему:
Координати та вектори в просторі

Урок узагальнення та систематизації знань з теми “Координати та вектори в просторі”. Контрольна робота Урок математики в 11 класі Рівень стандарту. 2 уроки (пара)

Мета: Узагальнити та систематизувати знання з теми “Координати та вектори в просторі”, провести огляд типових вправ з цієї теми. Перевірити якість засвоєння учнями знань та умінь з теми. Урок з використанням ІКТ технологій. Шполянський НВК “ЗОШ І-ІІІ ст. №3- гімназія” Шполянської районної Ради Черкаської області вчитель математики Любімова Людмила Олексіївна * *

Огляд типових вправ Фронтальна робота. №1 Опишіть будову прямокутної системи координат у просторі. Яку назву мають координатні осі? Чому дорівнюють абсциса і апліката точки, яка знаходиться на осі ординат? Чи правильно, що точка М(3;-2;0) знаходиться в площині xy? x y z o 1

А В №2 За якою формулою знаходять відстань між двома точками у просторі, якщо відомі їх координати? Чому дорівнює відстань між точками А(-1;2;0) і В(-2;-2;3)?

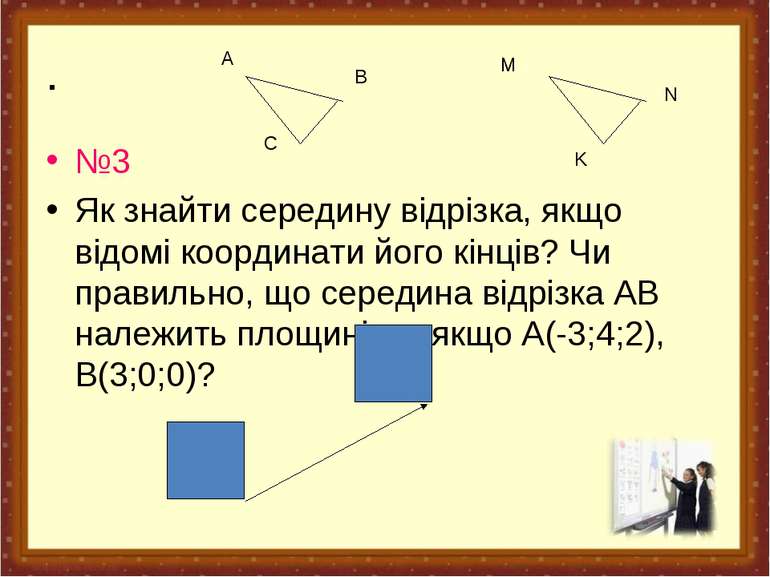
А В №3 Як знайти середину відрізка, якщо відомі координати його кінців? Чи правильно, що середина відрізка АВ належить площині yz, якщо А(-3;4;2), В(3;0;0)?

. №3 Як знайти середину відрізка, якщо відомі координати його кінців? Чи правильно, що середина відрізка АВ належить площині yz, якщо А(-3;4;2), В(3;0;0)? A B C M N K

. №5 Які точки називають симетричними відносно точки? Прямої? Площини? Які фігури називаються симетричними відносно точки? Прямої? Площини? Наведіть приклади таких фігур. О а

. №6 Що називають паралельним перенесенням? Сформулюйте властивості паралельного перенесення. Наведіть формули, які задають паралельне перенесення точки А(x;y;z) у точку А (x ;y ;z ). A A

. №7 Що називають вектором? Як знайти координати вектора, якщо відомі його початок і кінець? Знайдіть координати вектора АВ, якщо А(2;-3;5), В(-1;0;-2). А В

. №8 Як обчислити довжину (модуль) вектора, якщо відомі його координати? Знайдіть довжину вектора а(2;1;-3). a

. №9 Поясніть, як знайти суму й різницю векторів, заданих геометрично та координатами? Знайдіть суму і різницю векторів а(3;1;-3) і b(-2;0;1). Зобразіть два довільних вектори. Побудуйте вектор, що дорівнює: а) сумі цих векторів; б) різниці цих векторів. Які властивості мають операції додавання та віднімання векторів? а с а с а + с

с=3а-0,5в, . a b 3a 0.5b с=3а-0,5в, с=3а-0,5в,

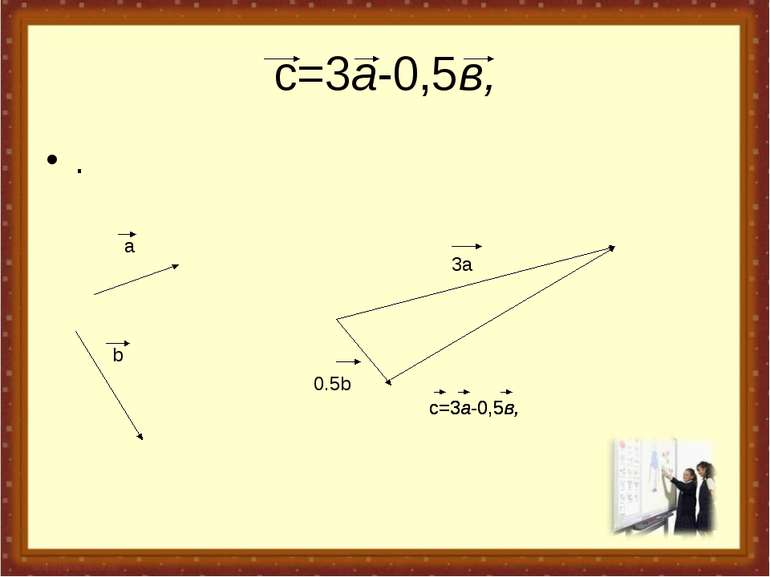
№10 Що називають добутком вектора на число? Які властивості має операція множення вектора на число? Знайдіть вектор с=3а-0,5в, якщо а(1;0;-1), в(0;-2;6).

№11 Які вектори називають колінеарними? Однаково напрямленими? Протилежно напрямленими? Рівними? Чи можуть протилежно напрямлені вектори бути неколінеарними? Сформулюйте умову колінеарності векторів. Чи колінеарні вектори: а) а(2;-1;3) і в(-4;2;-6); б) а(-1;2;-3) і в(-1;-4;-6)?

. №12 Сформулюйте означення кута між векторами у просторі. a b

№13 Що називають скалярним добутком векторів? Чому дорівнює скалярний добуток векторів а(2;-1;3) і в(-1;-2;1)? Які властивості має скалярний добуток векторів?

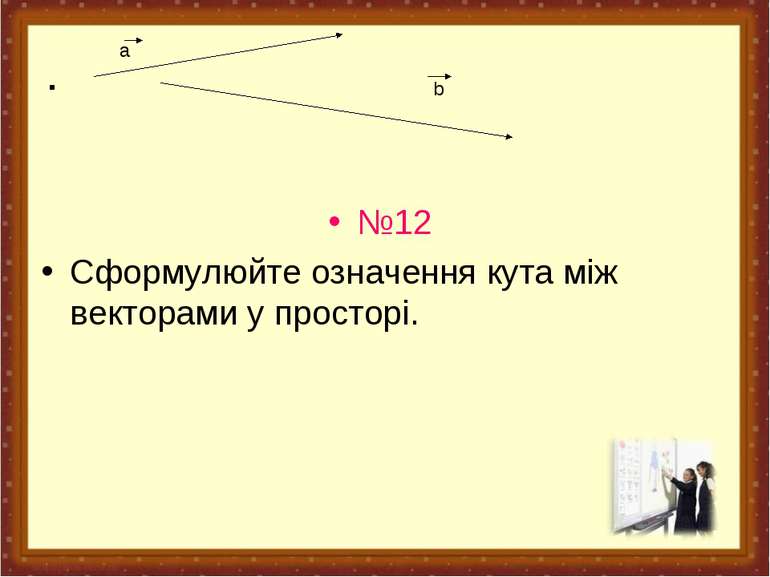
№14 За якою формулою можна знайти скалярний добуток векторів? Як, скориставшись цією формулою, знайти кут між векторами? Знайдіть кут між векторами а(3;1-;2) і в(1;2;3).

№15 Сформулюйте умову перпендикулярності векторів. При якому значенні n вектори а(3;-5; n) і в(2; n;-1) перпендикулярні? a b

Робота з підручником Ст123-125

Виконання контрольної роботи Перша частина - тестова (15 хвилин) Друга частина – виконання завдань в зошитах (25хвилин)

Підсумок уроку Ми закінчили вивчення теми:“ Координати та вектори в просторі”.

Домашнє завдання Повторити: кут між прямою і площиною; кут між площинами; перпендикулярність прямої і площини; теорему про три перпендикуляри; перпендикулярність площин.