Презентація на тему:
ДЕКАРТОВІ координати на площині і просторі

Підготувала вчителька математики Савельєва Ірина Олександрівна Березняківської загальноосвітньої школи Смілянського району

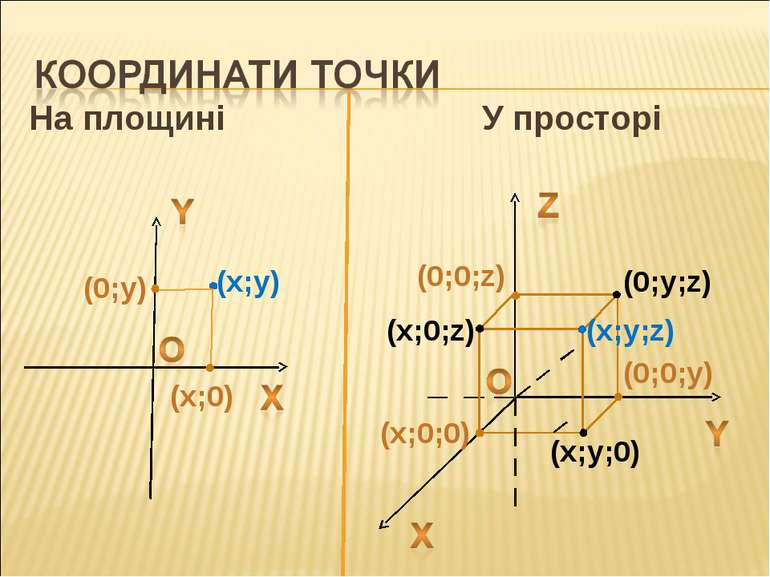
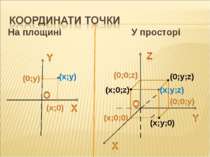
На площині У просторі (x;y) (x;y;0) (x;y;z) (x;0;0) (0;0;z) (0;y;z) (x;0;z) (0;0;y) (x;0) (0;y)

A(x1;y1) M (x1;y1;z1) На площині У просторі

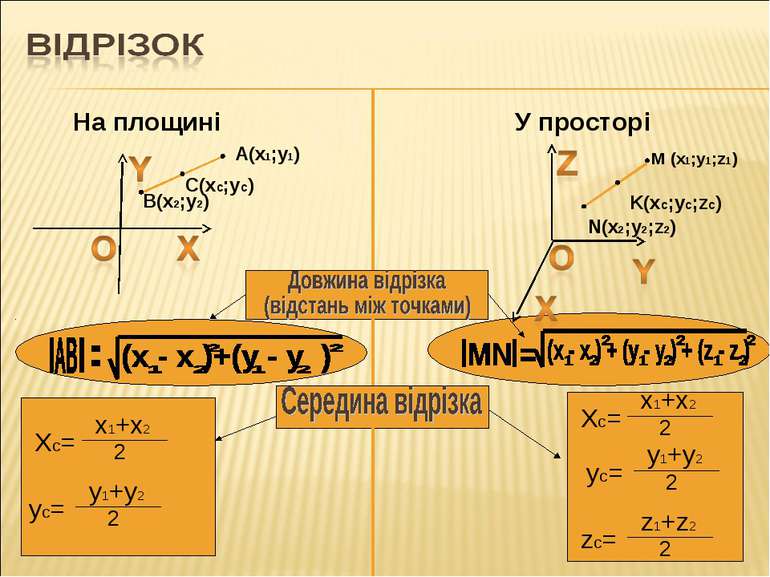
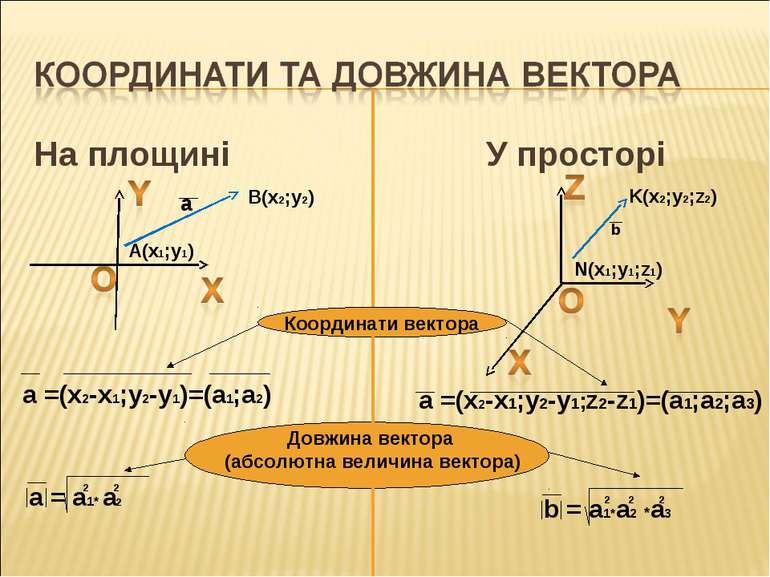
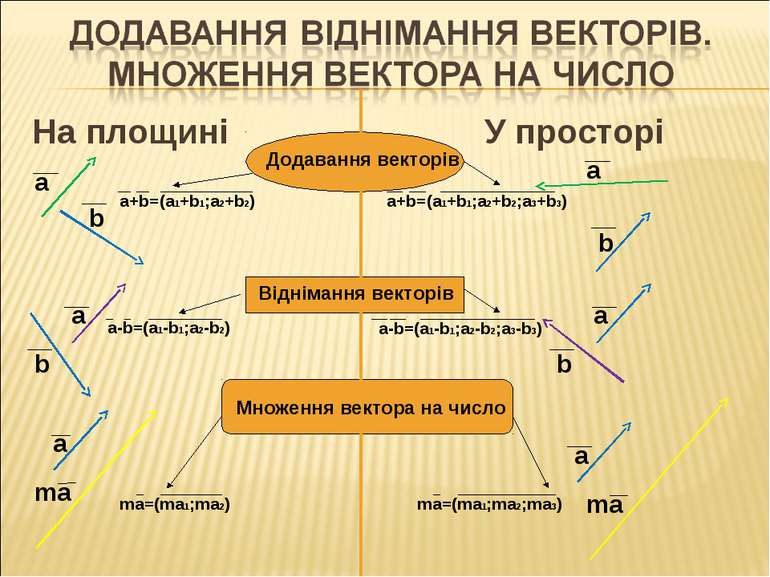
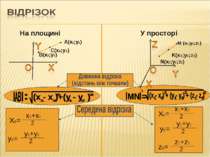
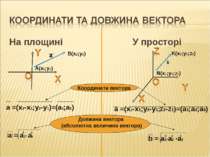
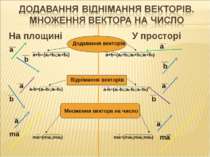
На площині У просторі N(x1;y1;z1) K(x2;y2;z2) B(x2;y2) A(x1;y1) Координати вектора Довжина вектора (абсолютна величина вектора) a =(x2-x1;y2-y1)=(a1;a2) a b a =(x2-x1;y2-y1;z2-z1)=(a1;a2;a3)

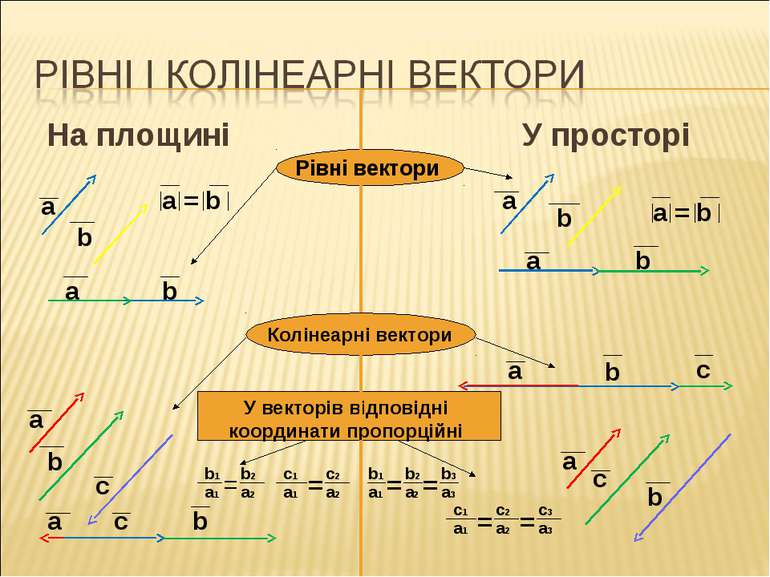
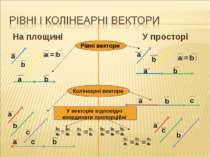
На площині У просторі Рівні вектори Колінеарні вектори У векторів відповідні координати пропорційні

На площині У просторі Додавання векторів Віднімання векторів Множення вектора на число

На площині У просторі Через координати Через кут між векторами ab=a1b1+a2b2+a3b3

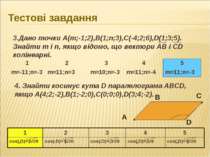
Тестові завдання Розв'яжи та виберіть правильну відповідь 1.Дано точки А(3;2;-1),В(0;-1;2),С(1;2;-4). Знайти точку D(x;y;z) таку, що АВ = СD. 2. Дано точку А(-1;7;2),В(-1;3;4),С(1;2;9). Знайти координати вектора m=АВ +2BС.

Розв'язок завдань Розв'язання 1) Рівні вектори мають рівні координати, тому знайдемо координати векторів АВ і СD. 2) Прирівняємо відповідні координати векторів АВ і СD і знайдемо невідомі. 3) Координати точки D. 1.Дано точки А(3;2;-1),В(0;-1;2),С(1;2;-4). Знайти точку D(x;y;z) таку, що АВ = СD. АВ(0 - 3; -1 - 2; 2 +1) = АВ(-3; - 3; 3). СD(х-1',у-2;z+4). -3=x-1, х = -2. -3=у-2, у = -1. 3=z+4, z=-1. D(-2;-1;-1). Відповідь: D(-2;-1;-1).

Розв'язок завдань Розв'язання 1) Знайдемо координати векторів АВ і ВС: 2) Знайдемо координати вектора 2ВС: 3) Знайдемо суму векторів АВ і 2ВС: 2. Дано точку А(-1;7;2),В(-1;3;4),С(1;2;9). Знайти координати вектора m=АВ +2BС. АВ(0;-4;2), ВС(2;-1;5). 2ВС = (2*2;-1*2;5*2); 2BC(4;-2;10). т =АВ + 2ВС =(0;- 4; 2) + (4; -2; 10) = (4; -6; 12). Відповідь: m=(4;-6;12).

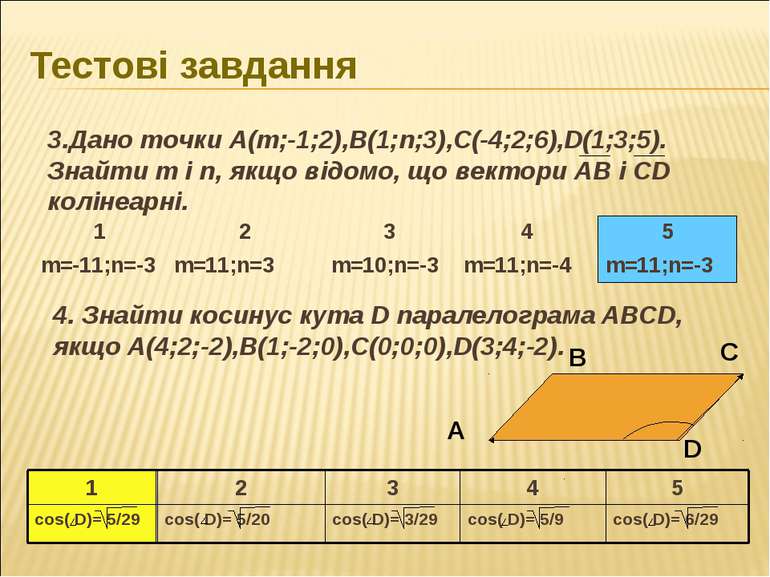
Тестові завдання 3.Дано точки А(m;-1;2),В(1;n;3),С(-4;2;6),D(1;3;5). Знайти m і n, якщо відомо, що вектори АВ і СD колінеарні. 4. Знайти косинус кута D паралелограма АВСD, якщо А(4;2;-2),В(1;-2;0),С(0;0;0),D(3;4;-2).

Розв'язок завдань Розв'язання 1) Знайдемо координати векторів МИ і РК: 2) Якщо вектори МИ і РК колінеарні, то їх координати пропорційні: 3.Дано точки А(m;-1;2),В(1;n;3),С(-4;2;6),D(1;3;5). Знайти m і n, якщо відомо, що вектори АВ і СD колінеарні. Відповідь : m = 11; n = -3

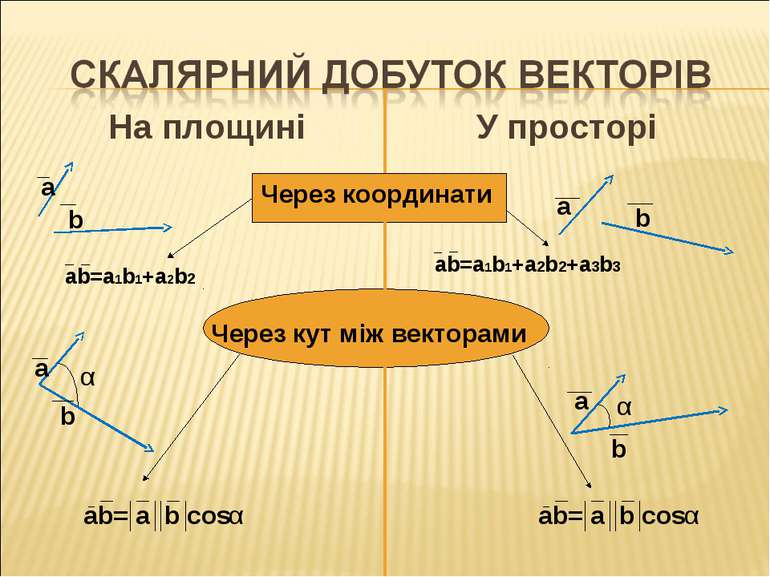
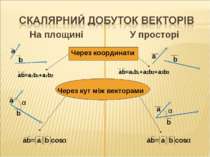
Розв'язок завдань 4. Знайти косинус кута D паралелограма АВСD, якщо А(4;2;-2),В(1;-2;0),С(0;0;0),D(3;4;-2). 1)Розглянемо паралелограм АВСD кут D утворений векторами DА і DС. 2)Знайдемо координати і абсолютні величини векторів DА і DС. 3)Знайдемо скалярний добуток DА і DС. 4)За формулою cos D =( a*b)/( a * b )маємо: Розв'язання D DA(1,-2,0); DA = 1+4+0 = 5 DC(-3;-4;2); DC = 9+16+4 = 29 DA*DC = (1;-2;0)*(-3;-4;2) = - 3+8+0 = 5 cos D = DA * DC = 5 = 5 DA * DC 5 * 29 29 Відповідь: cos D = 5 29

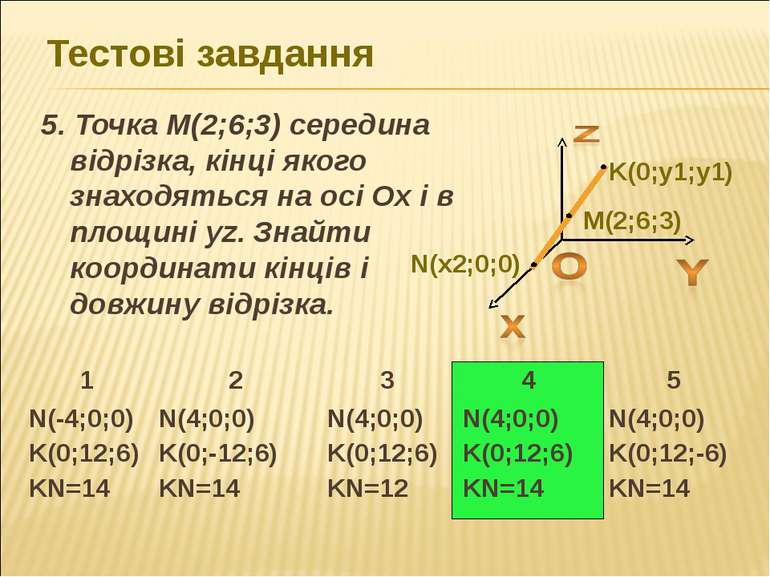
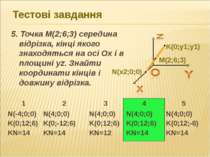
Тестові завдання 5. Точка M(2;6;3) середина відрізка, кінці якого знаходяться на осі Ох і в площині yz. Знайти координати кінців і довжину відрізка.

Розв'язок завдань 5. Точка M(2;6;3) середина відрізка, кінці якого знаходяться на осі Ох і в площині yz. Знайти координати кінців і довжину відрізка. Довільна точка, що лежить на осі Ох, має координати (х; 0; 0) ; довільна точка, що лежить у площині уz, має координати (0; у;z). Нехай точка М(2; 6; 3) є серединою відрізка, кінцями якого є точки А(х; 0; 0), B(0; у;z). Відповідь: A(4;0;0), B(0;12;6), AB = 14 Тоді: 2 = x+0 , 6 = 0+y , 3 = 0+z , 2 2 2 Звідки x = 4, y = 12, z = 6. Отримаємо А(4; 0; 0), B(0; 12;6), AB = (-4) + 12 + 6 = 14 2 2 2

Використана література 1.Чекова А.М. “Геометрія 7-12 класи”: навчальний посібник, - Х.: Країна мрій,2009.-120с. 2. Геометрія 9: підручник для загальноосвіт. навч.закл./ Г.В.Апостолова.- К.:Генеза,2009 – 304с. 3. Геометрія: Стереометрія: підручник для 10-11кл.серед.шк.-6-те вид. – К.: Освіта,2001. – 128с.